广东省深圳市罗湖区2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-20 类型:期中考试
一、单选题
-
1. 垃圾分类一小步,低碳生活一大步,垃圾桶上常有以下四种垃圾分类标识的图案和文字说明其中图案是中心对称图形的是( )A、
 有害垃圾
B、
有害垃圾
B、 厨余垃圾
C、
厨余垃圾
C、 其它垃圾
D、
其它垃圾
D、 可回收物
2. 若 , 则下列各式中不一定成立的是( )A、 B、 C、 D、3. 在平面直角坐标系中,有两点,则点C可由点D( )A、向上平移3个单位长度得到 B、向下平移3个单位长度得到 C、向左平移1个单位长度得到 D、向右平移1个单位长度得到4. 如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为( )
可回收物
2. 若 , 则下列各式中不一定成立的是( )A、 B、 C、 D、3. 在平面直角坐标系中,有两点,则点C可由点D( )A、向上平移3个单位长度得到 B、向下平移3个单位长度得到 C、向左平移1个单位长度得到 D、向右平移1个单位长度得到4. 如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为( )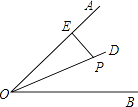 A、PN<3 B、PN>3 C、PN≥3 D、PN≤35. 下列命题是真命题的是( ).
A、PN<3 B、PN>3 C、PN≥3 D、PN≤35. 下列命题是真命题的是( ).
A、有两条边、一个角相等的两个三角形全等。 B、等腰三角形的对称轴是底边上的中线。 C、全等三角形对应边上的中线相等。 D、有一个角是60°的三角形是等边三角形。6. 如图,在中, , , 边的垂直平分线交于点E,交于点D,则的周长为( ) A、14 B、12 C、11 D、197. 如图,在△ABC中,AB=AC,直线l1∥l2 , 且分别与△ABC的两条边相交,若∠1=40°,∠2=23°,则∠C的度数为( )
A、14 B、12 C、11 D、197. 如图,在△ABC中,AB=AC,直线l1∥l2 , 且分别与△ABC的两条边相交,若∠1=40°,∠2=23°,则∠C的度数为( )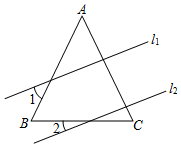 A、40° B、50° C、63° D、67°8. 如图△ABC中,AB=AC,∠BAC=120°,BC=2 ,D为BC的中点,DE⊥AB,则△EBD的面积为( )
A、40° B、50° C、63° D、67°8. 如图△ABC中,AB=AC,∠BAC=120°,BC=2 ,D为BC的中点,DE⊥AB,则△EBD的面积为( )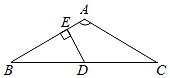 A、 B、 C、 D、9. 若关于x的一元一次不等式组有4个整数解,则m的取值范围为( )A、 B、 C、 D、10. 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
A、 B、 C、 D、9. 若关于x的一元一次不等式组有4个整数解,则m的取值范围为( )A、 B、 C、 D、10. 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠EDF;④AB+AC=2AE;
其中正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
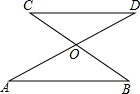
11. 若等腰三角形的一个底角是72°,则它的顶角是 .12. 如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是.
 13. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为.
13. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为.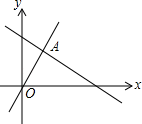 14. 如图,在中, , , , 将绕顶点O,按顺时针方向旋转到处,此时线段与的交点D恰好为的中点, , 则线段的长度为 .
14. 如图,在中, , , , 将绕顶点O,按顺时针方向旋转到处,此时线段与的交点D恰好为的中点, , 则线段的长度为 . 15. 如图,是边长为2的等边三角形,点P为直线上的动点,把线段绕A点逆时针旋转60°至 , O为边上一动点,则的最小值为 .
15. 如图,是边长为2的等边三角形,点P为直线上的动点,把线段绕A点逆时针旋转60°至 , O为边上一动点,则的最小值为 .
三、解答题
-
16.(1)、解不等式: , 并在数轴上表示其解集;(2)、解不等式组 , 并写出它的所有非负整数解.17. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形(顶点是网格线的交点).
 (1)、先将竖直向上平移6个单位,再水平向右平移3个单位得到 , 请画出;(2)、将绕点顺时针旋转90°,得 , 请画出;(3)、连接 , 直接写出的长 .18. 如图,在中, , , 将沿方向向右平移得到 .
(1)、先将竖直向上平移6个单位,再水平向右平移3个单位得到 , 请画出;(2)、将绕点顺时针旋转90°,得 , 请画出;(3)、连接 , 直接写出的长 .18. 如图,在中, , , 将沿方向向右平移得到 .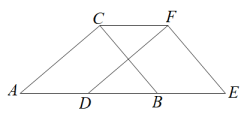 (1)、求的度数;(2)、若 , . 请求出的长度.19. 如图,直线AB∥CD,∠ACD的平分线CE交AB于点F,∠AFE的平分线交CA延长线于点G.
(1)、求的度数;(2)、若 , . 请求出的长度.19. 如图,直线AB∥CD,∠ACD的平分线CE交AB于点F,∠AFE的平分线交CA延长线于点G. (1)、证明:AC=AF;(2)、若∠FCD=30°,求∠G的大小.20. 如图,在△ABC中,AB=AC , 点D、E、F分别在AB、BC、AC边上,且BE=CF , BD=CE .
(1)、证明:AC=AF;(2)、若∠FCD=30°,求∠G的大小.20. 如图,在△ABC中,AB=AC , 点D、E、F分别在AB、BC、AC边上,且BE=CF , BD=CE .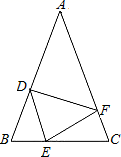 (1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数.21. 为了加强对校内外安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
(1)、求证:△DEF是等腰三角形;(2)、当∠A=40°时,求∠DEF的度数.21. 为了加强对校内外安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.甲型
乙型
价格(元/台)
a
b
有效半径(米/台)
150
100
(1)、求a、b的值;(2)、若购买该批设备的资金不超过11000元,且要求监控半径覆盖范围不低于1600米,两种型号的设备均要至少买一台,请你为学校设计购买方案,并计算最低购买费用.22. 如图1,在中, , , 把一块含30°角的三角板的直角顶点D放在的中点上(直角三角板的短直角边为 , 长直角边为),点C在上,点B在上. (1)、求重叠部分的面积;(2)、如图2,将直角三角板绕D点按顺时针方向旋转30度,交于点M,交于点N,①请说明;②在此条件下重叠部分的面积会发生变化吗?若发生变化,请求出重叠部分的面积,若不发生变化,请说明理由;(3)、如图3,将直角三角板绕D点按时针方向旋转(),交于点M,交于点N,则的结论仍成立吗?重叠部分得面积会变吗?(请直接写出结论不需说明理由)
(1)、求重叠部分的面积;(2)、如图2,将直角三角板绕D点按顺时针方向旋转30度,交于点M,交于点N,①请说明;②在此条件下重叠部分的面积会发生变化吗?若发生变化,请求出重叠部分的面积,若不发生变化,请说明理由;(3)、如图3,将直角三角板绕D点按时针方向旋转(),交于点M,交于点N,则的结论仍成立吗?重叠部分得面积会变吗?(请直接写出结论不需说明理由)