广东省汕头市潮南区2021-2022学年八年级下学期期中考试数学试卷(B)
试卷更新日期:2023-02-20 类型:期中考试
一、单选题
-
1. 下列二次根式中,与能合并的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 满足下列条件的三角形中,不是直角三角形的是( )A、三内角之比为1:2:3 B、三内角之比为3:4:5 C、三边长之比为3:4:5 D、三边长分别为1、、24. 在▱ABCD中,∠A=3∠B,则∠B的度数是( )A、30° B、36° C、45° D、60°5. 如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
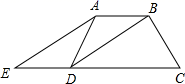
 A、3 B、 C、 D、6. 若 , 则代数式的值为( )A、2022 B、2004 C、 D、7. 如图,在 中, , , ,点D在边 上, , ,垂足为点F,交 于点E,则 的长为( )
A、3 B、 C、 D、6. 若 , 则代数式的值为( )A、2022 B、2004 C、 D、7. 如图,在 中, , , ,点D在边 上, , ,垂足为点F,交 于点E,则 的长为( ) A、2 B、 C、 D、8. 如图是由一串有公共点O的直角三角形演化而成的, , 那么的长为( )
A、2 B、 C、 D、8. 如图是由一串有公共点O的直角三角形演化而成的, , 那么的长为( ) A、 B、4 C、3 D、9. 如图,正方形ABCD的边长为2.对角线AC,BD交于点O,E为AC延长线上一点,且OE=2CO.则BE的长度是( )
A、 B、4 C、3 D、9. 如图,正方形ABCD的边长为2.对角线AC,BD交于点O,E为AC延长线上一点,且OE=2CO.则BE的长度是( ) A、 B、 C、 D、10. 将2021个形状、大小均相同的菱形按照如图所示的方式排成一列,使得右侧菱形的顶点与左侧菱形的对角线交点重合,若这些菱形的边长均为2,则阴影部分的周长总和等于( )
A、 B、 C、 D、10. 将2021个形状、大小均相同的菱形按照如图所示的方式排成一列,使得右侧菱形的顶点与左侧菱形的对角线交点重合,若这些菱形的边长均为2,则阴影部分的周长总和等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:;12. 在△ABC中,D,E分别是边AB,AC的中点,若DE=2,则BC= .13. 在平面直角坐标系中,矩形 的位置如图所示,其中 , 轴,则顶点D的坐标为.
 14. 三角形的三边长分别为2, , 3,则该三角形最长边上的中线长为15. 已知平面直角坐标系中,点P(2m-4,8)到坐标原点距离为10,则m的值为 .16. 如图,在中, , D,E分别是 , 的中点,连接 , , 若 , , 则点A到BC的距离是 .
14. 三角形的三边长分别为2, , 3,则该三角形最长边上的中线长为15. 已知平面直角坐标系中,点P(2m-4,8)到坐标原点距离为10,则m的值为 .16. 如图,在中, , D,E分别是 , 的中点,连接 , , 若 , , 则点A到BC的距离是 . 17. 如图,菱形ABCD中,O是两条对角线的交点,过点O的三条直线将菱形分成阴影部分和空白部分,当菱形的边长为5,一条对角线为8时,则阴影部分的面积为 .
17. 如图,菱形ABCD中,O是两条对角线的交点,过点O的三条直线将菱形分成阴影部分和空白部分,当菱形的边长为5,一条对角线为8时,则阴影部分的面积为 .
三、解答题
-
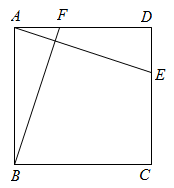
18. 计算:19. 先化简,再求值: , 其中 .20. 已知:如图,在矩形ABCD中,E、F分别是边CD、AD上的点, , 且 . 求证:矩形ABCD是正方形.
 21. 同学们在数学活动中研究了的性质:①;②;③ . 请你运用的性质解决下列问题:(1)、式子有意义,则x的取值范围;(2)、计算:的值;(3)、已知: , 求xy的值.22. 如图,某港口O位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,“远航”号每小时航行16海里,“海天”号每小时航行12海里.
21. 同学们在数学活动中研究了的性质:①;②;③ . 请你运用的性质解决下列问题:(1)、式子有意义,则x的取值范围;(2)、计算:的值;(3)、已知: , 求xy的值.22. 如图,某港口O位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,“远航”号每小时航行16海里,“海天”号每小时航行12海里. (1)、若它们离开港口一个半小时后分别位于A、B处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?说明理由.(2)、若“远航”号沿北偏东60°方向航行,经过两个小时后位于F处,此时船上有一名乘客需要紧急回到PE海岸线上,乘坐的快艇的速度是每小时80海里.他能在半小时内回到海岸线吗?说明理由.23. 如图,平行四边形ABCD中,∠ADB=90°.
(1)、若它们离开港口一个半小时后分别位于A、B处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?说明理由.(2)、若“远航”号沿北偏东60°方向航行,经过两个小时后位于F处,此时船上有一名乘客需要紧急回到PE海岸线上,乘坐的快艇的速度是每小时80海里.他能在半小时内回到海岸线吗?说明理由.23. 如图,平行四边形ABCD中,∠ADB=90°. (1)、求作:AB的垂直平分线MN,交AB于点M,交BD延长线于点N(要求:尺规作图,保留作图痕迹,不写作法,不下结论)(2)、在(1)的条件下,设直线MN交AD于E,且∠C=22.5°,求证:NE=AB.
(1)、求作:AB的垂直平分线MN,交AB于点M,交BD延长线于点N(要求:尺规作图,保留作图痕迹,不写作法,不下结论)(2)、在(1)的条件下,设直线MN交AD于E,且∠C=22.5°,求证:NE=AB.