广东省清远市清城区2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-20 类型：期中考试

进入出卷网下载

一、单选题

1. 节约资源，保护环境，人人有责．下列垃圾分类指引标志图形中，既是轴对称又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 若 $m > n$ ，则下列不等式正确的是（）

A、 $m - 6 < n - 6$ B、 $\frac{m}{6} > \frac{n}{6}$ C、 $6 m < 6 n$ D、 $- 6 m > - 6 n$

查看试题解析
3. 将点A（2，﹣1）向左平移4个单位长度得到点B，则点B的坐标是（）

A、（﹣2，﹣1） B、（6，﹣1） C、（2，3） D、（2，﹣5）

查看试题解析
4. 不等式3x-1＜8的解集是（　　）

A、x＞2 B、x＜3 C、x＜－1 D、x＜－2

查看试题解析
5. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ ，且 $B C = 4$ ，则BD长为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 下列等式中，从左到右的变形是因式分解的是（）

A、x（x-2）=x²-2x B、（x+1）²=x²+2x+1 C、x²-4=（x+2）（x-2） D、x²+2x+4=（x+1）²+3

查看试题解析
7. 已知一次函数 $y = k x + b$ 与 $y = m x + n$ 的图象如图所示，若 $k x + b > m x + n$ ，则x的取值范围为（）

A、 $x > 2$ B、 $x < 2$ C、 $x > - 2$ D、 $x < - 2$

查看试题解析
8. 如图在边长为a的正方形中挖掉一个边长为b的小正方形(a＞b)．把余下的部分剪拼成一个长方形，通过计算阴影部分的面积，验证了一个等式，则这个等式是（）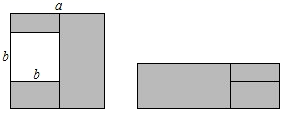

A、a²﹣2ab+b²＝(a﹣b)² B、a²﹣ab＝a(a﹣b) C、a²﹣b²＝(a﹣b)² D、a²﹣b²＝(a+b)(a﹣b)

查看试题解析
9. 如图， $R t Δ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ，交 $B C$ 于点 $D$ ， $A B = 10$ ， $S_{Δ A B D} = 15$ ，则 $C D$ 的长为（）

A、2 B、3 C、4 D、5

查看试题解析
10. 已知a，b，c分别是△ABC的三边长，若 $a^{2} + 2 a b + b^{2} = c^{2} + 24$ ， $a + b - c = 4$ ，则△ABC的周长是（）

A、3 B、6 C、8 D、12

查看试题解析

二、填空题

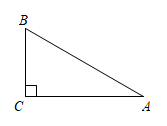
11. 把多项式 $a^{2} - 4 a$ 分解因式结果是．

查看试题解析
12. 如图，在△ABC中，∠C＝90°，∠A＝30°，AB＝6，则BC＝．

查看试题解析
13. 如图，将△ABC沿AC所在的直线平移到△DEF的位置，若图中AC＝10，DC＝6，则 $C F =$ ．

查看试题解析
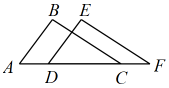14. 不等式4x-3≤2x+1的非负整数解的和是．

查看试题解析
15. 边长为a、b的长方形的周长为14，面积为6，则 $a^{2} b + a b^{2} =$ ．

查看试题解析
16. 如图，△ACB中，∠C＝90°，∠A＝30°，分别以点A，B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧交于点M，N，直线MN交AB于点E，交AC于点D．若CD＝3，则AD＝．

查看试题解析
17. 如图，△ABC为等边三角形，边长为6，AD⊥BC，垂足为点D，点E和点F分别是线段AD和AB上的两个动点，连接CE，EF，则BE＋EF的最小值为．

查看试题解析

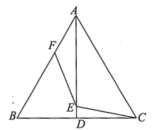
三、解答题

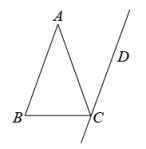
18. 因式分解：ab²﹣4ab+4a ．

查看试题解析
19. 解不等式组 ${\begin{array}{l} 3 x + 1 > x + 3 \\ \frac{1}{2} x - 1 \leq 0 \end{array}$ .

查看试题解析
20. 如图，在△ABC中，AB＝AC，∠A＝40°，CD∥BA，求∠BCD的度数．

查看试题解析
21. 如图，在平面直角坐标系中，△ABC的三个顶点分别是A（-2，-1），B（-4，-4），C（-1，-3）．

（ 1 ）把△ABC向右平移4个单位后得到对应的△A₁B₁C₁ ，请画出平移后的△A₁B₁C₁；

（ 2 ）把△ABC绕原点O旋转180°后得到对应的△A₂B₂C₂ ，请画出旋转后的△A₂B₂C₂；

（ 3 ）观察图形可知，△A₁B₁C₁与△A₂B₂C₂关于点（　　，　　）成中心对称．

查看试题解析
22. 已知△ABC的三边分别为a，b，c，且a＋b＝3，ab＝1， $c = \sqrt{7}$ ．

(1)、求 $a^{2} + b^{2}$ 的值；

(2)、试判断△ABC的形状，并说明理由．

查看试题解析
23. 学校近期举办了一年一度的经典诵读比赛.某班级因节目需要，须购买A、B两种道具.已知购买1件A道具比购买1件B道具多10元，购买2件A道具和3件B道具共需要45元.

(1)、购买一件A道具和一件B道具各需要多少元？

(2)、根据班级情况，需要这两种道具共60件，且购买两种道具的总费用不超过620元.求道具A最多购买多少件？

查看试题解析
24. 先阅读理解下面的例题，再按要求解答下列问题：
例题：解一元二次不等式 $x^{2} - 4 > 0$ ．
解 ∵ $x^{2} - 4 = (x + 2) (x - 2)$ ， ∴ $x^{2} - 4 > 0$ 可化为 $(x + 2) (x - 2) > 0$ ．
由有理数的乘法法则：两数相乘，同号得正，得
① ${\begin{array}{l} x + 2 > 0 \\ x - 2 > 0 \end{array}$ ② ${\begin{array}{l} x + 2 < 0 \\ x - 2 < 0 \end{array}$
解不等式组①，得 $x > 2$ ，解不等式组②，得 $x < - 2$ ，
∴ $(x + 2) (x - 2) > 0$ 的解集为 $x > 2$ 或 $x < - 2$ ，
即一元二次不等式 $x^{2} - 4 > 0$ 的解集为 $x > 2$ 或 $x < - 2$ ．

(1)、一元二次不等式 $x^{2} - 25 > 0$ 的解集为；

(2)、求使代数式 $\sqrt{2 x^{2} - 3 x}$ 有意义的x的取值范围；

(3)、试解不等式 $\frac{2 x - 1}{x - 4} \leq 0$ ．

查看试题解析
25. 如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形△AOB，点C为x轴正半轴上一动点（ $O C > 1$ ），连接BC，以线段BC为边在第四象限内作等边三角形△CBD，连接DA并延长，交y轴于点E．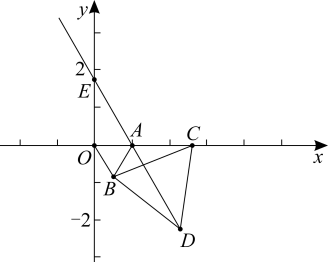

(1)、求证：△OBC≌△ABD．

(2)、在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数；如果变化，请说明理由．

(3)、以A，E，C为顶点的三角形是等腰三角形时，直接写出此时点C的坐标和CD的长度．

查看试题解析