广东省梅州市大埔县2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-20 类型:期中考试
一、单选题
-
1. 下列生态环保标志中,是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 已知 , 下列结论错误的是( )A、 B、 C、 D、3. 如图,在 和 中, ,添加一个条件,不能证明 和 全等的是( )
2. 已知 , 下列结论错误的是( )A、 B、 C、 D、3. 如图,在 和 中, ,添加一个条件,不能证明 和 全等的是( ) A、 B、 C、 D、4. 已知点与点关于x轴对称,则实数a,b的值是( )A、 , B、 , C、 , D、 ,5. 以下列线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )A、 , , B、 , , C、 D、 , ,6. 如图,在△ 中, ,将△ 绕点 顺时针旋转 ,得到△ ,连接 ,若 , ,则线段 的长为( )
A、 B、 C、 D、4. 已知点与点关于x轴对称,则实数a,b的值是( )A、 , B、 , C、 , D、 ,5. 以下列线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )A、 , , B、 , , C、 D、 , ,6. 如图,在△ 中, ,将△ 绕点 顺时针旋转 ,得到△ ,连接 ,若 , ,则线段 的长为( )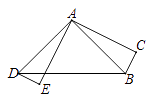 A、 B、 C、 D、7. 如图,在△ABC中, , 腰AB的垂直平分线交AB于点E,交BC于点D,若 , 则△ADC的周长为( )
A、 B、 C、 D、7. 如图,在△ABC中, , 腰AB的垂直平分线交AB于点E,交BC于点D,若 , 则△ADC的周长为( )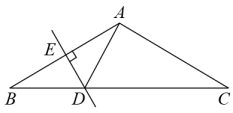 A、17cm B、18cm C、19cm D、无法计算8. 某品牌自行车进价是每辆800元,标价是每辆1200元,店庆期间,商场为了答谢顾客,进行打折促销活动,但是要保证利润率不低于5%,则最多可打( )折A、5 B、6 C、7 D、89. 在直角坐标系中,若点P(2x-6,x-5)在第四象限,则x的取值范围是( )A、3<x<5 B、-5<x<3 C、-3<x<5 D、-5<x<-310. 如图,的三边 , , 的长分别为 , , , 点O是三条角平分线的交点,则::等于( )
A、17cm B、18cm C、19cm D、无法计算8. 某品牌自行车进价是每辆800元,标价是每辆1200元,店庆期间,商场为了答谢顾客,进行打折促销活动,但是要保证利润率不低于5%,则最多可打( )折A、5 B、6 C、7 D、89. 在直角坐标系中,若点P(2x-6,x-5)在第四象限,则x的取值范围是( )A、3<x<5 B、-5<x<3 C、-3<x<5 D、-5<x<-310. 如图,的三边 , , 的长分别为 , , , 点O是三条角平分线的交点,则::等于( )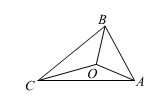 A、:: B、:: C、:: D、::
A、:: B、:: C、:: D、::二、填空题
-
11. 已知关于x的不等式x≥a-1的解集如图所示,则a的值为 .
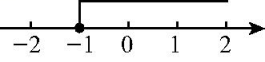 12. 等腰三角形的一个角等于40°,则它的顶角的度数是 .13. 在平面直角坐标系中,点A,B的坐标分别为 , , 将线段AB平移后,点A的对应点的坐标为 , 则点B的对应点的坐标为 .14. 如图,将△ABC绕着点C顺时针方向旋转50°后得到 . 若 , , 则的度数是 .
12. 等腰三角形的一个角等于40°,则它的顶角的度数是 .13. 在平面直角坐标系中,点A,B的坐标分别为 , , 将线段AB平移后,点A的对应点的坐标为 , 则点B的对应点的坐标为 .14. 如图,将△ABC绕着点C顺时针方向旋转50°后得到 . 若 , , 则的度数是 .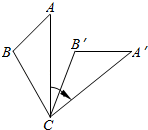 15. 如图,在△ABC中, , AD平分∠BAC,交BC于点D.若 , , 则△ABD的面积为 .
15. 如图,在△ABC中, , AD平分∠BAC,交BC于点D.若 , , 则△ABD的面积为 .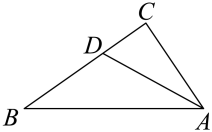 16. 一次函数与的图像如图所示,当x时, .
16. 一次函数与的图像如图所示,当x时, .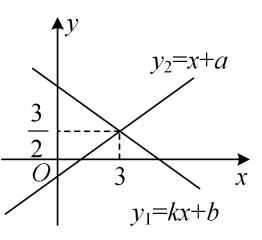 17. 下列命题中,其逆命题成立的是.(只填写序号)
17. 下列命题中,其逆命题成立的是.(只填写序号)①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c满足a2+b2=c2 , 那么这个三角形是直角三角形.
三、解答题
-
18. 解不等式19. 解不等式组.
请结合题意解答下列问题:
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式的解集在数轴上表示出来: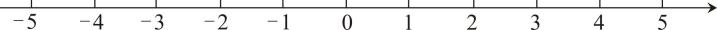 (4)、不等式组的解集为 .20. 在平面直角坐标系中,四边形ABCD的位置如图所示,解答下列问题:
(4)、不等式组的解集为 .20. 在平面直角坐标系中,四边形ABCD的位置如图所示,解答下列问题: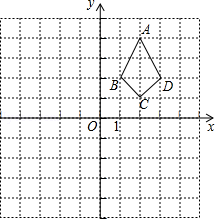
( 1 )将四边形ABCD先向左平移4个单位,再向下平移6个单位,得到四边形A1B1C1D1 , 画出平移后的四边形A1B1C1D1;
( 2 )将四边形A1B1C1D1绕点A1逆时针旋转90°,得到四边形A1B2C2D2 , 画出旋转后的四边形A1B2C2D2 , 并写出点C2的坐标.
21. 如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.你能说明BE与DF相等吗?请写出证明过程.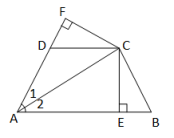 22. 在下列平面直角坐标系中画出函数y1=-x+3,y2=3x-4的图象.观察图象,回答下列问题:
22. 在下列平面直角坐标系中画出函数y1=-x+3,y2=3x-4的图象.观察图象,回答下列问题: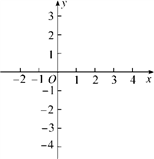 (1)、当x取何值时,y1=y2?(2)、当x取何值时,y1>y2?(3)、当x取何值时,y1<y2?23. 如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,将△ABC沿AB边所在直线向右平移3个单位,记平移后的对应三角形为△DEF,
(1)、当x取何值时,y1=y2?(2)、当x取何值时,y1>y2?(3)、当x取何值时,y1<y2?23. 如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,将△ABC沿AB边所在直线向右平移3个单位,记平移后的对应三角形为△DEF,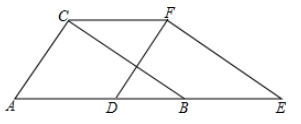 (1)、求DB的长;(2)、求此时梯形CAEF的面积.24. 去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.(1)、求饮用水和蔬菜各有多少件?(2)、现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;25. 甲、乙两台智能机器人从同一地点出发,沿着笔直的路线行走了450cm.甲比乙先出发,并且匀速走完全程,乙出发一段时间后速度提高为原来的2倍.设甲行走的时间为x(s),甲、乙行走的路程分别为y1(cm)、y2(cm),y1、y2与x之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)、求DB的长;(2)、求此时梯形CAEF的面积.24. 去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.(1)、求饮用水和蔬菜各有多少件?(2)、现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;25. 甲、乙两台智能机器人从同一地点出发,沿着笔直的路线行走了450cm.甲比乙先出发,并且匀速走完全程,乙出发一段时间后速度提高为原来的2倍.设甲行走的时间为x(s),甲、乙行走的路程分别为y1(cm)、y2(cm),y1、y2与x之间的函数图象如图所示,根据图象所提供的信息解答下列问题: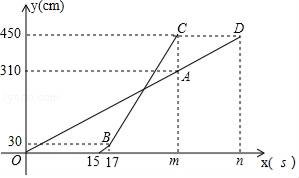 (1)、乙比甲晚出发s,乙提速前的速度是每秒cm,m= , n=;(2)、当x为何值时,乙追上了甲?(3)、在乙提速后到甲、乙都停止的这段时间内,当甲、乙之间的距离不超过20cm时,求x的取值范围.
(1)、乙比甲晚出发s,乙提速前的速度是每秒cm,m= , n=;(2)、当x为何值时,乙追上了甲?(3)、在乙提速后到甲、乙都停止的这段时间内,当甲、乙之间的距离不超过20cm时,求x的取值范围.