广东省茂名市茂南区2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个图案中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若a＜b，则下列各式中一定成立的是（　　）

A、﹣a＜﹣b B、2a＞2b C、a﹣1＜b﹣1 D、ac²＜bc²

查看试题解析
3. 将不等式组 ${\begin{array}{l} x > 1 \\ \frac{1}{3} x \leq 1 \end{array}$ 的解集在数轴上表示，正确的是（　　）

A、 B、 C、 D、

查看试题解析
4. 已知 $△ A B C$ 的三边为a，b，c，下列条件不能判定 $△ A B C$ 为直角三角形的是（）．

A、 $a = 3$ ， $b = 2$ ， $c = \sqrt{5}$ B、 $a = 40$ ， $b = 50$ ， $c = 60$ C、 $a = \frac{5}{4}$ ， $b = 1$ ， $c = \frac{3}{4}$ D、 $a = \sqrt{41}$ ， $b = 4$ ， $c = 5$

查看试题解析
5. 等腰三角形的一个内角是70°，则它的底角是（）

A、55° B、70° C、50°或70° D、70°或55°

查看试题解析
6. 将点P（-6，-9）向右平移1个单位，再向下平移2个单位后得到P′，则P′坐标为（　　）

A、（-6，-8） B、（-6，-11） C、（-5，-9） D、（-5，-11）

查看试题解析
7. 不等式 $3 x < 10 + x$ 的正整数解的个数为（）

A、 $5$ B、 $4$ C、 $3$ D、 $2$

查看试题解析
8. 下列命题中，它的逆命题成立的是（）

A、两条直线平行，内错角相等 B、全等三角形的对应角相等 C、如果两个实数相等，那么它们的绝对值相等 D、如果两个实数相等，那么它们的平方相等

查看试题解析
9. 如图，在△ABC中，分别以点A和点C为圆心，大于 $\frac{1}{2} A C$ 长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若 $A E = 4$ cm，△ABD的周长为13cm，则△ABC的周长为（）

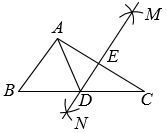A、17cm B、19cm C、21cm D、23cm

查看试题解析
10. 如图，将Rt△ABC沿着点B到点C的方向平移到△DEF的位置，已知 $A B = 6$ ， $H D = 2$ ， $C F = 3$ ，则图中阴影部分的面积为（）

A、12 B、15 C、18 D、24

查看试题解析

二、填空题

11. 已知 $M (a ， - 3)$ 和 $N (4 ， b)$ 关于原点对称，则a+b= ．

查看试题解析
12. 已知不等式组 ${\begin{array}{l} x > 1 \\ x < a - 1 \end{array}$ 无解，则a的取值范围为.

查看试题解析
13. 等腰三角形的底角必为锐角．用反证法证明，第一步是假设．

查看试题解析
14. 如图，OP平分∠AOB，P $C ⊥ O A$ 于点C，P $D ⊥ O B$ 于点D，若P $C =$ 2，则PD ．

查看试题解析
15. 如图是一次函数 $y_{1} = k x + b$ 与 $y_{2} = x + a$ 的图象，当x时， $y_{1} > y_{2}$ ．

查看试题解析
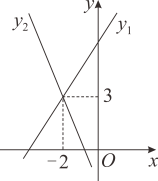16. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 15 °$ ， DE的垂直平分线AB分别交AB、BC于点D、E，连接AE，若 $B E = 6 c m$ ，则AC等于cm．

查看试题解析
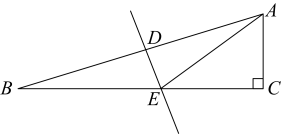17. 如图，已知△ABC中，∠C＝90°，AC＝BC $= \sqrt{2}$ ，将△ABC绕点A逆时针反向旋转60°到△AB′C′的位置，连接C′B，则C′B的长为．

查看试题解析

三、解答题

18. 解不等式： $\frac{x - 3}{2} - \frac{5 x - 1}{6} > - 2$ ，并把它的解集在数轴上表示出来．

查看试题解析
19. 解不等式组： ${\begin{array}{l} 3 x - 15 > 0 \\ 7 x - 2 < 8 x \end{array}$

查看试题解析
20. 如图，△ABC三个顶点的坐标分别是A（1，1），B（4，2），C（3，4）．
( 1 )若 $△ A B C$ 经过平移后得到 $△ A_{1} B_{1} C_{1}$ ，已知点 $C$ 的对应点 $C_{1}$ 的坐标为 $(- 2 ， 4)$ ，画出 $△ A_{1} B_{1} C_{1}$ ；
( 2 )请画出△ABC关于原点对称的△A₂B₂C₂ ．

查看试题解析
21. 如图，在△ABC中，AB＝AC，AD⊥BC于点D，E为AC边上一点，连接BE与AD交于点F，G为△ABC外一点，满足∠ACG＝∠ABE，∠FAG＝∠BAC，连接EG．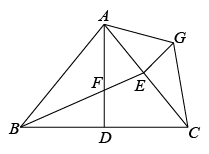

(1)、求证：△ABF≌△ACG；

(2)、求证：BE＝CG+EG．

查看试题解析
22. 已知：如图，△ABC中，∠BAC=90°，AB=AC，D为AC中点，F为BC上一点，AF⊥BD于E，

(1)、尺规作图：作∠BAC的角平分线交BD于G．（保留作图痕迹，不写做法，下结论）

(2)、求证：AG＝CF．

查看试题解析
23. 现代互联网技术的广泛应用，催生了快递行业的高速发展，经了解甲、乙两家快递公司比较合适，甲公司表示：快递物品不超过1千克的，收费16元；超过1千克，超过的部分按单价每千克2元收费．乙公司表示：快递物品不超过1千克的，收费10元；超过1千克，超过的部分按单价每千克4元收费．

(1)、设快递物品x千克（x>1），甲、乙公司收费分别为y_甲（元）和y_乙（元），分别写出甲、乙公司收费的表达式；

(2)、如果只考虑价格，不考虑其它因素，选择哪家快递公司更省钱？

查看试题解析
24. 2021年11月，我市政府紧急组织一批物资送往新冠疫情高风险地区，现已知这批物资中，食品和矿泉水共410箱，且食品比矿泉水多110箱．

(1)、求食品和矿泉水各有多少箱；

(2)、现计划租用A，B两种货车共10辆，一次性将所有物资送到群众手中，已知A种货车最多可装食品40箱和矿泉水10箱，B种货车最多可装食品20箱和矿泉水20箱，试通过计算帮助政府设计几种运输方案；

(3)、在（2）的条件下，A种货车每辆需付运费600元，B种货车每辆需付运费450元，政府应该选哪种方案，才能使运费最少？最少运费是多少？

查看试题解析
25. 如图，直线 $y = k x - 1$ （ $k > 0$ ）与x轴、y轴分别交于点B，C，且OB=2．

(1)、求k的值．

(2)、若点A是直线y=kx-1上一动点，且点A在第一象限，当△AOB的面积为2时，求点A的坐标．

(3)、在（2）的条件下，y轴上是否存在点P，使得△POA是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析