广东省茂名市2021-2022学年八年级下学期期中数学试卷
试卷更新日期:2023-02-20 类型:期中考试
一、单选题
-
1. 已知 , 则下列选项错误的是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在数轴上表示不等式﹣1<x2,其中正确的是( )A、
3. 在数轴上表示不等式﹣1<x2,其中正确的是( )A、 B、
B、 C、
C、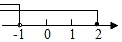 D、
D、 4. 如图,△ABC中,BC=14,边AB的垂直平分线和边AC的垂直平分线相交于点M,且与边BC分别相交于点D、E,连接AE、AD,则△AED的周长( )
4. 如图,△ABC中,BC=14,边AB的垂直平分线和边AC的垂直平分线相交于点M,且与边BC分别相交于点D、E,连接AE、AD,则△AED的周长( )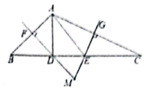 A、14 B、10 C、18 D、不能确定5. 如图,直线y=kx+b(b>0)经过点(2,0),则关于x的不等式kx+b>0的解集是( )
A、14 B、10 C、18 D、不能确定5. 如图,直线y=kx+b(b>0)经过点(2,0),则关于x的不等式kx+b>0的解集是( )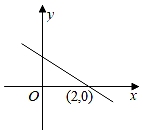 A、x>2 B、x<2 C、x≥2 D、x≤26. 已知点M(m,﹣1)与点N(3,n)关于原点对称,则m+n的值为( )A、3 B、2 C、﹣2 D、﹣37. 已知x=2不是关于x的不等式2x-m>4的整数解,x=3是关于x的不等式2x-m>4的一个整数解,则m的取值范围为( )A、0<m<2 B、0≤m<2 C、0<m≤2 D、0≤m≤28. 如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则AC的长是( )
A、x>2 B、x<2 C、x≥2 D、x≤26. 已知点M(m,﹣1)与点N(3,n)关于原点对称,则m+n的值为( )A、3 B、2 C、﹣2 D、﹣37. 已知x=2不是关于x的不等式2x-m>4的整数解,x=3是关于x的不等式2x-m>4的一个整数解,则m的取值范围为( )A、0<m<2 B、0≤m<2 C、0<m≤2 D、0≤m≤28. 如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则AC的长是( ) A、2 B、3 C、4 D、59. 如图,正方形的网格中,点A , B是小正方形的顶点,如果C点是小正方形的顶点,且使△ABC是等腰三角形,则点C的个数为( )
A、2 B、3 C、4 D、59. 如图,正方形的网格中,点A , B是小正方形的顶点,如果C点是小正方形的顶点,且使△ABC是等腰三角形,则点C的个数为( )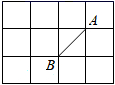 A、6 B、7 C、8 D、910. 如图,在Rt△ABC中, , , , 将△ABC绕点C按逆时针方向旋转得到 , 此时点恰好在AB边上,则点与点B之间的距离为( )
A、6 B、7 C、8 D、910. 如图,在Rt△ABC中, , , , 将△ABC绕点C按逆时针方向旋转得到 , 此时点恰好在AB边上,则点与点B之间的距离为( ) A、10 B、20 C、 D、
A、10 B、20 C、 D、二、填空题
-
11. 已知点在第二象限,则m的取值范围是 .12. 关于x的不等式组 , 则x的正整数解为 .13. 已知等腰三角形中的一个内角为100°,则这个等腰三角形的顶角为 .14. 如图,平移后得到 , 若 , , 则平移的距离的是 .
 15. 如图,在 中, , 平分 , 于D . 如果 ,那么 等于 .
15. 如图,在 中, , 平分 , 于D . 如果 ,那么 等于 . 16. 如图,将ABC绕点A逆时针旋转一定角度,得到ADE,若∠CAE=55°,∠E=70°,且AD⊥BC,则∠BAC的度数为 .
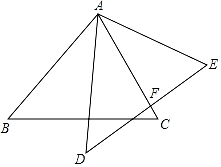
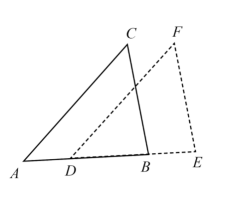
16. 如图,将ABC绕点A逆时针旋转一定角度,得到ADE,若∠CAE=55°,∠E=70°,且AD⊥BC,则∠BAC的度数为 . 17. 如图,在△ABC中,AB=4,BC=7,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为.
17. 如图,在△ABC中,AB=4,BC=7,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为.
三、解答题
-
18. 解不等式3x-1≤x+3,并把解在数轴上表示出来.
 19. 解下列不等式组: .20. 如图,在平面直角坐标系中,的三个顶点分别是 .
19. 解下列不等式组: .20. 如图,在平面直角坐标系中,的三个顶点分别是 .
( 1 )把向左平移个单位后得到对应的 , 请画出平移后的;
( 2 )把绕原点旋转后得到对应的 , 请画出旋转后的 .
21. 如图,P是内一点,于点A,于点B,连接 , . 求证:平分 .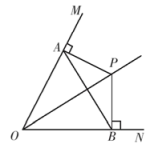 22. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,的三个顶点分别为 , , .
22. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,的三个顶点分别为 , , .
( 1 )画出关于原点对称的 , 并写出点的坐标;
( 2 )画出绕O点顺时针旋转后得到的 , 并写出点的坐标.