广东省江门市恩平市2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，最简二次根式是（）

A、 $\sqrt{27}$ B、 $\sqrt{6}$ C、 $\sqrt{\frac{1}{a}}$ D、 $\sqrt{3 a^{2}}$

查看试题解析
2. 下列四组数分别表示三角形的三条边长，其中能构成直角三角形的是(　　)

A、2、3、4 B、2、3、 $\sqrt{7}$ C、 $\sqrt{2}$ 、 $\sqrt{3}$ 、 $\sqrt{5}$ D、1、1、2

查看试题解析
3. 下列根式中，与 $\sqrt{2}$ 可合并的二次根式是(　　)

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{6}$ D、 $\sqrt{8}$

查看试题解析
4.
如图，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（　　）

A、3cm B、6cm C、9cm D、12cm

查看试题解析
5. 矩形具有而平行四边形不一定具有的性质是（）

A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分

查看试题解析
6. 下列计算正确的是(　　)

A、 $2 \sqrt{3} + 4 \sqrt{2} = 6 \sqrt{5}$ B、 $\sqrt{8} = 4 \sqrt{2}$ C、 $\sqrt{27} \div \sqrt{3} = 3$ D、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$

查看试题解析
7. 如图：四边形ABCD中，AD∥BC，下列条件中，不能判定ABCD为平行四边形的是(　　)

A、AD＝BC B、∠B+∠C＝180° C、∠A＝∠C D、AB＝CD

查看试题解析
8. 如图，RtΔABC中，AB=9，BC=6，∠B=90°，将ΔABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（）

A、 $\frac{5}{3}$ B、 $\frac{5}{2}$ C、4 D、5

查看试题解析
9. 已知菱形ABCD中，对角线AC与BD交于点O，∠BAD＝120°，AC＝4，则该菱形的周长是（）

A、 $16 \sqrt{3}$ B、16 C、 $8 \sqrt{3}$ D、8

查看试题解析
10. 如图，正方形 $A B C D$ 中，点E、F、H分别是 $A B$ 、 $B C$ 、 $C D$ 的中点， $C E$ 、 $D F$ 交于G，连接 $A G$ 、 $H G$ ，下列结论：① $C E ⊥ D F$ ；② $A G = A D$ ；③ $∠ C H G = ∠ D A G$ ；④ $H G = \frac{1}{2} A D$ ，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{x + 2}$ 有意义，则x的取值范围为．

查看试题解析
12. 化简： $\sqrt{48}$ ＝．

查看试题解析
13. 如图，在▱ABCD中，AB＝7，AD＝11，DE平分∠ADC，则BE＝．

查看试题解析
14. 如图，圆柱体的底面圆周长为 $8 c m$ ，高 $A B$ 为 $3 c m$ ， $B C$ 是上底面的直径，一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C，则爬行的最短路程为．

查看试题解析
15. 如图，已知平行四边形ABCD中，对角线AC⊥CD，∠D＝60°，E是AD的中点，连接CE，DC＝4，则平行四边形ABCD的面积是．

查看试题解析
16. 已知a、b、c是△ABC三边的长，且满足关系式 $\sqrt{c^{2} - a^{2} - b^{2}} + | a - b | = 0$ ，
则△ABC的形状为

查看试题解析
17. 如图，将折叠书架画出侧面示意图，AB面板架，CD为支撑架，EF为锁定杆，F可在CD上移动或固定，已知BC＝CE＝8cm，如图1，将面板AB竖直固定时（AB⊥BD），点F恰为CD的中点，如图2，当CF＝17cm，EF⊥AB，则底部BD＝cm，支撑架CD的长度为cm．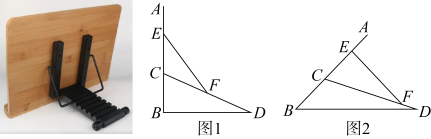

查看试题解析

三、解答题

18. 计算： $(\sqrt{12} + \sqrt{20}) + (\sqrt{3} - \sqrt{5})$ .

查看试题解析
19. 如图，四边形ABCD是平行四边形，点E在BC上，点F在AD上，BE＝DF．求证：AE＝CF．

查看试题解析
20. 如图，在离水面高8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，此人以1米每秒的速度收绳，7秒后船移动到点D的位置，问此时船与岸边的距离比原来近了多少米？（假设绳子是直的）

查看试题解析
21. 化简求值： $\frac{a^{2} - 1}{a^{2} - 2 a + 1} + \frac{2 a - a^{2}}{a - 2} \div a$ ，其中 $a = \sqrt{2} + 1$ ；

查看试题解析
22. 如图，在 $△ A B C$ 中，AB＝AC，BC＝15，D是AB上一点，BD＝9，CD＝12，求AC长．

查看试题解析
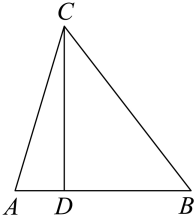23. 如图，菱形ABCD的两条对角线AC和BD相交于点O，并且 $D E ∥ O C$ ， $C E ∥ O D$ ．

(1)、求证：四边形OCED是矩形；

(2)、若 $A C = 4 \sqrt{5}$ ， $B D = 2 \sqrt{5}$ ，求矩形OCED的周长与面积．

查看试题解析
24. 有这样一类题目：将 $\sqrt{a \pm 2 \sqrt{b}}$ 化简，如果你能找到两个数m、n，使 $m^{2} + n^{2} = a$ 且 $m n = \sqrt{b}$ ， $a \pm 2 \sqrt{b}$ 将变成 $m^{2} + n^{2} \pm 2 m n$ ，即变成 $(m \pm n)^{2}$ ，从而使 $\sqrt{a \pm 2 \sqrt{b}}$ 得以化简．

(1)、例如，∵ $5 + 2 \sqrt{6} = 3 + 2 + 2 \sqrt{6} = (\sqrt{3})^{2} + (\sqrt{2})^{2} + 2 \sqrt{2} \times \sqrt{3} = (\sqrt{3} + \sqrt{2})^{2}$ ，
∴ $\sqrt{5 + 2 \sqrt{6}} = \sqrt{(\sqrt{3} + \sqrt{2})^{2}} =$ ，请完成填空．

(2)、仿照上面的例子，请化简 $\sqrt{4 - 2 \sqrt{3}}$ ；

(3)、利用上面的方法，设 $A = \sqrt{6 + 4 \sqrt{2}}$ ， $B = \sqrt{3 - \sqrt{5}}$ ，求A＋B的值．

查看试题解析
25. 如（图1），矩形OABC的边OA、OC在坐标轴上，点A坐标为（5，0），点C坐标为（0，3）点P是射线BA上的一动点，把矩形OABC沿着CP折叠，点B落在点D处；

(1)、填空：点B坐标为；

(2)、如图1，当点C，D，A共线时，AD＝；

(3)、如（图2），当点P与点A重合时，CD与x轴交于点E，过点E作EF⊥AC，交BC于点F，请判断四边形CEAF的形状，并说明理由．

查看试题解析