广东省河源市紫金县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-20 类型：期中考试

进入出卷网下载

一、单选题

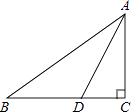
1. 若等腰三角形的两边长分别是2和10，则它的周长是（　　）

A、14 B、22 C、14或22 D、12

查看试题解析
2. 下列各组数中，不能够作为直角三角形的三边长的是（　　）

A、3，4，5 B、5，12，13 C、6，8，10 D、1，2，3

查看试题解析
3. 如图，在Rt△ABC中，∠A＝90°，∠ABC的平分线BD交AC于点D，AD＝2，BC＝7，则△BDC的面积是（）

A、2 B、7 C、9 D、14

查看试题解析
4. 如图，若记北京为 $A$ 地，莫斯科为 $B$ 地，雅典为 $C$ 地．若想建立一个货物中转仓，使其到 $A$ 、 $B$ 、 $C$ 三地的距离相等，则中转仓的位置应选在（）

A、三边垂直平分线的交点 B、三边中线的交点 C、三条角平分线的交点 D、三边上高的交点

查看试题解析
5. 给出下列各式：① $- 3 < 0$ ；② $a + b$ ；③ $x = 5$ ；④ $x^{2} - x y + y^{2}$ ；⑤ $x + 2 > y - 7$ ；⑥ $a \neq 3$ ．其中不等式的个数是（　　）

A、5 B、2 C、3 D、4

查看试题解析
6. 如图，△ABC是等边三角形，点E是AC的中点，过点E作EF⊥AB于点F，延长BC交EF的反向延长线于点D，若EF=1，则DF的长为（）

A、2 B、2.5 C、3 D、3.5

查看试题解析
7. 不等式 $- 2 x < 6$ 的非正整数解有（）

A、1个 B、2个 C、3个 D、无数多个

查看试题解析
8. 设 $a < b$ ，则下面不等式正确的是（）

A、 $- 2 a < - 2 b$ B、 $2 - a < 2 - b$ C、 $\frac{a}{3} + 1 < \frac{b}{3} + 1$ D、 $3 a - 3 > 3 b - 3$

查看试题解析
9. 如图，将 $△ A B C$ 绕点A按逆时针方向旋转110°，得到 $△ A B^{'} C^{'}$ ，若点 $B^{'}$ 在线段BC的延长线上，则 $∠ B B^{'} C^{'}$ 的度数为（）

A、65° B、70° C、75° D、80°

查看试题解析
10. 若 $x^{2} + m x - 15 = (x + 3) (x + n)$ ，则 $m$ 的值为（）

A、 $- 5$ B、 $5$ C、 $- 2$ D、 $2$

查看试题解析

二、填空题

11. 当x时， $- 2 x \leq 3 x$ ．

查看试题解析
12. 已知点 $B (1 ， - 3)$ 是由点A先向上平移4个单位，再向左平移3个单位得到的，则点A的坐标是．

查看试题解析
13. 分解因式： $m^{2} - 2 m - 8 =$ ．

查看试题解析
14. 等腰三角形有一个外角是110°，则这个等腰三角形的顶角度数为．

查看试题解析
15. 在直角△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若CD=4，则点D到斜边AB的距离为．

查看试题解析
16. 直线l₁：y＝x+1与直线l₂：y＝mx+n相交于点P（a，2），则关于x的不等式x+1≥mx+n的解集为．

查看试题解析
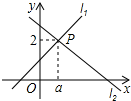17. 关于x的不等式组 ${\begin{array}{l} 2 x + 1 > 3 \\ a - x > 1 \end{array}$ 的解集为1＜x＜3，则a的值为．

查看试题解析

三、解答题

18. 已知△ABC在平面直角坐标系中的位置如图所示．

(1)、画出△ABC关于原点O对称的△A₁B₁C₁；

(2)、直接写出A₁ ， B₁ ， C₁三点的坐标．

查看试题解析
19. 解不等式组 ${\begin{array}{l} 3 x < x + 8 \\ 4 (x + 1) \leq 7 x + 10 \end{array}$ ，并把解集表示在数轴上．

查看试题解析
20. 如图， $△ ABO$ 与 $△ CDO$ 关于O点中心对称，点E、F在线段AC上，且AF=CE．
求证：FD=BE．

查看试题解析
21. 如图，在 $△$ ABC中，DE垂直平分BC，垂足为E，交AC于点D，连接BD．若∠A=100°，∠ABD=22°，求∠C的度数．

查看试题解析
22. 已知 $x + y = 1$ ，求 $\frac{1}{2} x^{2} + x y + \frac{1}{2} y^{2}$ 的值．

查看试题解析

23. 某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调，如表是近两周的销售情况：

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	3台	5台	18000元
第二周	4台	10台	31000元

(进价、售价均保持不变，利润＝销售总收入进货成本)

(1)、求A、B两种型号的空调的销售单价；

(2)、若超市准备用不多于54000元的金额再采购这两种型号的空调共30台，求A种型号的空调最多能采购多少台？

查看试题解析

24. 如图，已知AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，BE＝CF.

(1)、求证：△ABC是等腰三角形；

(2)、若AB＝5，BC＝6，求DE的长.

查看试题解析
25. “中国人的饭碗必须牢牢掌握在咱们自己手中．”为扩大粮食生产规模，某粮食生产基地计划投入一笔资金购进甲、乙两种农机具．已知购进2件甲种农机具和1件乙种农机具共需3.5万元，购进1件甲种农机具和3件乙种农机具共需3万元．

(1)、购进1件甲种农机具和1件乙种农机具各需多少万元？

(2)、若该粮食生产基地计划购进甲、乙两种农机具共10件，且投入资金既不少于9.8万元又不超过12万元，有哪几种购买方案？

(3)、在（2）的条件下，哪种购买方案需要的资金最少，最少资金是多少？

查看试题解析