广东省广州市越秀区2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-20 类型：期中考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{x + 3}$ 有意义，则x的取值范围是（　　）

A、x＞-3 B、x＜-3 C、x≥-3 D、x≤-3

查看试题解析
2. 下列计算结果正确的是（　　）

A、 $\sqrt{8}$ + $\sqrt{2}$ ＝ $\sqrt{10}$ B、 $\sqrt{8}$ - $\sqrt{2}$ ＝ $\sqrt{2}$ C、 $\sqrt{8}$ × $\sqrt{2}$ ＝ $\sqrt{16}$ D、 $\sqrt{8}$ ÷ $\sqrt{2}$ ＝ $\sqrt{4}$

查看试题解析
3. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，E是AB的中点，连接 $O E$ ，若 $O E = 3$ cm，则 $A D$ 的长为（）

A、3cm B、6cm C、9cm D、12cm

查看试题解析
4. 下列二次根式能与 $\sqrt{2}$ 合并的的是（　　）

A、 $\sqrt{12}$ B、 $\sqrt{24}$ C、 $\sqrt{27}$ D、 $\sqrt{98}$

查看试题解析
5. 如图所示，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为（）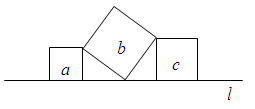

A、4 B、6 C、16 D、55

查看试题解析
6. 下列命题中，假命题是（　　）

A、若三角形的三边a、b、c满足a＝ $\sqrt{2}$ ， b＝1，c＝l，则这个三角形是直角三角形； B、在Rt $△$ ABC中∠C＝90°，∠C所对的边为c，其余两边为a、b，则有a²+b²＝c²； C、如果一个三角形的三个角满足∠A：∠B：∠C＝1：2：3，则 $△$ ABC是直角三角形； D、在直角三角形中两边的平方和等于第三边的平方

查看试题解析
7. 下列给出的条件能判定四边形 $A B C D$ 为平行四边形的是（）

A、AB//CD， $A D = B C$ B、 $∠ A = ∠ B$ ， $∠ C = ∠ D$ C、 $A B = C D$ ， $A D = B C$ D、 $A B = A D$ ， $C B = C D$

查看试题解析
8. 如图，在菱形ABCD中，对角线AC与BD相交于点O，且AC＝12，BD＝16，则菱形的高AE为（）

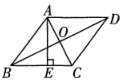A、9.6 B、4.8 C、10 D、5

查看试题解析
9. 在平面直角坐标系xOy中，已知A(1，-1)，B(4，2)，C(0，3)，下列坐标不能与A、B、C构成平行四边形的是（　　）

A、(-3，0) B、(5，-2) C、(3，6) D、(-3，-2)

查看试题解析
10. 如图，已知AC＝BC，∠ACB＝90°，∠ADC＝45°，AD⊥BD，BD＝2，CD＝3 $\sqrt{2}$ ，则AB长为（　　）

A、3 $\sqrt{2}$ B、2 $\sqrt{17}$ C、 $\sqrt{22}$ D、 $\sqrt{34}$

查看试题解析

二、填空题

11. 化简 $\sqrt{\frac{5}{6}}$ ＝．

查看试题解析
12. 命题“邻边相等的矩形是正方形”的逆命题是．

查看试题解析
13. 若1＜x＜2，则 $\sqrt{(x - 2)^{2}}$ 的值为．

查看试题解析
14. 如图，在平行四边形ABCD中，AE平分∠BAD，交CD边于E，AD＝3，EC＝2，则AB的长为．

查看试题解析
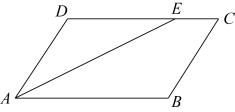15. 如图，将一根长为24cm的筷子置于底面直径为12cm，高为16cm的圆柱形水杯中，则筷子露在杯子外面的（h的长度）最短长度为cm．

查看试题解析
16. 如图，分别以Rt $△$ ABC的直角边AC，斜边AB为边向外作等边 $△$ ACD和 $△$ ABE，F为AB的中点，连接DF、EF，∠ACB＝90°，∠ABC＝30°，则以下4个结论：①AC⊥DF；②四边形BCDF为平行四边形；③DA+DF＝BE；④ $S_{△ A C D} ：$ S_四_边_形BCDE＝1：7，中正确的是．

查看试题解析

三、解答题

17. 计算：

(1)、 $3 \sqrt{6} + \sqrt{2} - 2 \sqrt{6} - 3 \sqrt{2}$ ．

(2)、 $(\sqrt{3} - 1)^{2} + (3 - \sqrt{3}) (2 + \sqrt{3})$ ．

查看试题解析
18. 如图，E、F是平行四边形 $A B C D$ 对角线 $B D$ 上的两点，且 $B E = D F$ .求证：四边形 $A E C F$ 是平行四边形.

查看试题解析
19. 已知：|a- $\sqrt{7}$ -2|+ $\sqrt{b - 2}$ ＝0，求a²-2ab+b²的值．

查看试题解析
20. 如图所示， $A B = 6$ ， $B C = 8$ ， $A D = 24$ ， $C D = 26$ ， $∠ B = 90 °$ ，求阴影部分的面积.

查看试题解析
21. 如图，小亮发现升旗的绳子放下时，末端刚好接触到地面 $E$ 处，但将绳子末端拉到距离旗杆 $8$ 米的 $B$ 处，发现此时绳子末端距离地面 $2$ 米.求旗杆的高度.

查看试题解析
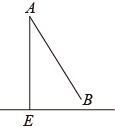22. 如图，已知四边形ABCD是矩形，两条对角线AC、BD相交于O，且AE $∥$ BD，DE $∥$ AC．

(1)、试判断四边形AODE的形状，并说明理由；

(2)、若BC＝4，AC＝6，求四边形AODE的面积．

查看试题解析
23. 如图，已知等边 $△$ ABC中，BE、CD分别是AC、AB边上的中线，BE、CD相交于点O，点M、N分别为线段OB和OC中点．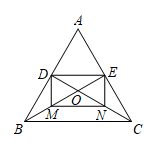

(1)、求证：四边形DENM是矩形；

(2)、若等边 $△$ ABC的边长为12，求矩形DENM的面积．

查看试题解析
24. 如图，矩形ABCD中，E是AD的中点，将 $△$ ABE沿BE折叠后得到 $△$ GBE，且G点在矩形ABCD内部，延长BG交DC于点F．

(1)、求证：GF＝DF；

(2)、若DC＝9，DE＝2CF，求AD的长；

(3)、若DC＝n•DF，那么n• $\frac{A D^{2}}{A B^{2}}$ 是否为定值？若是，求出这个定值；若不是，请说明理由．

查看试题解析
25. 如图，在正方形ABCD中，P是对角线BD上一点，点E在AB的延长线上，且PC＝PE．

(1)、求证：PA＝PE；

(2)、求证：AE＝ $\sqrt{2}$ DP；

(3)、若已知正方形的边长为2，求CP+ $\frac{1}{2}$ BP的最小值．

查看试题解析