北京市通州区2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-02-20 类型：期中考试

进入出卷网下载

一、

1. 点P（-2，3），在（）象限．

A、第一 B、第二 C、第三 D、第四

查看试题解析
2. 如果一个多边形的内角和是其外角和的两倍，那么这个多边形是（　　）

A、六边形 B、五边形 C、四边形 D、三角形

查看试题解析
3. 在平面直角坐标系中，x轴上一点P到y轴的距离是2，则点P的坐标是（　　）

A、（0，2） B、（2，0） C、（-2，0） D、（-2，0）或（2，0）

查看试题解析
4. 点 $(- 1 ， 4)$ 关于坐标原点对称的点的坐标是（）

A、 $(- 1 ， - 4)$ B、 $(1 ， - 4)$ C、 $(1 ， 4)$ D、 $(4 ， - 1)$

查看试题解析
5. 如图，在▱ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，若AB＝6，EF＝2，则BC的长为（）

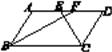A、8 B、10 C、12 D、14

查看试题解析
6. 甲无人机从地面起飞，乙无人机从距离地面20m高的楼顶起飞，两架无人机同时匀速上升10s．甲、乙两架无人机所在的位置距离地面的高度y（单位：m）与无人机上升的时间x（单位：s）之间的关系如图所示．下列说法正确的是（）

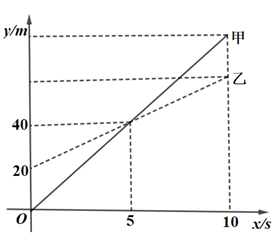A、5s时，两架无人机都上升了40m B、10s时，两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时，甲无人机距离地面的高度是60m

查看试题解析
7. 如图，正五边形的五个内角都相等，五条边都相等，连接对角线 $A D$ ， $B E$ ， $C E$ ，线段 $A D$ 分别与 $B E$ 和 $C E$ 相交于点M，N．下列结论：① $∠ A M E = 108 °$ ；② $A N = A E$ ；③ $∠ E B C = 2 ∠ B E C$ ，其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 $y = k_{n} x + b_{n} (n = 1 ， 2 ， 3 ， 4 ， 5 ， 6 ， 7)$ ，其中 $k_{1} = k_{2} ， b_{3} = b_{4} = b_{5}$ ，则他探究这7条直线的交点个数最多是（）

A、17个 B、18个 C、19个 D、21个

查看试题解析

二、填空题

9. 洞庭湖地区连日遭到暴雨袭击，导致湖水水位猛涨．如图是涨水期 $22$ 日 $- 27$ 日的水位记录，请你观察图像．
写出2条你观察图像后得到的正确信息，．

查看试题解析
10. 已知函数 $y = k x$ 经过二、四象限，且函数不经过 $(- 1 ， 1)$ ，请写出一个符合条件的函数解析式．

查看试题解析
11. 如图所示，四边形 $A B C D$ 是平行四边形，点E在线段 $B C$ 的延长线上，若 $∠ D C E = 132 °$ ，则 $∠ A =$ ．

查看试题解析
12. 如图，在四边形 $A B C D$ 中， $A E ⊥ B D$ ， $C F ⊥ B D$ ，垂足分别为点E，F．请你只添加一个条件（不另加辅助线），使得四边形 $A E C F$ 为平行四边形，你添加的条件是．

查看试题解析
13. 如图，点A、B、C、D、E在同一平面内，连接 $A B$ 、 $B C$ 、 $C D$ 、 $D E$ 、 $E A$ ，若 $∠ A B C = 130 °$ ，则 $∠ A + ∠ C + ∠ D + ∠ E =$ ．

查看试题解析
14. 如图， $▱ A B C D$ 的顶点A，B，C的坐标分别是 $(0 ， 1)$ ， $(- 2 ， - 2)$ ， $(2 ， - 2)$ ，则顶点D的坐标是．

查看试题解析
15. 已知函数y＝ ${\begin{matrix} x^{2} ， 0 \leq x < 1 \\ 2 x - 2 ， x \geq 1 \end{matrix}$ ，若y＝2，则x＝.

查看试题解析
16. 如图，在平面直角坐标系中，函数 $y = 2 x$ 和 $y = - x$ 的图象分别为直线 $l_{1}$ ， $l_{2}$ ，过点（1，0）作x轴的垂线交 $l_{1}$ 于点 $A_{1}$ ，过点 $A_{1}$ 作 $y$ 轴的垂线交 $l_{2}$ 于点 $A_{2}$ ，过点 $A_{2}$ 作x轴的垂线交 $l_{1}$ 于点 $A_{3}$ ，过点 $A_{3}$ 作 $y$ 轴的垂线交 $l_{2}$ 于点 $A_{4}$ ， …，依次进行下去，点 $A_{2022}$ 的坐标为．

查看试题解析

三、解答题

17. 已知一次函数 $y = k x + b (k \neq 0)$ ，当 $x = 3$ 时， $y = - 7$ ，当 $x = - 5$ 时， $y = 1$ ，求一次函数解析式．

查看试题解析
18. 如图，四边形 $A B C D$ 中， $∠ B = ∠ D$ ， $E F$ 交 $C D$ 于点G，交 $A D$ 于点E，交 $B C$ 的延长线于点F， $∠ D E F = ∠ C F$ ．求证：四边形 $A B C D$ 是平行四边形．

查看试题解析
19. 某文具店促销一种圆珠笔，它的单价随购买量的增加而降低，购买量，单价分为四个档，具体方案如下：购买 $1 ～ 5$ 支，每支售价1.0元；购买 $6 ～ 10$ 支，超出 $5$ 支的部分按照每支0.9元销售；购买 $11 ～ 20$ 支，超过 $10$ 支的部分按照每支 $0.8$ 元销售；购买 $21$ 支及以上，超出 $20$ 支的部分按照每支 $0.7$ 元销售．请你分别写出顾客购买这种圆珠笔时付款总额（y）元与他购买的数量（x）支之间的函数关系式，并写出自变量的取值范围．

查看试题解析
20. 如图，一次函数 $y = - \frac{3}{4} x + 3$ 图像与x轴，y轴分别交于点M、N，点C是第一象限内的点，且满足 $∠ N M C = 90 °$ ， $△ M N C$ 是等腰直角三角形．

(1)、求点M，N坐标；

(2)、求 $△ M N C$ 的面积．

查看试题解析
21. 已知四边形 $A B C D$ 是平行四边形，对角线 $A C$ ， $B D$ 相交于点O，直线 $E F$ 过点O，交 $A D$ 于点E，交 $B C$ 于点F，连接 $A F$ ， $C E$ ．

(1)、补全图形；

(2)、求证：四边形 $A F C E$ 是平行四边形．

查看试题解析
22. 如图，在平面直角坐标系 $x O y$ 中，函数 $y = - 2 x + 6$ 的图像分别交x轴，y轴于A，B两点，过点A的直线交y轴正半轴于点M，且BM=2MO．在平面直角坐标系内存在点C，使得以A，B，M，C为顶点的四边形是平行四边形，请你画出图形，确定点C的坐标．

查看试题解析
23. 李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程s（千米）与行驶时间t（小时）的关系如图所示（中途休息、加油的时间不计．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升/千米，请根据图象解答下列问题：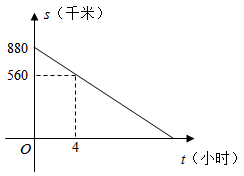

(1)、直接写出工厂离目的地的路程；

(2)、求s关于t的函数表达式；

(3)、当货车显示加油提醒后，问行驶时间t在怎样的范围内货车应进站加油？

查看试题解析
24. 在学习了平行四边形知识以后，根据你学习平行四边形的经验，对平行四边形的问题进行再次探究．请你完成以下任务．

(1)、在四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，若AB//CD，请你添加下列三个条件中的一个，使得四边形 $A B C D$ 是平行四边形．你添加的条件是（选一个正确选项的序号，填写在横线上）
① $A D = B C$ ；② $∠ B A D = ∠ B C D$ ；③ $A O = O C$ ．

(2)、将（1）中你添加条件后的命题用文字语言表述为：．

(3)、画出（2）中命题的图形，写出命题的已知和求证，并完成证明过程．

查看试题解析
25. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图象由函数 $y = \frac{1}{2} x$ 的图象向下平移1个单位长度得到．

(1)、求这个一次函数的解析式；

(2)、当 $x > - 2$ 时，对于 $x$ 的每一个值，函数 $y = m x (m \neq 0)$ 的值大于一次函数 $y = k x + b$ 的值，直接写出 $m$ 的取值范围．

查看试题解析
26. 我们给出如下定义：平面直角坐标系中的线段 $A B$ 及点P，任取 $A B$ 上一点Q，线段 $P Q$ 长度的最小值称为点P到线段 $A B$ 的距离，记作d．

(1)、如图，已知长度为2个单位长度的线段 $M N$ 在x轴上，点M的坐标为 $(1 ， 0)$ ．求点 $P (1 ， 1)$ 到线段 $M N$ 的距离D；

(2)、已知平面直角坐标系内有一点G，到线段 $O E$ ： $y = x (0 \leq x \leq 3)$ 的距离 $d = \sqrt{2}$ ，且点G的横坐标为1，请你画出图象，并求点G的纵坐标．

(3)、在平面直角坐标系中有一点C，到线段 $O E$ ： $y = x (0 \leq x \leq 3)$ 的距离 $d = \sqrt{2}$ ，请你画出点C的轨迹．（点的轨迹定义：符合某一条件的所有的点组成的图形，叫做符合这个条件的点的轨迹）

查看试题解析
27. 已知：点P是平行四边形 $A B C D$ 对角线AC所在直线上的一个动点（点P不与点A、C重合），分别过点A、C向直线BD作垂线，垂足分别为点E、F，点O为AC的中点．

(1)、当点P与点O重合时如图 $1$ ，易证 $O E = O F$ （需证明）；

(2)、直线 $B P$ 绕点B逆时针方向旋转，当 $∠ O F E = 30 °$ 时，如图2、图3的位置，猜想线段 $C F$ 、 $A E$ 、 $O E$ 之间有怎样的数量关系？请写出你对图2、图3的猜想，并选择一种情况给予证明．

查看试题解析