广东省韶关市新丰县2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-02-20 类型:期中考试
一、单选题
-
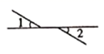
1. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列实数中,是无理数的为( )A、0 B、-1.5 C、π D、3. 若 是方程 的一个解,则 ( )A、 B、2 C、 D、4. 在下图中,∠1和∠2是对顶角的是( )A、
 B、
B、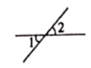 C、
C、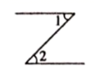 D、
D、 5. 在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )A、 B、 C、 D、6. 16的平方根是( )A、±16 B、±8 C、±4 D、±27. 下列命题中是假命题的是( )A、两点之间,线段最短 B、同旁内角互补 C、等角的补角相等 D、垂线段最短8. 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是( )
5. 在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )A、 B、 C、 D、6. 16的平方根是( )A、±16 B、±8 C、±4 D、±27. 下列命题中是假命题的是( )A、两点之间,线段最短 B、同旁内角互补 C、等角的补角相等 D、垂线段最短8. 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是( ) A、15° B、25° C、35° D、45°9. 下列四幅图中,和是同位角的是( )
A、15° B、25° C、35° D、45°9. 下列四幅图中,和是同位角的是( ) A、①② B、③④ C、①②④ D、②③④10. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏,如图,是一局象棋残局,若表示棋子“炮”和“車”的点的坐标分别为(1,2),(-2,0),则表示棋子“馬”的点的坐标为( )
A、①② B、③④ C、①②④ D、②③④10. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏,如图,是一局象棋残局,若表示棋子“炮”和“車”的点的坐标分别为(1,2),(-2,0),则表示棋子“馬”的点的坐标为( ) A、(-3,3) B、(-3,2) C、(4,2) D、(3,2)11. 如图,某地进行城市规划,在一条新修公路旁有一超市,现要建一个汽车站.为了使超市距离车站最近,请你在公路上选一点来建汽车站,应建在( )
A、(-3,3) B、(-3,2) C、(4,2) D、(3,2)11. 如图,某地进行城市规划,在一条新修公路旁有一超市,现要建一个汽车站.为了使超市距离车站最近,请你在公路上选一点来建汽车站,应建在( ) A、点A B、点B C、点C D、点D12. 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到的位置, , , , 平移距离为4,求阴影部分的面积为( )
A、点A B、点B C、点C D、点D12. 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到的位置, , , , 平移距离为4,求阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 在电影票上如果将“8排4号”记作(8,4),那么“3排5号”记作 .14. 比较大小:5.(填“>”或“<”或“=”)15. 最接近的整数是 .16. 若+(b-2)2=0,则a+b= .17. 若某个正数的两个平方根分别是2a+1与2a-5,则a= .18. 如图,将长方形沿折叠,点D落在边上的H点处,点C落在点G处,若 , 则等于 .

三、解答题
-
19. 计算:( )2一 + .20. 解方程:21. 已知,如图直线AB与CD相交于点O,∠BOE=90°,∠AOD=30°,OF为∠BOD的角平分线.
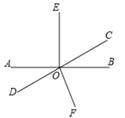 (1)、求∠EOC度数;(2)、求∠EOF的度数.22. 如图所示,已知:∠1=∠2,∠A=35°,∠C=∠D
(1)、求∠EOC度数;(2)、求∠EOF的度数.22. 如图所示,已知:∠1=∠2,∠A=35°,∠C=∠D (1)、 证明:BD//CE ;(2)、 求∠F的度数.23. 如图,平面直角坐标系中,已知点 , , , 是的边上任意一点,经过平移后得到△ , 点P的对应点为 .
(1)、 证明:BD//CE ;(2)、 求∠F的度数.23. 如图,平面直角坐标系中,已知点 , , , 是的边上任意一点,经过平移后得到△ , 点P的对应点为 . (1)、直接写出点 , , 的坐标.(2)、在图中画出△ .(3)、连接 , , , 求的面积.(4)、连接 , 若点Q在y轴上,且三角形的面积为8,请直接写出点Q的坐标.24. 探究:如图①,AB∥CD∥EF,点G、P、H分别在直线AB、CD、EF上,连接PG、PH,当点P在直线GH的左侧时,试说明∠AGP+∠EHP=∠GPH.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式).
(1)、直接写出点 , , 的坐标.(2)、在图中画出△ .(3)、连接 , , , 求的面积.(4)、连接 , 若点Q在y轴上,且三角形的面积为8,请直接写出点Q的坐标.24. 探究:如图①,AB∥CD∥EF,点G、P、H分别在直线AB、CD、EF上,连接PG、PH,当点P在直线GH的左侧时,试说明∠AGP+∠EHP=∠GPH.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式). (1)、填空:如图①,
(1)、填空:如图①,∵AB∥CD(),
∴∠AGP=∠GPD.
∵CD∥EF,
∴∠DPH=∠EHP(),
∵∠GD+∠DPH=∠GPH,
∴∠AGP+∠EHP=∠GPH().
(2)、拓展:将图①的点P移动到直线GH的右侧,其他条件不变,如图②.试探究∠AGP,∠EHP、∠GPH之间的关系,并说明理由.(3)、应用:如图③,AB∥CD∥EF,点G、H分别在直线AB、EF上,点Q是直线CD上的一个动点,且不在直线GH上,连接QG、QH.若∠GQH=70°,请求出∠AGQ+∠EHQ的度数.