广东省茂名市电白区2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-02-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{6} \div a^{2} = a^{4}$ C、 ${(2 a b)}^{3} = 6 a^{3} b^{3}$ D、 $a^{2} \cdot a^{3} = a^{6}$

查看试题解析
2. 2020年1月12日，“2019新型冠状病毒”被世界卫生组织正式命名为“2019—nCoV”，其直径约为0.000000125米．则数据0.000000125用科学记数法表示正确的是（）

A、 $1.25 \times 1 0^{7}$ B、 $1.25 \times 1 0^{- 7}$ C、 $1.25 \times 1 0^{8}$ D、 $1.25 \times 1 0^{- 8}$

查看试题解析
3. 下列图中，∠1与∠2是同位角的是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式中能用平方差公式运算的是（）

A、 $(- a + b) (- a - b)$ B、 $(a - b) (b - a)$ C、 $(2 a - 3 b) (3 a + 2 b)$ D、 $(a - b + c) (b - a - c)$

查看试题解析
5. 已知∠1与∠2互为补角， $∠ 1 = 140 °$ ，则∠2的度数为（）

A、30° B、40° C、50° D、100°

查看试题解析
6. 如果 $m - n = 3$ ， $m n = 1$ ，那么 $m^{2} + n^{2}$ 的值是（）

A、5 B、7 C、9 D、11

查看试题解析
7. 如图，现要从村庄 $A$ 修建一条连接公路 $C D$ 的最短小路，过点 $A$ 作 $A B ⊥ C D$ 于点 $B$ ，沿修建公路，则这样做的理由是（）

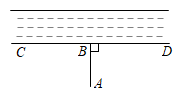A、垂线段最短 B、两点之间，线段最短 C、过一点可以作无数条直线 D、两点确定一条直线

查看试题解析
8.
如图，在四边形 $A B C D$ 中，要得到 $A B ∥ C D$ ，只需要添加一个条件，这个条件可以是（）

A、 $∠ 1 = ∠ 3$ B、 $∠ 2 = ∠ 4$ C、 $∠ B = ∠ D$ D、 $∠ 1 + ∠ 2 + ∠ B = 180 °$

查看试题解析
9. 已知x+y﹣3＝0，则2^x×2^y的值为（）

A、64 B、8 C、6 D、12

查看试题解析
10. 如图，直线EF分别与直线AB，CD相交于点G，H，已知∠1=∠2=50°，GM平分∠HGB交直线CD于点M，则∠3等于（）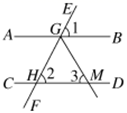

A、60° B、65° C、70° D、130°

查看试题解析

二、填空题

11. ${(2 x + 3)}^{2} =$ ．

查看试题解析
12. 若x²＋2mx＋9是一个完全平方式，则m的值是

查看试题解析
13. 如果一个角的余角等于它本身，那么这个角的补角等于度.

查看试题解析
14. 小明在计算一道整式乘法的题： $(x - m) (3 x + 5)$ ，因为把“-m”抄成了“+m”，得到的结果是 $3 x^{2} + 11 x + 10$ ，则m的值为．

查看试题解析
15. 小华用500元去购买单价为3元的一种商品，剩余的钱数y(元)与购买这种商品的件数x(件)之间的关系是．

查看试题解析
16. 调皮的弟弟把玲玲的作业本撕掉了一角，留下一道残缺不全的题目，如图所示，请你帮她推测出被除式等于．

查看试题解析
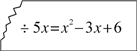17. 如图是由四个相同的长方形拼成的一个大正方形EFCH和一个小正方形ABCD，设小正方形ABCD的面积为 $S_{1}$ ，大正方形EFGH的面积为 $S_{2}$ ，每个长方形的面积为 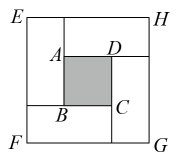$S_{3}$ ．若 $S_{1} = \frac{3}{4} S_{3}$ ，且 $S_{1} + S_{2} = 22$ ，则 $S_{1} =$ ．

查看试题解析

三、解答题

18. 计算：

(1)、 $5 x (2 x^{2} - 3 x + 4)$

(2)、 $(- \frac{1}{5} a^{3} x^{4} + \frac{9}{10} a^{2} x^{3}) \div (- \frac{3}{5} a x^{2})$

查看试题解析
19. 计算：

(1)、 $(3.14 - π)^{0} + | - 2 | - {(\frac{1}{2})}^{- 1}$ ；

(2)、 $202 0^{2} - 2019 \times 2021$ ．（要求用公式简便计算）

查看试题解析
20. 先化简，再求值：
[（x+3y）（x-3y）-（x-3y）²]÷（6y），其中x＝6，y $= - \frac{1}{3}$ ．

查看试题解析
21. 请补全下列推理过程及括号内的推理依据．
已知：如图， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D$ ，请说明 $∠ A = ∠ F$ ．
解：因为 $∠ 1 = ∠ 2$ （已知），
$∠ 1 = ∠ 3$ （      ）．
所以 $∠ 2 = ∠ 3$ （等量代换）．
所以 $B D ∥ C E$ （        ）．
所以 $∠ D = ∠ 4$ （        ）．
又因为 $∠ C = ∠ D$ （已知）．
所以 $∠ C = ∠$       ▲ （等量代换），
所以      ▲ $∥$       ▲ （       ）．
所以 $∠ A = ∠ F$ （       ）．

查看试题解析
22. 如图，直线AB、CD相交于点O，OE把∠BOD分成两部分．

(1)、图中∠AOC的对顶角为， ∠BOE的补角为；

(2)、若∠AOC=75°，且∠BOE∶∠EOD=1∶4，求∠AOE的度数．

查看试题解析
23. 小明家距离学校8千米，今天早晨小明骑车上学途中，自行车突然“爆胎”，恰好路边有便民服务点，几分钟后车修好了，他加快速度骑车到校．我们根据小明的这段经历画了一幅图象，该图描绘了小明行驶路程s与所用时间t之间的函数关系，请根据图象
回答下列问题：

(1)、小明骑车行驶了千米时，自行车“爆胎”；修车用了分钟．

(2)、修车后小明骑车的速度为每小时千米．

(3)、小明离家分钟距家6千米．

(4)、如果自行车未“爆胎”，小明一直按修车前速度行驶，那么他比实际情况早到或晚到多少分钟．

查看试题解析
24. 已知：如图， $A B ∥ E F$ ， $A C ∥ D E$ ．试说明：

(1)、 $∠ B = ∠ F$ ；

(2)、 $∠ 1 = ∠ 2$ ；

(3)、 $∠ A = ∠ E$ ．

查看试题解析
25. 已知 $(a - b) (a + b) = a^{2} - b^{2}$ ．

(1)、 $(2 - 1) (2 + 1) (2^{2} + 1) =$ ；

(2)、求 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) (2^{16} + 1)$ 的值；

(3)、求 $2 (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1) (3^{32} + 1)$ 结果的个位数字．

查看试题解析