广东省惠州市仲恺高新区2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-02-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt[3]{- 8} = 2$ C、 ${(\sqrt{5})}^{2} = \sqrt{5}$ D、 $\sqrt{2^{2}} = 2$

查看试题解析
2. 点 $M (- 2 ， 5)$ 是由点N向上平移3个单位得到的，则点N的坐标为（）

A、 $(2 ， 0)$ B、 $(2 ， 1)$ C、 $(- 2 ， 2)$ D、 $(2 ， - 3)$

查看试题解析
3. 估计 $\sqrt{29}$ 的值在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
4. 下列运动属于平移的是（）

A、冷水加热过程中小气泡上升成为大气泡 B、急刹车时汽车在地面上的滑动 C、投篮时的篮球运动 D、随风飘动的树叶在空中的运动

查看试题解析
5. 下列说法中，正确的是（　　）

A、点P（3，2）到x轴距离是3 B、在平面直角坐标系中，点（2，-3）和点（-2，3）表示同一个点 C、若y＝0，则点M（x，y）在y轴上 D、在平面直角坐标系中，第三象限内点的横坐标与纵坐标同号

查看试题解析
6. 如图，将△ABC沿射线BC方向平移3 cm得到△DEF．若△ABC的周长为14 cm，则四边形ABFD的周长为（）

A、20 cm B、17 cm C、14 cm D、23 cm

查看试题解析
7. 如图，下列条件不能判定 $A B$ ∥ $E F$ 的是（）

A、 $∠ B + ∠ B F E = 180 °$ B、 $∠ B = ∠ 5$ C、 $∠ 3 = ∠ 4$ D、 $∠ 1 = ∠ 2$

查看试题解析
8. 如图， $O A ⊥ O C$ ， $O B ⊥ O D$ ，且 $∠ A O D = 150 °$ ，则 $∠ B O C$ 的度数是（）

A、 $60 °$ B、 $30 °$ C、 $50 °$ D、 $40 °$

查看试题解析
9. 已知 $\sqrt{a - 17} + 2 \sqrt{17 - a} = b + 8$ ，则 $\sqrt{a - b}$ 的值是（）．

A、 $\pm 3$ B、3 C、5 D、 $\pm 5$

查看试题解析
10. 如图所示是一个数值转换器，若输入某个正整数值x后，输出的y值为4，则输入的x值可能为（）

A、10 B、6 C、4 D、1

查看试题解析

二、填空题

11. “平行于同一条直线的两条直线平行”是命题（填“真”或“假”）．

查看试题解析
12. 已知 $\sqrt[3]{425} = 7.25$ ， $\sqrt[3]{42.5} = 3.49$ ，则 $\sqrt[3]{42500} =$ ．

查看试题解析
13. 已知： $\frac{1}{2}$ ， $\frac{π}{2}$ ， $\sqrt{2}$ ， $\overset{}{3} . \overset{•}{7}$ ， $\sqrt{4}$ ， $- \frac{22}{7}$ ，3.1415926，-1， $\sqrt{\frac{4}{9}}$ ， $\sqrt[3]{4}$ ，0.2020020002…（相邻两个2之间0的个数逐次加1）其中无理数有个.

查看试题解析
14. 如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是 $(3 ， 0)$ 和 $(- 3 ， 2)$ ，那么“卒”的坐标为．

查看试题解析
15. 如图，直线l₁∥l₂ ， AB⊥l₁于O，BC与l₂相交于点E，若∠1＝25°，则∠2＝度．

查看试题解析
16. 如图，三角形 $A B C$ 中， $∠ A C B = 90 °$ ， $A C = 6$ ， $B C = 8$ ， P为直线 $A B$ 上一动点，连接 $P C$ ，则线段 $P C$ 的最小值是．

查看试题解析
17. 如图，弹性小球从点 $P (0 ， 3)$ 出发，沿所示方向运动，每当小球碰到长方形 $O A B C$ 的边时反弹，反弹时反射角等于入射角，当小球第1次碰到长方形的边时的点为 $P_{1}$ ，第2次碰到长方形的边时的点为 $P_{2}$ ， …，第n次碰到长方形的边时的点为 $P_{n}$ ，则点 $P_{2015}$ 的坐标是．

查看试题解析

三、解答题

18. 计算： $\sqrt{(- 3)^{2}} + \sqrt[3]{- 8}$ -|-4|．

查看试题解析
19. 已知x﹣2的平方根是±2，2x+y+7的立方根是3，求x²+y²的平方根．

查看试题解析
20. 如图，△A₁B₁C₁是△ABC向右平移四个单位长度后得到的，且三个顶点的坐标分别为A₁（1，1），B₁（4，2），C₁（3，4）.

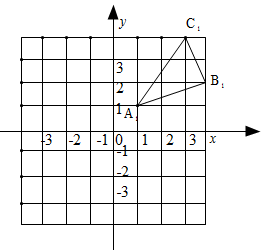(1)、请画出△ABC，并写出点A、B、C的坐标；

(2)、求出△AOA₁的面积.

查看试题解析
21. 已知： $P (4 x ， x - 3)$ 在平面直角坐标系中．

(1)、若点Р在第三象限的角平分线上，求Р点坐标；

(2)、若点Р在第四象限，且到两坐标轴的距离之和为9，求Р点坐标．

查看试题解析
22. 完成下面推理过程：
如图，已知 $∠ 1 = ∠ 2 ， ∠ B = ∠ C$ ，可得 $A B$ // $C D$ ．
理由是：∵ $∠ 1 = ∠ 2$ （已知），
$∠ 1 = ∠ C G D$ （                   ）．
∴ $∠ 2 = ∠ C G D$ （                    ）
∴ $C E$ // $B F$ （                      ）
∴ $∠ B F D = ∠ C$ （                      ）．
∵ $∠ B = ∠ C$ （已知），
∴∠_▲_ $= ∠ B$ （等量代换），
∴ $A B$ // $C D$ （                      ）．

查看试题解析
23.

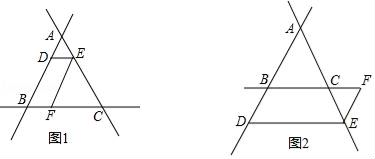(1)、探究：如图1，直线AB、BC、AC两两相交，交点分别为点A、B、C，点D在线段AB上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F．若∠ABC=40°，求∠DEF的度数．

(2)、应用：如图2，直线AB、BC、AC两两相交，交点分别为点A、B、C，点D在线段AB的延长线上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F．若∠ABC=60°，求∠DEF的度数．

查看试题解析
24. 材料1：因为无理数是无限不循环小数，所以无理数的小数部分我们不可能全部写出来．比如： $π$ ， $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确．
材料2：2.5的整数部分是2，小数部分是0.5，小数部分可以看成是2.5-2得来的；
材料3：任何一个无理数，都夹在两个相邻的整数之间，如 $2 < \sqrt{5} < 3$ ，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ．
根据上述材料，回答下列问题：

(1)、 $\sqrt{23}$ 的整数部分是．小数部分是．

(2)、 $9 + \sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为 $a < 9 + \sqrt{3} < b$ ，求 $a + b$ 的值．

(3)、若 $\sqrt{30} - 2 = x + y$ ，其中x是整数，且 $0 < y < 1$ ，请求出 $2 x - y$ 的相反数．

查看试题解析
25. 已知△ABC的三个顶点位置分别是A（1，0），B（-3，0），C（x，y）．

(1)、若x＝-3，y＝3，求△ABC的面积；

(2)、如图，若顶点C（x，y）位于第二象限，且CB∥y轴，AC与y轴相交于点E（0，1），当△ABC沿x轴正半轴方向平移，得到△DOF，且△DOF与原△ABC重叠部分为△AOE，求阴影部分的面积S（用含y的式子表示）；

(3)、若点C到y轴的距离为4，点P（0，5），当S_△ABC＝2S_△ABP，求点C的坐标．

查看试题解析