广东省惠州市2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-02-20 类型:期中考试
一、单选题
-
1. 现实世界中,平移现象无处不在,中国的方块字中有些也具有平移性,下列汉字是由平移构成的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列四个实数中,无理数是( )A、-1 B、 C、0.1010010001 D、3. 如图, , , 能够表示点C到直线的距离的是( ).
2. 下列四个实数中,无理数是( )A、-1 B、 C、0.1010010001 D、3. 如图, , , 能够表示点C到直线的距离的是( ).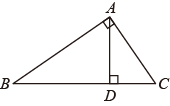 A、的长 B、的长 C、的长 D、的长4. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列各式正确的是( ).A、 B、 C、 D、6. 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A、的长 B、的长 C、的长 D、的长4. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列各式正确的是( ).A、 B、 C、 D、6. 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )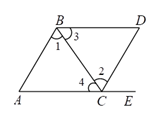 A、∠3=∠4 B、∠1=∠2 C、∠D=∠DCE D、∠D+∠DCA=180°7. 已知点P(2m+4,m﹣1),点Q(2,5),直线PQ y轴,点P的坐标是( )A、(2,2) B、(16,5) C、(﹣2,5) D、(2,﹣2)8. 如图,将一张矩形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的值是( )
A、∠3=∠4 B、∠1=∠2 C、∠D=∠DCE D、∠D+∠DCA=180°7. 已知点P(2m+4,m﹣1),点Q(2,5),直线PQ y轴,点P的坐标是( )A、(2,2) B、(16,5) C、(﹣2,5) D、(2,﹣2)8. 如图,将一张矩形纸片和一张直角三角形纸片叠放在一起,∠1+∠2的值是( ) A、180° B、240° C、270° D、300°9. 下列命题是真命题的有( )个
A、180° B、240° C、270° D、300°9. 下列命题是真命题的有( )个①两条直线被第三条直线所截,同位角相等
②垂直于同一条直线的两条直线互相平行
③过一点有且只有一条直线与已知直线平行
④对顶角相等,邻补角互补
A、1 B、2 C、3 D、410. 如图,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数字之和,例如第4行的6为第3行中两个3的和.若在“杨辉三角”中从第2行左边的1开始按“锯齿形”排列的箭头所指的数依次构成一个数列:a1=1,a2=2.a3=3,a4=3,a5=6,a6=4,a7=10,a8=5…,则a99+a100的值为( ) A、1326 B、1327 C、1328 D、1329
A、1326 B、1327 C、1328 D、1329二、填空题
-
11. = , 36的平方根是 .12. 如图,在立定跳远中,体育老师是这样测运动员的成绩的,用一块三角尺的一边紧贴在起跳线上,另一边与拉直的皮尺重合,这样做的理由是 .
 13. 比较大小: .14. 如图,将一张长方形纸片沿EF折叠后,点A,B分别落在A′,B′的位置.如果∠1=59°,那么∠2的度数是 .
13. 比较大小: .14. 如图,将一张长方形纸片沿EF折叠后,点A,B分别落在A′,B′的位置.如果∠1=59°,那么∠2的度数是 . 15. 李华同学学习二次根式后发现,若 , 则有 . 若 , 则 .16. 已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是.17. 如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN,MF交于点O.若∠E+60°=2∠F,则∠AMF的大小是 .
15. 李华同学学习二次根式后发现,若 , 则有 . 若 , 则 .16. 已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是.17. 如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN,MF交于点O.若∠E+60°=2∠F,则∠AMF的大小是 .
三、解答题
-
18. 计算: .19. 解方程 .20. 完成下列证明过程,并在括号内填上依据.
如图,点E在AB上,点F在CD上,∠1=∠2,ABCD,求证∠B=∠C.

证明:∵∠1=∠2(已知)
∠1=∠4(① )
∴∠2=∠4
∴CEBF(② )
∴∠3=③_▲_(④ )
又∵ABCD(已知)
∴∠3=⑤_▲_(⑥ )
∴∠B=∠C.
21. 正数x的两个平方根分别为3﹣a和2a+7.(1)、求a的值;(2)、求44﹣x这个数的立方根.22. 已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1 . 它们在平面直角坐标系中的坐标如表所示:△ABC
A(a,0)
B(3,0)
C(5,5)
△A1B1C1
A1(-3,2)
B1(-1,b)
C1(c,7)
 (1)、观察表中各对应点坐标的变化,并填空:a= , b= , c=;(2)、在如图的平面直角坐标系中画出△ABC;(3)、求△A1B1C1的面积.23. 如图1,直线EF与AB、CD交于点G、H,∠1=∠3.
(1)、观察表中各对应点坐标的变化,并填空:a= , b= , c=;(2)、在如图的平面直角坐标系中画出△ABC;(3)、求△A1B1C1的面积.23. 如图1,直线EF与AB、CD交于点G、H,∠1=∠3. (1)、求证:AB∥CD;(2)、如图2,若GM⊥GE,∠BGM=20°,HN平分∠CHE,求∠NHD的度数.24. 阅读下面文字,然后回答问题.
(1)、求证:AB∥CD;(2)、如图2,若GM⊥GE,∠BGM=20°,HN平分∠CHE,求∠NHD的度数.24. 阅读下面文字,然后回答问题.给出定义:一个实数的整数部分是不大于这个数的最大数,这个实数的小数部分为这个数与它的整数部分的差的绝对值.例如:2.4的整数部分为2,小数部分为;的整数部分为1,小数部分可用表示;再如,-2.6的整数部分为-3,小数部分为 . 由此我们得到一个真命题:如果 , 其中x是整数,且 , 那么 , .
(1)、如果 , 其中a是整数,且 , 那么a= , b=;(2)、如果 , 其中c是整数,且 , 那么c= , d=;(3)、已知 , 其中m是整数,且 , 求的值;(4)、在上述条件下,求的立方根.25. 在平面直角坐标系中,点 , , ,且 .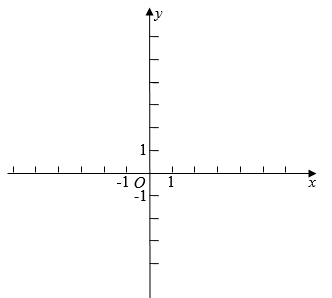 (1)、点 的坐标为 , 点 的坐标为;(2)、将线段 平移至 ,点 和点 为对应点,点 和点 为对应点,当点 和点 分别落在两条坐标轴上时,求点 的坐标;(3)、若点 在第一象限,且在直线 上,点 关于 轴的对称点为点 .若 的面积为8,求点 的坐标.
(1)、点 的坐标为 , 点 的坐标为;(2)、将线段 平移至 ,点 和点 为对应点,点 和点 为对应点,当点 和点 分别落在两条坐标轴上时,求点 的坐标;(3)、若点 在第一象限,且在直线 上,点 关于 轴的对称点为点 .若 的面积为8,求点 的坐标.