广东省广州市白云区六校2021-2022学年下学期七年级期中数学试卷
试卷更新日期:2023-02-20 类型:期中考试
一、单选题
-
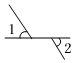
1. 如图,∠1与∠2是对顶角的是( )A、
 B、
B、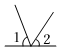 C、
C、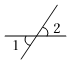 D、
D、 2. 下面正确的是( )A、=±4 B、 C、=2 D、=63. 在3.142、、-、、π、、中,无理数的个数是( )A、2个 B、3个 C、4个 D、5个4. 如图,点在延长线上,下列条件中不能判定的是( )
2. 下面正确的是( )A、=±4 B、 C、=2 D、=63. 在3.142、、-、、π、、中,无理数的个数是( )A、2个 B、3个 C、4个 D、5个4. 如图,点在延长线上,下列条件中不能判定的是( )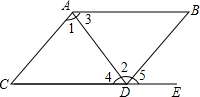 A、 B、 C、 D、5. 下列是二元一次方程组的解的是( )A、 B、 C、 D、6. 如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(-1,-2),“象”位于(1,-2),则“炮”位于点( )
A、 B、 C、 D、5. 下列是二元一次方程组的解的是( )A、 B、 C、 D、6. 如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(-1,-2),“象”位于(1,-2),则“炮”位于点( )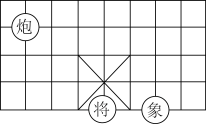 A、(-4,1 ) B、(-3,2) C、(-2,1) D、(-1,-2 )7. 对点(2,-1)叙述错误的是( )A、在x轴下方 B、是由点(2,2)向下平移3个单位所得 C、在第四象限 D、距离y轴1个单位长度8. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是( )A、 B、 C、 D、9. 如图,△ABC中,∠ABC=90°,沿BC所在的直线向右平移得到△DEF,下列结论中,错误的( )
A、(-4,1 ) B、(-3,2) C、(-2,1) D、(-1,-2 )7. 对点(2,-1)叙述错误的是( )A、在x轴下方 B、是由点(2,2)向下平移3个单位所得 C、在第四象限 D、距离y轴1个单位长度8. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x人,女生有y人,根据题意,列方程组正确的是( )A、 B、 C、 D、9. 如图,△ABC中,∠ABC=90°,沿BC所在的直线向右平移得到△DEF,下列结论中,错误的( )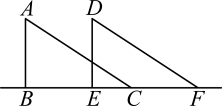 A、EC=CF B、∠A=∠D C、ACDF D、∠DEF=90°10. 小亮解方程组 , 的解为 , 由于不小心滴上了两滴墨水,刚好遮住了两个数▲和☆,则这两个数分别为( )A、4和 - 6 B、- 6和4 C、- 2和8 D、8和 – 2
A、EC=CF B、∠A=∠D C、ACDF D、∠DEF=90°10. 小亮解方程组 , 的解为 , 由于不小心滴上了两滴墨水,刚好遮住了两个数▲和☆,则这两个数分别为( )A、4和 - 6 B、- 6和4 C、- 2和8 D、8和 – 2二、填空题
-
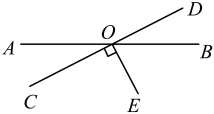
11. 已知方程2x-y=7,若用含x的代数式表示y,则y= .12. 比较大小:π3.14,-- , 2 .13. 如图,已知AB、CD相交于O,OE⊥CD于O,∠AOC=40°,则∠BOE的度数是 °.
 14. 如果点P(x-4,y+1)是坐标原点,则2x+y= .15. 如图:△DEF是△ABC经过某种变换后得到的图形,分别写出A与点D,点B与点E,点C与点F的坐标,并观察它们的关系,如果三角形ABC中任一点M的坐标(x,y),那么它的对应点N的坐标是 .
14. 如果点P(x-4,y+1)是坐标原点,则2x+y= .15. 如图:△DEF是△ABC经过某种变换后得到的图形,分别写出A与点D,点B与点E,点C与点F的坐标,并观察它们的关系,如果三角形ABC中任一点M的坐标(x,y),那么它的对应点N的坐标是 .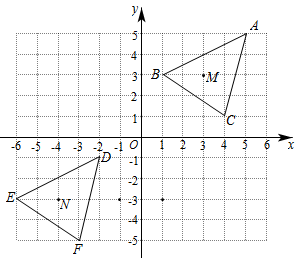 16. 如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到的位置, , , 平移距离为6,则阴影部分的面积为 .
16. 如图,两个直角三角形重叠在一起,将其中一个沿点B到点C的方向平移到的位置, , , 平移距离为6,则阴影部分的面积为 .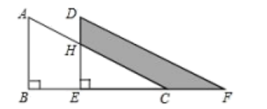
三、解答题
-
17. 计算.(1)、;(2)、 .18. 解下列方程.(1)、;(2)、 .19. 如图,点A表示小明家,点B表示小明外婆家,若小明先去外婆家拿渔具,然后再去河边钓鱼,怎样走路最短,请画出行走路径,并说明理由.
 20. 如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠BOC,∠2:∠1=4:1.
20. 如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠BOC,∠2:∠1=4:1.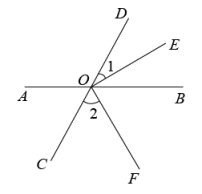 (1)、求∠AOF的度数.(2)、判断OE与OF的位置关系并说明理由.21. 目前某市小学生和初中生共有约128万人,其中小学生人数比初中生人数的2倍多14万人.(1)、求目前某市在校的小学生人数和初中生人数;(2)、假设今年小学生每人需交杂费500元,初中生每人需交杂费1000元,而这些费用全部由市政府拨款解决,则市政府要为此拨款多少?22. 如图,AD//BC,∠1=∠C,∠B=60°.
(1)、求∠AOF的度数.(2)、判断OE与OF的位置关系并说明理由.21. 目前某市小学生和初中生共有约128万人,其中小学生人数比初中生人数的2倍多14万人.(1)、求目前某市在校的小学生人数和初中生人数;(2)、假设今年小学生每人需交杂费500元,初中生每人需交杂费1000元,而这些费用全部由市政府拨款解决,则市政府要为此拨款多少?22. 如图,AD//BC,∠1=∠C,∠B=60°.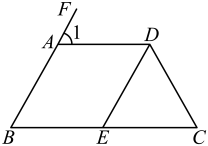 (1)、求∠C=;(2)、若DE是∠ADC的平分线,试判断DE与AB的位置关系,并说明理由.23.
(1)、求∠C=;(2)、若DE是∠ADC的平分线,试判断DE与AB的位置关系,并说明理由.23.如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1 , 点P的对应点为P1(a+6,b﹣2 ).
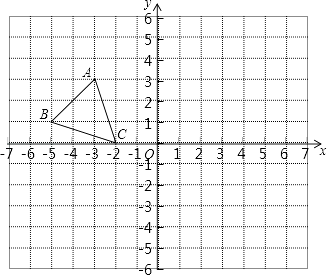 (1)、直接写出点A1 , B1 , C1的坐标.(2)、在图中画出△A1B1C1 .(3)、连接A A1 , 求△AOA1的面积.24. 如图1,在平面直角坐标系中,点A(a,0),B(0,b),且a、b满足.
(1)、直接写出点A1 , B1 , C1的坐标.(2)、在图中画出△A1B1C1 .(3)、连接A A1 , 求△AOA1的面积.24. 如图1,在平面直角坐标系中,点A(a,0),B(0,b),且a、b满足.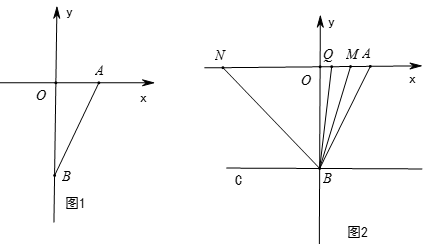 (1)、请直接写出A、B两点的坐标:点A为 , 点B为.(2)、若点P的坐标为(-2,n),且三角形PAB的面积为7,求n的值.(3)、如图2,过点B作BC//x轴,点Q为x轴上点A左侧的一动点,连结QB,BM平分∠QBA,BN平分∠CBA,当点Q运动时,∠MBN:∠AQB的值是否发生变化?如果 变化,请说明理由;如果不变,请求出其值.25. 在平面直角坐标系中,已知点 , , 连接AB,将AB向下平移5个单位得线段CD,其中点A的对应点为点C.
(1)、请直接写出A、B两点的坐标:点A为 , 点B为.(2)、若点P的坐标为(-2,n),且三角形PAB的面积为7,求n的值.(3)、如图2,过点B作BC//x轴,点Q为x轴上点A左侧的一动点,连结QB,BM平分∠QBA,BN平分∠CBA,当点Q运动时,∠MBN:∠AQB的值是否发生变化?如果 变化,请说明理由;如果不变,请求出其值.25. 在平面直角坐标系中,已知点 , , 连接AB,将AB向下平移5个单位得线段CD,其中点A的对应点为点C.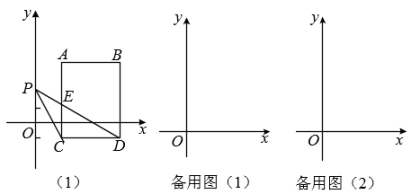 (1)、填空:点C的坐标为 , 线段AB平移到CD扫过的面积为;(2)、若点P是y轴上的动点,连接PD.
(1)、填空:点C的坐标为 , 线段AB平移到CD扫过的面积为;(2)、若点P是y轴上的动点,连接PD.①如图(1),当点P在y轴正半轴时,线段PD与线段AC相交于点E,用等式表示三角形PEC的面积与三角形ECD的面积之间的关系,并说明理由;
②当PD将四边形ACDB的面积分成2:3两部分时,求点P的坐标.