人教版七年级下数学疑难点专题专练——5.2平行线及其证明
试卷更新日期:2023-02-20 类型:同步测试
一、单选题
-
1. 如图,下列条件中,不能判断直线的是( )
 A、∠1=∠2 B、∠3=∠4 C、∠4=∠6 D、∠2+∠5=180°2. 如图,下列推论正确的是( )
A、∠1=∠2 B、∠3=∠4 C、∠4=∠6 D、∠2+∠5=180°2. 如图,下列推论正确的是( ) A、 , B、 , C、 , D、 ,3. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( )
A、 , B、 , C、 , D、 ,3. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( ) A、2个 B、3个 C、4个 D、5个4. 如图,木条a、b、c用螺丝固定在木板上且 , 将木条a、木条b、木条c看作是在同一平面内的三条直线、、 , 若使直线、直线达到平行的位置关系,则下列描述正确的是( )
A、2个 B、3个 C、4个 D、5个4. 如图,木条a、b、c用螺丝固定在木板上且 , 将木条a、木条b、木条c看作是在同一平面内的三条直线、、 , 若使直线、直线达到平行的位置关系,则下列描述正确的是( ) A、木条a、c固定不动,木条b绕点E顺时针旋转 B、木条a、c固定不动,木条b绕点E逆时针旋转 C、木条b、c固定不动,木条a绕点B逆时针旋转 D、木条b、c固定不动,木条a绕点B顺时针旋转5. 如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A、木条a、c固定不动,木条b绕点E顺时针旋转 B、木条a、c固定不动,木条b绕点E逆时针旋转 C、木条b、c固定不动,木条a绕点B逆时针旋转 D、木条b、c固定不动,木条a绕点B顺时针旋转5. 如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( ) A、如图1,展开后测得∠1=∠2 B、如图2,展开后测得∠1=∠2且∠3=∠4 C、如图3,测得∠1=∠2 D、在图4中,展开后测得∠1+∠2=180°6. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )
A、如图1,展开后测得∠1=∠2 B、如图2,展开后测得∠1=∠2且∠3=∠4 C、如图3,测得∠1=∠2 D、在图4中,展开后测得∠1+∠2=180°6. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )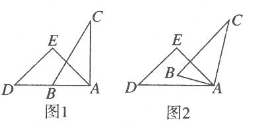 A、 和 B、 和 C、 和 D、以上都有可能7. 为了检验一条纸带的两条边线是否平行,小明沿折叠后,如图,测量得到:①;②;③;④ . 其中能够判定两条边线、互相平行的个数是( )
A、 和 B、 和 C、 和 D、以上都有可能7. 为了检验一条纸带的两条边线是否平行,小明沿折叠后,如图,测量得到:①;②;③;④ . 其中能够判定两条边线、互相平行的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
8. 为增强学生体质,某学校将“抖空竹”引入阳光体育一小时活动.图1是一位同学抖空竹时的一个瞬间,数学老师把它抽象成图2的数学问题:已知AB∥CD,∠EAB=80°,∠ECD=110°.求∠AEC的度数.小明在解决过程中,过E点作EF∥CD,则可以得到EF∥AB,其理由是 , 根据这个思路可得∠AEC=°.

三、解答题
-
9. 如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.
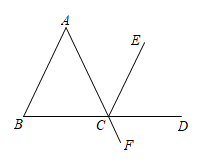
 10. 如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: .
10. 如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: .请完成下列推理过程:
证明:∵CD 平分∠ECF
∴∠ECD= ▲ ( )
∵∠ACB=∠FCD( )
∴∠ECD=∠ACB( )
∵∠B=∠ACB
∴∠B=∠▲( )
∴ ( ).
11. 完成下面的证明:如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.
完成推理过程:
BE平分∠ABD(已知),
∴∠ABD=2∠α( ).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β( )
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( )
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°( ).
∴AB∥CD( ).
12. 完成下面推理填空:如图,E,F分别在AB和CD上, , 与互余,于G.
求证: .

证明:∵ , ∴( ),
∵(已知),∴ ▲ ▲ ( ),
∴( ),
∵(平角的定义),∴ .
∵与互余(已知),∴(互余的定义),
∴( ),∴( ).
13. 把下面的说理过程补充完整:已知,如图,直线AB,CD被直线EF所截,点H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.试说明: .
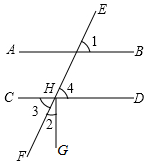
解:∵GH⊥CD( ),
∴∠CHG=90°( ).
又∵∠2=30°( ),
∴∠3=( ).
∴∠4=60°( ).
又∵∠1=60°( ),
∴∠1=∠4( ).
∴( ).
14. 如图, , , .问吗?为什么? 15. 已知:如图.在△ABC中.点D,E,F分到在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°.∠DEF=∠B,求证:DE∥BC.
15. 已知:如图.在△ABC中.点D,E,F分到在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°.∠DEF=∠B,求证:DE∥BC.
四、综合题
-
16. 三角板是学习数学的重要工具 ,将一副三角板的直角顶点 C 按如图所示的方式叠放在一起, 当 时 ,且点 E 在直线AC 的上方时, 解决下列问题∶ (友情提示 ∶ ∠A=60°,∠D=30°,∠B=∠E=45°)
 (1)、①若 ∠DCE=45°,求∠ACB;
(1)、①若 ∠DCE=45°,求∠ACB;②若∠ACB=140°,求∠DCE ;
(2)、由(1)猜想 ∠ACB与∠DCE的数量关系,并说明理由;(3)、这两块三角板是否存在一组边互相平行?若存在,请直接写出∠ACE的所有可能的值(不必说明理由);若不存在,请说明理由.
17. 如图,在中, , 垂足为D,点E在上, , 垂足为F. (1)、求证:(2)、如果 , 求证: .18. 已知, , ∠B=∠A=100°,试回答下列问题:
(1)、求证:(2)、如果 , 求证: .18. 已知, , ∠B=∠A=100°,试回答下列问题: (1)、如图1所示,试说明:;(2)、如图2,若点E,F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数;(3)、在(2)的条件下,若平行移动AC,如图3,则∠OCB∶∠OFB的值是 .
(1)、如图1所示,试说明:;(2)、如图2,若点E,F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数;(3)、在(2)的条件下,若平行移动AC,如图3,则∠OCB∶∠OFB的值是 .
-


