2023年苏科版数学七年级下册全方位训练卷10.5用二元一次方程解决问题

试卷更新日期：2023-02-19 类型：同步测试

进入出卷网下载

一、单选题（每题2分，共16分）

1. 《九章算术》卷八方程第十题原文为：“今有甲、乙二人持钱不知其数．甲得乙半而钱五十，乙得甲太半而亦钱五十．问：甲、乙持钱各几何？”题目大意是：甲、乙两人各带了若干钱．如果甲得到乙所有钱的一半，那么甲共有钱50；如果乙得到甲所有钱的 $\frac{2}{3}$ ，那么乙也共有钱50．问：甲、乙两人各带了多少钱？设甲、乙两人持钱的数量分别为x，y，则可列方程组为（）

A、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$ B、 ${\begin{array}{l} x - \frac{1}{2} y = 50 \\ y - \frac{2}{3} x = 50 \end{array}$ C、 ${\begin{array}{l} 2 x + y = 50 \\ x + \frac{2}{3} y = 50 \end{array}$ D、 ${\begin{array}{l} 2 x - y = 50 \\ x - \frac{2}{3} y = 50 \end{array}$

查看试题解析
2. 如图，宽为40cm的长方形图案由10个相同的小长方形拼成，其中一个小长方形的面积为（）

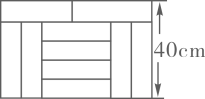A、256cm² B、320cm² C、360cm² D、400cm²

查看试题解析
3. 我校运动员分组训练，若每组7人，余3人；若每组8人，则缺5人，设运动员人数为 $x$ 人，组数为 $y$ 组，则列方程组为（）

A、 ${\begin{array}{l} 7 y = x - 3 \\ 8 y + 5 = x \end{array}$ B、 ${\begin{array}{l} 7 y = x + 3 \\ 8 y + 5 = x \end{array}$ C、 ${\begin{array}{l} 7 y = x - 3 \\ 8 y = x + 5 \end{array}$ D、 ${\begin{array}{l} 7 y = x + 3 \\ 8 y = x + 5 \end{array}$

查看试题解析
4. 顺风旅行社组织200人到花果岭和云水涧旅游，到花果岭的人数比到云水涧的人数的2倍少1人．设到花果岭的人数为x人，到云水涧的人数为y人，根据题意可列方程组为（）

A、 ${\begin{matrix} x + y = 200 \\ x = 2 y - 1 \end{matrix}$ B、 ${\begin{matrix} x + y = 200 \\ y = 2 x - 1 \end{matrix}$ C、 ${\begin{matrix} x + y = 200 \\ x = 2 y + 1 \end{matrix}$ D、 ${\begin{matrix} x + y = 200 \\ y = 2 x + 1 \end{matrix}$

查看试题解析
5. 某种商品价格为33元/件，某人只带有2元和5元的两种面值的购物券各若干张，买了一件这种商品；若无需找零钱，则他的付款方式共有（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
6. 有一个两位数，十位上的数与个位上的数之和为5.这样的两位数（正整数）有（）

A、4个 B、5个 C、6个 D、无数个

查看试题解析
7. 王阿姨和张妈妈通过外卖平台订购了两包蔬菜.王阿姨订购的一包蔬菜包括西葫芦、茄子﹑青椒各1千克，共花费11.8元；张妈妈订购的一包蔬菜包括西葫芦2千克，茄子1.5千克，共花费13元.已知青椒4.2元/千克，则西葫芦和茄子的价格分别是（）

A、3.6元/千克、4元/千克 B、4.4元/千克、3.2元/千克 C、3.2元/千克、4.4元/千克 D、4元/千克、3.6元/千克

查看试题解析
8. 小王沿街匀速行走，发现每隔12分钟从背后驶过一辆8路公交车，每隔4分钟从迎面驶来一辆8路公交车．假设每辆8路公交车行驶速度相同，而且8路公交车总站每隔固定时间发一辆车，那么发车间隔的时间是（）

A、3分钟 B、4分钟 C、5分钟 D、6分钟

查看试题解析

二、填空题（每空2分，共20分）

9. 《九章草术》是人类科学史上应用数学的“算经之首”，书中记载：今有三人共车，二车空；二人共车，九人步．问：人与车各几何？译文：若3人坐一辆车，则两辆车是空的；若2人坐一辆车，则9人需要步行，问：人与车各多少？设有 $x$ 辆车，人数为 $y$ ，根据题意可列方程组为．

查看试题解析

10. 周末小明和妈妈外出共消费了300元，表中记录了他一天所有的消费项目以及部分支出．如果饼干每包13元，矿泉水每瓶2元，那么小明买了包饼干、瓶矿泉水．

项目

早餐

午餐

购买书籍

饼干

矿泉水

支出金额

（单位：元）

100

130

查看试题解析

11. 六年前，甲的年龄是乙的年龄的3倍，现在甲的年龄是乙的年龄的2倍，则甲比乙大岁.

查看试题解析
12. 把长都是宽的两倍的1个大长方形纸片和4个相同的小长方形纸片按图①、图②方式摆放，则图②中的大长方形纸片未被4个小长方形纸片覆盖部分的面积为cm².

查看试题解析
13. 如图，3个平衡的天平左盘中“〇”、“□”分别表示两种质量不同的物体，则第三个天平右盘中砝码的质量为.

查看试题解析
14. 动物园有一群鸵鸟和长颈鹿，它们共有30只眼睛和44只脚，则鸵鸟有只，长颈鹿有只.

查看试题解析
15. 甲、乙二人都以不变的速度在环形跑道上跑步，如果同时同地出发，相向而行，每隔 $3$ 分钟相遇一次；如果同向而行，每隔 $7$ 分钟相遇一次.已知甲比乙跑得快，则甲每分钟跑圈.

查看试题解析
16. 某旅店一共70个房间，大房间每间住8个人，小房间每间住6个人，一共480个学生刚好住满．设大房间有x个，小房间有y个，则列出方程组为．

查看试题解析

三、解答题（共11题，共84分）

17. 商店里把塑料凳整齐地叠放在一起，据图中提供的信息，当有10张塑料凳整齐地叠放在一起时，总高度是多少厘米？

查看试题解析
18. 如图，在 $3 \times 3$ 的方格内，填写了一些代数式和数．在图中各行、各列及斜对角上的三个数之和都相等，请你求出x，y的值及左下角的方格内应填的数．

查看试题解析
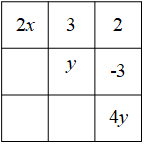19. 阅读理解下面内容，并解决问题：
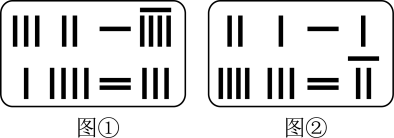
《九章算术》是我国东汉年间编订的一部数学经典著作，在它的“方程”一章里，一次方程组是由算筹布置而成的，《九章算术》中的算筹图是竖排的，为看图方便，把它改为横排，如图①，②，图中各行从左到右列出的算筹数分别表示未知数x，y的系数与对应的常数项，把图①所示的算筹图用方程组形式表述出来，就是 ${\begin{array}{l} 3 x + 2 y = 19 \\ x + 4 y = 23 \end{array}$ ．
类似地，写出图②所示的算筹图的表述形式并求解．

查看试题解析
20. 亚洲文明对话大会召开期间，大批的大学生志愿者参与服务工作．某大学计划组织本校只调配22座新能源客车，则用车数量将增加4辆，并空出2个座位．

(1)、计划调配36座新能源客车多少辆？该大学共有多少名志愿者？

(2)、若同时调配36座和22座两种车型，既保证每人有座，又保证每车不空座，则两种车型各需多少辆？

查看试题解析
21. 阅读感悟：
已知实数x，y满足3x-y=5①，2x+3y=7②，求x-4y和7x+5y的值．
本题常规思路是将①②两式联立组成方程组，解得x，y的值再代人欲求值的式子中得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得式子的值，如由①－②可得x－4y=-2，由①+②×2可得7x+5y= 19．这样的解题思路就利用了通常所说的“整体思想”．

(1)、[解决问题]已知二元一次方程组 ${\begin{array}{l} x + 3 y = 6 \\ 3 x + y = 10 \end{array}$ ，则x-y= ， x+y=

(2)、[拓展延伸]某班级组织活动需购买小奖品，买18支铅笔、27本笔记本共需86.4元，买22支铅笔、13本笔记本共需53.6元，则购买5支铅笔、5本笔记本共需多少元？

查看试题解析
22. 为美化学校环境，建设绿色校园，陶治师生情操我校计划用180元购买A、B两种花卉苗共20棵，已知A种花卉苗每棵12元，B种花卉苗每棵8元.

(1)、根据题意，甲、乙两个同学分别列出了尚不完整的方程组如下：
$甲 : {\begin{cases} x + y = ① \\ 12 x + 8 y = ② \end{cases} 乙： {\begin{cases} x + y = ③ \\ \frac{x}{12} + \frac{y}{8} = ④ \end{cases}$

①；②；③；④。

根据甲、乙两名同学所列的方程组，请你分别指出未知数x,y表示的意义，然后在方框中补全甲、乙两名同学所列的方程组：

甲：x表示， y表示；

乙：x表示， y表示；

(2)、求A、B两种花卉各多少棵？（写出完整的解答过程）

查看试题解析
23. 疫情防控，人人有责，做好新冠肺炎疫情防控时刻不能放松，因此某校举办“疫情防控”宣传活动，计划购买 $A 、 B$ 两种奖品以鼓励积极参与的学生.经市场调查发现，若购买 $A$ 种1件、 $B$ 种2件，共需24元；若购买 $A$ 种3件、 $B$ 种1件，共需52元. $A 、 B$ 两种奖品每件各多少元?

查看试题解析
24. 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种玩具.据了解，8只“冰墩墩”和10只“雪容融”的进价共计2000元；10只“冰墩墩”和20只“雪容融”的进价共计3100元.

(1)、求“冰墩墩”和“雪容融”两种玩具每只进价分别是多少元；

(2)、若“冰墩墩”和“雪容融”两种玩具每只售价分别是200元、100元.该专卖店计划恰好用3500元购进“冰墩墩”和“雪容融”两种玩具（两种均买），请帮助专卖店设计采购方案，使得总利润最大.

查看试题解析
25. 某工厂将一批纸板按甲，乙两种方式进行加工，再用加工出来的长方形 $A$ 板块和正方形 $B$ 板块制作成如图所示的底面为正方形的长方体有盖礼盒. 设x块纸板按甲方式进行加工，y块纸板按乙方式进行加工.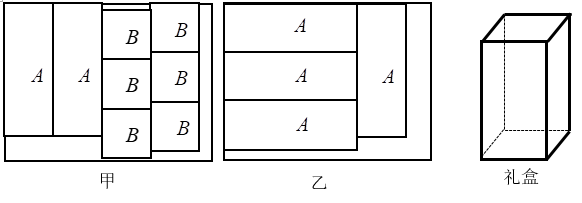

(1)、补全表格.

x块甲方式加工的纸板

y块乙方式加工的纸板

$A$ 板块

2x

$B$ 板块

\

(2)、若现共有纸板14块，要使礼盒制作完毕后的 $A$ ， $B$ 板块恰好用完，能做多少个礼盒？

(3)、若现有 $B$ 板块4块，纸板a块，要使礼盒制作完毕后的 $A$ ， $B$ 板块恰好用完，则a的最小值为. (请直接写出答案)

查看试题解析
26. 已知△ABC的面积是60，请完成下列问题：

(1)、如图1，若AD是△ABC的BC边上的中线，则△ABD的面积 △ACD的面积．（填“＞”“＜”或“＝”）

(2)、如图2，若CD、BE分别是△ABC的AB、AC边上的中线，求四边形ADOE的面积可以用如下方法：连接AO，由AD＝DB得：S_△ADO＝S_△BDO ，同理：S_△CEO＝S_△AEO ，设S_△ADO＝x，S_△CEO＝y，则S_△BDO＝x，S_△AEO＝y由题意得：S_△ABE＝ $\frac{1}{2}$ S_△ABC＝30，S_△ADC＝ $\frac{1}{2}$ S_△ABC＝30，可列方程组为： ${\begin{array}{l} 2 x + y = 30 \\ x + 2 y = 30 \end{array}$ ，解得，通过解这个方程组可得四边形ADOE的面积为．

(3)、如图3，AD：DB＝1：3，CE：AE＝1：2，请你计算四边形ADOE的面积，并说明理由．

查看试题解析
27. 如图1是某机场的平地电梯，电梯AB的长度为120米，如图2所示.若两人不乘电梯在地面匀速行走，小明每分钟的路程是小王的1.5倍，且1.5分钟后，小明比小王多行走30米.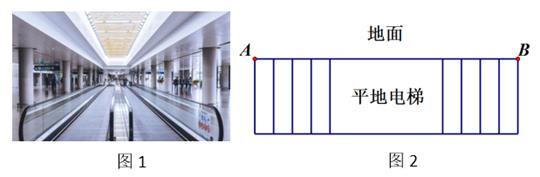

(1)、求两人在地面上每分钟各行走多少米？

(2)、若两人在平地电梯上行走，电梯向前行驶，两人也同时在电梯上行走.当小明到达B处时，小王还剩 $\frac{80}{3}$ 米.
①求平地电梯每分钟行驶多少米？

②当小明到达B处时，发现有一袋行李忘在A处，同时关注此时为7点55分，小明马上从地面返回A处，拿了行李后立即乘平地电梯（同时行走）去B处.问小明能否在8点前和小王汇合，并说明理由.

查看试题解析

	x块甲方式加工的纸板	y块乙方式加工的纸板
$A$ 板块	2x
$B$ 板块		\