2023年苏科版数学七年级下册全方位训练卷10.4三元一次方程组

试卷更新日期：2023-02-19 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共24分）

1. 下列方程组中，是三元一次方程组的是（）

A、 ${\begin{array}{l} x + y = 0 \\ y + z = 1 \\ z + w = 5 \end{array}$ B、 ${\begin{array}{l} x + y = 0 \\ y + 2 x = 1 \end{array}$ C、 ${\begin{array}{l} 3 x + 4 z = 7 \\ 2 x + 3 y = 9 - z \\ 5 x - 9 y + 7 z = 8 \end{array}$ D、 ${\begin{array}{l} x^{2} - 2 y = 0 \\ y + z = 3 \\ x + y + z = 1 \end{array}$

查看试题解析
2. 解三元一次方程组 ${\begin{cases} x - y + z = - 3 ， ① \\ x + 2 y - z = 1 ， ② \\ x + y = 0 ， ③ \end{cases}$ 要使解法较为简便，首先应进行的变形为（）

A、①+② B、①-② C、①+③ D、②-③

查看试题解析
3. 三元一次方程组 ${\begin{array}{l} x + y = 3 \\ y + z = 5 \\ x + z = 4 \end{array}$ ，的解为（）

A、 ${\begin{array}{l} x = 1 \\ y = 3 \\ z = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1 \\ z = 3 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 2 \\ z = 1 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 2 \\ z = 3 \end{array}$

查看试题解析
4. 若： $4 x - 3 y - 6 z = 0$ ， $x + 2 y - 7 z = 0$ ， $(x y z \neq 0)$ ，则：代数式 $\frac{5 x^{2} + 2 y^{2} - z^{2}}{2 x^{2} - 3 y^{2} - 10 z^{2}}$ 的值等于（）

A、 $- \frac{1}{2}$ B、 $- \frac{19}{2}$ C、-15 D、-13

查看试题解析
5. 设“●■▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，如果要使第三架天平也平衡，那么“？”处应放“■”的个数为（）

A、5 B、4 C、3 D、2

查看试题解析
6. 在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元钱购买A、B、C三种奖品，A种每个10元，B种每个20元，C种每个30元，在C种奖品不超过两个且钱全部用完的情况下，购买方案有（）

A、12种 B、14种 C、15种 D、16种

查看试题解析
7. 某宾馆有单人间，双人间，三人间三种客房供游客选择居住，现某旅游团有20名旅客同时安排游客居住在该宾馆，若每个房间都住满，共租了9间客房，则居住方案（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
8. 小明和小亮在一起探究一个数学活动.首先小亮站立在箱子上，小明站立在地面上（如图1），然后交换位置（如图2），测量的数据如图所示，想要探究的问题有：①小明的身高；②小亮的身高；③箱子的高度；④小明与小亮的身高和.根据图上信息，你认为可以计算出的是（）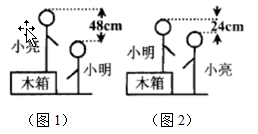

A、① B、② C、③ D、④

查看试题解析

二、填空题（每空3分，共30分）

9. 方程组 ${\begin{array}{l} 3 x - 2 y = 8 \\ 2 y + 3 z = 1 \\ x + 5 z = 7 \end{array}$ 的解是．

查看试题解析
10. 已知三元一次方程组 ${\begin{array}{l} x + y = 3 \\ y + z = 4 \\ x + z = 5 \end{array}$ ，则 $x + y + z =$ .

查看试题解析
11. 解方程组 ${\begin{matrix} x + y + z = 12 \\ x + 2 y - z = 6 \\ 3 x - y + z = 10 \end{matrix}$ 时，消去字母z ，得到含有未知数x ， y的二元一次方程组是．

查看试题解析
12. 若正数a，b，c满足abc=1， $a + \frac{1}{b} = 3 ， b + \frac{1}{c} = 17$ ，则 $c + \frac{1}{a} =$ .

查看试题解析
13. 在等式 y=ax²+bx+c 中，当 x=-1 时， y=0 ；当 x=2 ， y=3 ；当 x=5 时， y=60 ，则a= ， b= ， c= ．

查看试题解析
14. 已知关于x、y的方程 ${\begin{array}{l} 2 x + y = 2 a + 1 \\ x + 2 y = 5 - 5 a \end{array}$ 的解满足 $x + y = - 3$ ，则a的值为.

查看试题解析
15. 有A、B、C三种商品，如果购5件A、2件B、3件C共需513元，购3件A、6件B、5件C共需375件，那么购A、B、C各一件共需元.

查看试题解析
16. 全球棉花看中国，中国棉花看新疆．新疆长绒棉花是世界顶级棉花，品质优，产量大，常年供不应求．綦江区某超市为了支持新疆棉花，在“五一节”进行促销活动，将新疆棉制成 $A$ 、 $B$ 、 $C$ 三种品牌毛巾混装成甲、乙、丙三种礼包销售，其中甲礼包含1条 $A$ 品牌毛巾、2条 $B$ 品牌毛巾；乙礼包含2条 $A$ 品牌毛巾、2条 $B$ 品牌毛巾， 2条 $C$ 品牌毛巾；丙礼包含2条 $A$ 品牌毛巾、2条 $C$ 品牌毛巾，每个礼包的售价等于礼包各条毛巾售价之和，5月1日当天，超市对 $A$ 、 $B$ 、 $C$ 三个品牌毛巾的售价分别打8折、 $7$ 折、 $5$ 折销售，5月2日恢复原价，小明发现5月1日一个甲礼包的售价等于5月2日一个乙礼包售价的 $30 %$ ，5月1日一个乙礼包的售价比5月2日一个丙礼包售价少2.4元，若 $A$ 、 $B$ 、 $C$ 三个品牌的毛巾原价都是正整数，且 $B$ 品牌毛巾的原价不超过14元，则小明在5月1日购买的二个甲礼包和一个乙礼包，应该付元．

查看试题解析

三、计算题（共6分）

17. ${\begin{array}{l} \begin{array}{l} 2 x - 3 y + 4 z = 12 \\ x - y + 3 z = 4 \end{array} \\ 4 x + y - 3 z = - 2 \end{array}$

查看试题解析

四、解答题（共7题，共60分）

18. 甲、乙两人同解方程组 ${\begin{array}{l} A x + B y = 2 \\ C x - 3 y = - 2 \end{array}$ ，甲正确解得 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ ，乙因抄错C解得 ${\begin{array}{l} x = 2 \\ y = - 6 \end{array}$ ，求A、B、C的值．

查看试题解析
19. 现有A,B,C三箱橘子，其中A、B两箱共100个橘子，A、C两箱共102个，B,C两箱共106个，求每箱各有多少个？

查看试题解析
20. 若a，b，c表示三角形的三边，此三角形的周长是18，且a+b=2c，b=2a，求三边长.

查看试题解析
21. 有一个三位数，个位数字是百位数字的3倍，十位数字比百位数字大5，若将此数的个位数与百位数互相对调，所得新数比原数的2倍多35，求原数．

查看试题解析
22. 某校为了做好大课间活动，计划用400元购买10件体育用品，备选体育用品及单价如下表（单位：元）

备选体育用品

篮球

排球

羽毛球拍

单价（元）

50

40

25

(1)、若400元全部用来购买篮球和羽毛球拍共10件，问篮球和羽毛球拍各购买多少件？

(2)、若400元全部用来购买篮球、排球和羽毛球拍三种共10件，能实现吗？（若能实现直接写出一种答案即可，若不能请说明理由.）

查看试题解析
23. 我国古代民间把正月正、二月二、三月三、五月五、六月六、七月七、九月九这“七重”列为吉庆日；“七”在生活中表现为时间的阶段性，比如一周有“七天”……在数的学习过程中，有一类自然数具有的特性也和“七”有关.
定义：对于四位自然数 $n$ ，若其千位数字与个位数字之和等于7，百位数字与十位数字之和也等于7，则称这个四位自然数 $n$ 为“七巧数”.

例如：3254是“七巧数”，因为 $3 + 4 = 7$ ， $2 + 5 = 7$ ，所以3254是“七巧数”； 1456不是“七巧数”，因为 $1 + 6 = 7$ ，但 $4 + 5 \neq 7$ ，所以1456不是“七巧数”.

(1)、若一个“七巧数”的千位数字为 $a$ ，则其个位数字可表示为（用含 $a$ 的代数式表示）；

(2)、最大的“七巧数”是，最小的“七巧数”是；

(3)、若 $m$ 是一个“七巧数”，且 $m$ 的千位数字加上十位数字的和，是百位数字减去个位数字的差的3倍，请求出满足条件的所有“七巧数” $m$ .

查看试题解析
24. 阅读感悟：
有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：

已知实数x、y满足 $3 x - y = 5$ ①， $2 x + 3 y = 7$ ②，求 $x - 4 y$ 和 $7 x + 5 y$ 的值.

本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大.其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由① $-$ ②可得 $x - 4 y = - 2$ ，由① $+$ ② $\times 2$ 可得 $7 x + 5 y = 19$ .这样的解题思想就是通常所说的“整体思想”.

解决问题：

(1)、已知二元一次方程组 ${\begin{array}{l} 2 x + y = 7 \\ x + 2 y = 8 \end{array}$ ，则 $x - y =$ ， $x + y =$ ；

(2)、某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？

(3)、对于实数x、y，定义新运算： $x * y = a x + b y + c$ ，其中a、b、c是常数，等式右边是通常的加法和乘法运算.已知 $3 * 5 = 15$ ， $4 * 7 = 28$ ，那么 $1 * 1 =$ .

查看试题解析

备选体育用品	篮球	排球	羽毛球拍
单价（元）	50	40	25