2023年苏科版数学七年级下册全方位训练卷9.4乘法公式

试卷更新日期：2023-02-19 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共24分）

1. 如图有三种不同的纸片，现选取4张拼成了图甲，你能根据面积关系得到下列等式成立的是（）

A、 $a (a + b) = a^{2} + a b$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

查看试题解析
2. 如图中能够用图中已有图形的面积说明的等式是（）

A、 $x (x + 4) = x^{2} + 4 x$ B、 $(x + 2) (x - 2) = x^{2} - 4$ C、 $(x + 2)^{2} = x^{2} + 4 x + 4$ D、 $(x + 4) (x - 4) = x^{2} - 16$

查看试题解析
3. 已知a-b＝3，ab＝2，则a²-ab+b²的值为（）

A、9 B、13 C、11 D、8

查看试题解析
4. 下列计算中，正确的是（）

A、-a（3a²-1）＝-3a³-a B、（a-b）²＝a²-b² C、（-2a-3）（2a-3）＝9-4a² D、（2a-b）²＝4a²-2ab+b²

查看试题解析
5. 下列多项式，能用平方差公式分解的是（）

A、 $- x^{2} - 4 y^{2}$ B、 $9 x^{2} + 4 y^{2}$ C、 $- x^{2} + 4 y^{2}$ D、 $x^{2} + (- 2 y)^{2}$

查看试题解析
6. 已知 $n$ 为自然数，则 ${(n + 1)}^{2} - {(n - 3)}^{2}$ 一定能被下列哪个数整除？（）

A、5 B、6 C、7 D、8

查看试题解析
7. 若M＝（x - 2）（x - 5），N＝（x - 2）（x - 6），则M与N的关系为（）

A、M＝N B、M＞N C、M＜N D、不能确定

查看试题解析
8. 把一块边长为 $a$ 米（ $a > 5$ ）的正方形土地的一边增加5米，相邻的另一边减少5米，变成一块长方形土地，你觉得土地的面积（）

A、没有变化 B、变大了 C、变小了 D、无法确定

查看试题解析

二、填空题（每题2分，共16分）

9. 已知(m-n)²=40，(m+n)²=4000，则m²+n²的值为.

查看试题解析
10. 已知 $m^{2} - n^{2} = 20$ ， $m + n = 5$ ，则 $m - n =$ ．

查看试题解析
11. 若 ${(x + y)}^{2} = 12$ ， ${(x - y)}^{2} = 8$ ，则xy= ．

查看试题解析
12. $(2 x + 3 y + 5) (2 x + 3 y - 5) =$ ．

查看试题解析
13. 计算： $202 1^{2} - 2020 \times 2022 =$ .

查看试题解析
14. 已知 ${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$ ，则 ${(a - b)}^{4} =$ ．

查看试题解析
15. 如图，两个正方形边长分别为a、b，且满足 $a + b = 6$ ， $a b = 4$ ，图中阴影部分的面积为.

查看试题解析
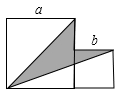16. 用如图所示的正方形和长方形卡片若干张，拼成一个边长为a＋3b的正方形，需要B类卡片张.

查看试题解析

三、计算题（共6题，共40分）

17. 计算

(1)、 $a \cdot a^{4} \cdot {(- a^{2})}^{3}$

(2)、 $3 a (2 a^{2} - 4 a + 3) - 2 a^{2} (3 a - 4)$

(3)、 $(\frac{3}{2} a + 4 b - c) (\frac{3}{2} a - 4 b + c)$

(4)、 ${(x - y)}^{2} - x (3 x - 2 y) + (x + y) (x - y)$

查看试题解析
18. 计算：（a-2b+3c）（a+2b-3c）．

查看试题解析
19. 计算：

(1)、 $(2 a + 3 b) (2 a - 3 b) - {(a - 3 b)}^{2}$ ；

(2)、 $(9 x^{3} y - 12 x y^{3} + 3 x y^{2}) \div (- 3 x y) - (2 y + x) (2 y - x)$ ．

查看试题解析
20. 利用平方差公式计算： $81 \times 79$ ．

查看试题解析
21. 利用乘法公式计算： $2021^{2} + 2020 \times (- 2022)$

查看试题解析
22. 如果 ${(x^{3} - 3 a + \frac{1}{x^{3}})}^{2} + {(x + 2 b + \frac{1}{x})}^{2} = 0$ ，求 $3 a + 2 b (4 b^{2} - 3)$ 的值．

查看试题解析

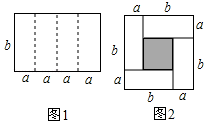
四、解答题（共5题，共40分）

23. 以下是方方化简 $(2 x + y) (2 x - y) + 4 (x + y)^{2}$ 的解答过程．
解： $(2 x + y) (2 x - y) + 4 (x + y)^{2}$
$= 4 x^{2} - y^{2} + 4 (x^{2} + y^{2})$
$= 4 x^{2} - y^{2} + 4 x^{2} + y^{2}$
$= 8 x^{2}$ ．
方方的解答过程是否有错误？如果有错误，写出正确的解答过程．

查看试题解析
24. 已知 $A = {(x - 2 y)}^{2} - (x - y) (x + 2 y)$ ， $B = (2 x^{3} y - 5 x^{2} y^{2} + 2 x^{2} y + 6 x y^{3}) \div x y$ ．

(1)、化简A和B；

(2)、若变量y满足2y＋A＝B－4，求出y与x的关系式；

(3)、在（2）的条件下，求 $x (- 1 + 2 x + x y) - x (x - 1) (x + 1) - {(x - y - 2)}^{2}$ 的值．

查看试题解析
25. 阅读下列文字，并解决问题.
已知 $x^{2} y = 3$ ，求 $2 x y (x^{5} y^{2} - 3 x^{3} y - 4 x)$ 的值.
分析：考虑到满足 $x^{2} y = 3$ 的x，y的可能值较多，不可能逐一代入求解，故考虑整体思想，将 $x^{2} y = 3$ 整体代入.
解： $2 x y (x^{5} y^{2} - 3 x^{3} y - 4 x)$
$= 2 x^{6} y^{3} - 6 x^{4} y^{2} - 8 x^{2} y$
$= 2 (x^{2} y)^{3} - 6 (x^{2} y)^{2} - 8 x^{2} y$
$= 2 \times 3^{3} - 6 \times 3^{2} - 8 \times 3$
$= - 24$ .
请你用上述方法解决问题：

(1)、已知 $a b = 2$ ，求 $(2 a^{3} b^{2} - 3 a^{2} b + 4 a) \cdot (- 2 b)$ 的值；

(2)、已知 $x - \frac{1}{x} = 3$ ，求 $x^{2} + \frac{1}{x^{2}}$ 的值.

查看试题解析
26. 如图，在边长为a的正方形上裁去边长为b的正方形.

(1)、图1，阴影面积是；

(2)、图2是将图1中的阴影部分裁开，重新拼成梯形，其面积是；（写成多项式乘法的形式）.

(3)、由上图可以得到乘法公式；

(4)、运用得到的公式，计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ⋯ (1 - \frac{1}{10 0^{2}})$ .

查看试题解析
27. 如图1是一个长为 $4 a$ 、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）

(1)、观察图2请你写出 $(a + b)^{2}$ 、 $(a - b)^{2}$ 、 $a b$ 之间的等量关系是；

(2)、根据（1）中的结论，若 $x + y = 5 ， x \cdot y = \frac{9}{4}$ ，则 $x - y =$ ；

(3)、拓展应用：若 $(2019 - m)^{2} + (m - 2020)^{2} = 7$ ，求 $(2019 - m)$ $(m - 2020)$ 的值.

查看试题解析