2023年中考数学精选真题实战测试45 四边形综合题 A
试卷更新日期:2023-02-18 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )
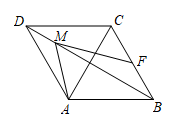 A、1 B、 C、 D、22. 如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A、1 B、 C、 D、22. 如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )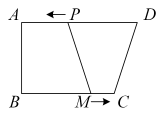 A、当时,四边形ABMP为矩形 B、当时,四边形CDPM为平行四边形 C、当时, D、当时,或6s3. 若顺次连接四边形 各边的中点所得的四边形是正方形,则四边形 的两条对角线 一定是( )A、互相平分 B、互相垂直 C、互相平分且相等 D、互相垂直且相等4. 七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,分别交BD,EF于O,P两点,M,N分别为BO,DC的中点,连接AP,NF,沿图中实线剪开即可得到一副七巧板,则在剪开之前,关于该图形,下列说法:①图中的三角形都是等腰直角三角形;②四边形MPEB是菱形;③四边形PFDM的面积占正方形ABCD面积的.正确的有( )
A、当时,四边形ABMP为矩形 B、当时,四边形CDPM为平行四边形 C、当时, D、当时,或6s3. 若顺次连接四边形 各边的中点所得的四边形是正方形,则四边形 的两条对角线 一定是( )A、互相平分 B、互相垂直 C、互相平分且相等 D、互相垂直且相等4. 七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,分别交BD,EF于O,P两点,M,N分别为BO,DC的中点,连接AP,NF,沿图中实线剪开即可得到一副七巧板,则在剪开之前,关于该图形,下列说法:①图中的三角形都是等腰直角三角形;②四边形MPEB是菱形;③四边形PFDM的面积占正方形ABCD面积的.正确的有( )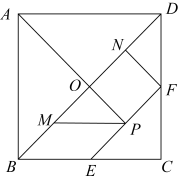 A、只有① B、①② C、①③ D、②③5. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( )
A、只有① B、①② C、①③ D、②③5. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,已知菱形的边长为2,对角线相交于点O,点M,N分别是边上的动点, , 连接.以下四个结论正确的是( )
6. 如图,已知菱形的边长为2,对角线相交于点O,点M,N分别是边上的动点, , 连接.以下四个结论正确的是( )
①是等边三角形;②的最小值是;③当最小时;④当时,.
A、①②③ B、①②④ C、①③④ D、①②③④7. 如图,已知矩形ABCD的边长分别为a,b,进行如下操作:第一次,顺次连接矩形ABCD各边的中点,得到四边形 ;第二次,顺次连接四边形 各边的中点,得到四边形 ;…如此反复操作下去,则第n次操作后,得到四边形 的面积是( ) A、 B、 C、 D、8. 如图,在矩形中, , 连接 , 分别以点 , 为圆心,大于的长为半径画弧,两弧交于点 , , 直线分别交 , 于点 , 下列结论:
A、 B、 C、 D、8. 如图,在矩形中, , 连接 , 分别以点 , 为圆心,大于的长为半径画弧,两弧交于点 , , 直线分别交 , 于点 , 下列结论:四边形是菱形;;;若平分 , 则.
其中正确结论的个数是( )
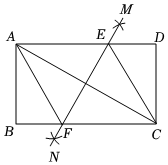 A、4 B、3 C、2 D、19. 如图,在矩形ABCD中, , ,把边AB沿对角线BD平移,点 , 分别对应点A,B.给出下列结论:①顺次连接点 , ,C,D的图形是平行四边形;②点C到它关于直线 的对称点的距离为48;③ 的最大值为15;④ 的最小值为 .其中正确结论的个数是( )
A、4 B、3 C、2 D、19. 如图,在矩形ABCD中, , ,把边AB沿对角线BD平移,点 , 分别对应点A,B.给出下列结论:①顺次连接点 , ,C,D的图形是平行四边形;②点C到它关于直线 的对称点的距离为48;③ 的最大值为15;④ 的最小值为 .其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个10. 如图, 是边长为1的等边三角形,D、E为线段AC上两动点,且 ,过点D、E分别作AB、BC的平行线相交于点F , 分别交BC、AB于点H、G . 现有以下结论:① ;②当点D与点C重合时, ;③ ;④当 时,四边形BHFG为菱形,其中正确结论为( )
A、1个 B、2个 C、3个 D、4个10. 如图, 是边长为1的等边三角形,D、E为线段AC上两动点,且 ,过点D、E分别作AB、BC的平行线相交于点F , 分别交BC、AB于点H、G . 现有以下结论:① ;②当点D与点C重合时, ;③ ;④当 时,四边形BHFG为菱形,其中正确结论为( )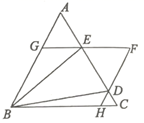 A、①②③ B、①②④ C、①②③④ D、②③④
A、①②③ B、①②④ C、①②③④ D、②③④二、填空题(每空3分,共18分)
-
11. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是矩形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=4,b=2,则矩形ABCD的面积是 .
 12. 如图,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且 , 连接EF交边AD于点G.过点A作 , 垂足为点M,交边CD于点N.若 , , 则线段AN的长为
12. 如图,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且 , 连接EF交边AD于点G.过点A作 , 垂足为点M,交边CD于点N.若 , , 则线段AN的长为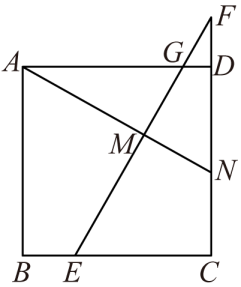 13. 如图,正方形 的对角线相交于点 ,点 在边 上,点 在 的延长线上, , 交 于点 , , ,则 .
13. 如图,正方形 的对角线相交于点 ,点 在边 上,点 在 的延长线上, , 交 于点 , , ,则 . 14. 如图,在菱形 中, ,对角线 、 相交于点 ,点 在线段 上,且 ,点 为线段 上的一个动点,则 的最小值是.
14. 如图,在菱形 中, ,对角线 、 相交于点 ,点 在线段 上,且 ,点 为线段 上的一个动点,则 的最小值是. 15. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .
15. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .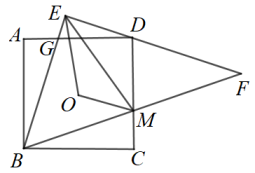 16. 如图,正方形ABCD的边长为 ,点E是BC的中点,连接CG并延长,交AB于点F , 连接AH . 以下结论:①CF⊥DE;② ;③ ,④ ,其中正确结论的序号是 .
16. 如图,正方形ABCD的边长为 ,点E是BC的中点,连接CG并延长,交AB于点F , 连接AH . 以下结论:①CF⊥DE;② ;③ ,④ ,其中正确结论的序号是 .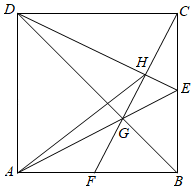
三、解答题(共7题,共72分)
-
17. 如图,在菱形ABCD中,∠BAD = 120°,AB = 6,连接BD .
 (1)、求BD的长;(2)、点E为线段BD上一动点(不与点B,D重合), 点F在边AD上,且BE=DF,
(1)、求BD的长;(2)、点E为线段BD上一动点(不与点B,D重合), 点F在边AD上,且BE=DF,①当CE丄AB时,求四边形ABEF的面积;
②当四边形ABEF的面积取得最小值时,CE+CF的值是否也最小?如果是,求CE+CF的最小值;如果不是,请说明理由.
18. 矩形ABCD中,=(k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F. (1)、【特例证明】如图(1),当k=2时,求证:AE=EF;
(1)、【特例证明】如图(1),当k=2时,求证:AE=EF;小明不完整的证明过程如下,请你帮他补充完整.
证明:如图,在BA上截取BH=BE,连接EH.
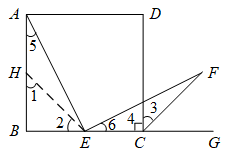
∵k=2,
∴AB=BC.
∵∠B=90°,BH=BE,
∴∠1=∠2=45°,
∴∠AHE=180°-∠1=135°.
∵CF平分∠DCG,∠DCG=90°,
∴∠3=∠DCG=45°.
∴∠ECF=∠3+∠4=135°.
∴……
(只需在答题卡对应区域写出剩余证明过程)
(2)、【类比探究】如图(2),当k≠2时,求的值(用含k的式子表示);(3)、【拓展运用】如图(3),当k=3时,P为边CD上一点,连接AP,PF,∠PAE=45°, , 求BC的长.19. 【探索发现】在一次折纸活动中,小亮同学选用了常见的A4纸,如图①,矩形为它的示意图.他查找了A4纸的相关资料,根据资料显示得出图①中 . 他先将A4纸沿过点A的直线折叠,使点B落在上,点B的对应点为点E,折痕为;再沿过点F的直线折叠,使点C落在上,点C的对应点为点H,折痕为;然后连结 , 沿所在的直线再次折叠,发现点D与点F重合,进而猜想 .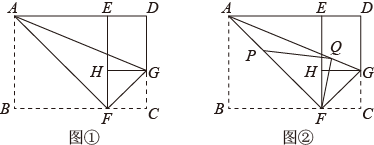 (1)、【问题解决】
(1)、【问题解决】小亮对上面的猜想进行了证明,下面是部分证明过程:
证明:四边形是矩形,
∴ .
由折叠可知, , .
∴ .
∴ .
请你补全余下的证明过程.
(2)、【结论应用】的度数为度,的值为;
(3)、在图①的条件下,点P在线段上,且 , 点Q在线段上,连结、 , 如图②,设 , 则的最小值为 . (用含a的代数式表示)20. 已知矩形ABCD,点E为直线BD上的一个动点(点E不与点B重合),连接AE,以AE为一边构造矩形AEFG(A,E,F,G按逆时针方向排列),连接DG.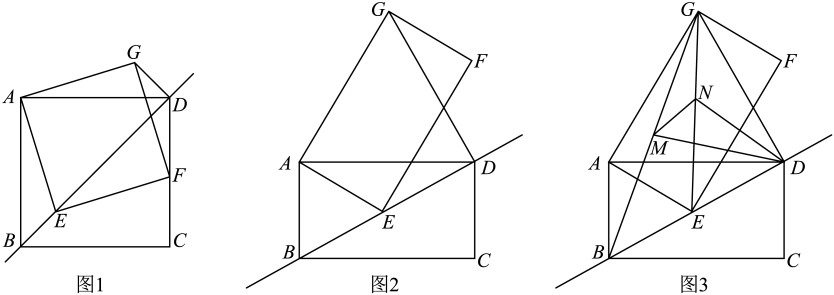 (1)、如图1,当==1时,请直接写出线段BE与线段DG的数量关系与位置关系;(2)、如图2,当==2时,请猜想线段BE与线段DG的数量关系与位置关系,并说明理由;(3)、如图3,在(2)的条件下,连接BG,EG,分别取线段BG,EG的中点M,N,连接MN,MD,ND,若AB= , ∠AEB=45°,请直接写出△MND的面积.21. 如图,矩形ABCD中,AB=15,BC=9,E是CD边上一点(不与点C重合),作AF⊥BE于F,CG⊥BE于G,延长CG至点C′,使C′G=CG,连接CF,AC′.
(1)、如图1,当==1时,请直接写出线段BE与线段DG的数量关系与位置关系;(2)、如图2,当==2时,请猜想线段BE与线段DG的数量关系与位置关系,并说明理由;(3)、如图3,在(2)的条件下,连接BG,EG,分别取线段BG,EG的中点M,N,连接MN,MD,ND,若AB= , ∠AEB=45°,请直接写出△MND的面积.21. 如图,矩形ABCD中,AB=15,BC=9,E是CD边上一点(不与点C重合),作AF⊥BE于F,CG⊥BE于G,延长CG至点C′,使C′G=CG,连接CF,AC′. (1)、直接写出图中与△AFB相似的一个三角形;(2)、若四边形AFCC′是平行四边形,求CE的长;(3)、当CE的长为多少时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形?22. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.
(1)、直接写出图中与△AFB相似的一个三角形;(2)、若四边形AFCC′是平行四边形,求CE的长;(3)、当CE的长为多少时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形?22. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.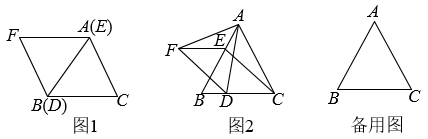 (1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.23. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.
(1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.23. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G. (1)、求证:.(2)、若 .
(1)、求证:.(2)、若 .①求菱形的面积.
②求的值.
(3)、若 , 当的大小发生变化时(),在AE上找一点T,使GT为定值,说明理由并求出ET的值.