2023年中考数学精选真题实战测试44 正方形 B
试卷更新日期:2023-02-18 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 下列命题为假命题的是( )A、对角线相等的平行四边形是矩形 B、对角线互相垂直的平行四边形是菱形 C、有一个内角是直角的平行四边形是正方形 D、有一组邻边相等的矩形是正方形2. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
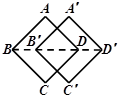 A、1cm B、2cm C、( -1)c. D、(2 -1)cm3. 如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转 ,使点B落在点 的位置,连接B ,过点D作DE⊥ ,交 的延长线于点E,则 的长为( )
A、1cm B、2cm C、( -1)c. D、(2 -1)cm3. 如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转 ,使点B落在点 的位置,连接B ,过点D作DE⊥ ,交 的延长线于点E,则 的长为( )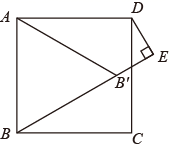 A、 B、 C、 D、4. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
A、 B、 C、 D、4. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( ) A、 B、 C、 D、5. 如图,在矩形中, , 点E,F分别在边上, , AF与相交于点O,连接 , 若 , 则与之间的数量关系正确的是( )
A、 B、 C、 D、5. 如图,在矩形中, , 点E,F分别在边上, , AF与相交于点O,连接 , 若 , 则与之间的数量关系正确的是( )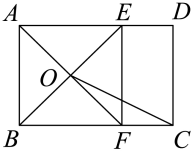 A、 B、 C、 D、6. 如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( )
A、 B、 C、 D、6. 如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( ) A、45° B、60° C、67.5° D、77.5°7. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )
A、45° B、60° C、67.5° D、77.5°7. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )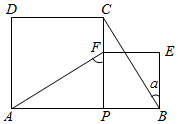 A、2α B、90°﹣α C、45°+α D、90°﹣ α8. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( )
A、2α B、90°﹣α C、45°+α D、90°﹣ α8. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( ) A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤9. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )
A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤9. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )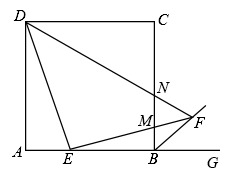 A、 B、 C、 D、110. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( )
A、 B、 C、 D、110. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题(每空3分,共18分)
-
11. 如图,正方形中,点E、F分别在边上, , 则;若的面积等于1,则的值是.
 12. 如图,在平面直角坐标系中,正方形的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数的图象经过点C,E.若点 , 则k的值是.
12. 如图,在平面直角坐标系中,正方形的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数的图象经过点C,E.若点 , 则k的值是. 13. 在综合实践课上,老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上.小红利用两张边长为2的正方形纸片,按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形.则这两个正三角形的边长分别是.14. 如图,中, , , . 四边形是正方形,点D是直线BC上一点,且 . P是线段上一点,且 . 过点P作直线l于BC平行,分别交AB,AD于点G,H,则的长是 .
13. 在综合实践课上,老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上.小红利用两张边长为2的正方形纸片,按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形.则这两个正三角形的边长分别是.14. 如图,中, , , . 四边形是正方形,点D是直线BC上一点,且 . P是线段上一点,且 . 过点P作直线l于BC平行,分别交AB,AD于点G,H,则的长是 . 15. 如图,在边长为2的正方形 中,点E,F分别为 , 边上的动点(不与端点重合),连接 , ,分别交对角线 于点P,Q.点E,F在运动过程中,始终保持 ,连接 , , .下列结论:
15. 如图,在边长为2的正方形 中,点E,F分别为 , 边上的动点(不与端点重合),连接 , ,分别交对角线 于点P,Q.点E,F在运动过程中,始终保持 ,连接 , , .下列结论:
① ;② ;③ ;④ 为等腰直角三角形;⑤若过点B作 ,垂足为H,连接 ,则 的最小值为 ,其中所有正确结论的序号是.
16. 如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为.

三、解答题(共8题,共72分)
-
17. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .
求证:四边形是正方形.
 18. 如图,点E是正方形ABCD的边BC上的动点, ,且 , .
18. 如图,点E是正方形ABCD的边BC上的动点, ,且 , .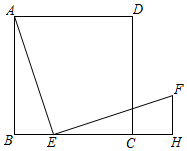 (1)、求证: ;(2)、若 , ,用x表示DF的长.19. 如图,在正方形 中,对角线 , 相交于点 ,点 , 是对角线 上的两点,且 .连接 , , , .
(1)、求证: ;(2)、若 , ,用x表示DF的长.19. 如图,在正方形 中,对角线 , 相交于点 ,点 , 是对角线 上的两点,且 .连接 , , , .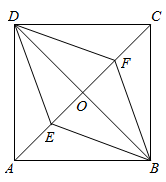 (1)、证明: .(2)、若 , ,求四边形 的周长.20. 如图,正方形 中,点E在边 上(不与端点A,D重合),点A关于直线 的对称点为点F,连接 ,设 .
(1)、证明: .(2)、若 , ,求四边形 的周长.20. 如图,正方形 中,点E在边 上(不与端点A,D重合),点A关于直线 的对称点为点F,连接 ,设 .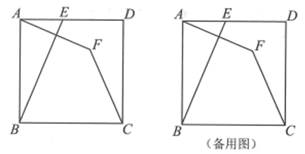 (1)、求 的大小(用含 的式子表示);(2)、过点C作 ,垂足为G,连接 .判断 与 的位置关系,并说明理由;(3)、将 绕点B顺时针旋转 得到 ,点E的对应点为点H,连接 , .当 为等腰三角形时,求 的值.21. 下面图片是八年级教科书中的一道题:如图,四边形是正方形,点是边的中点, , 且交正方形外角的平分线于点 . 求证 . (提示:取的中点 , 连接 . )
(1)、求 的大小(用含 的式子表示);(2)、过点C作 ,垂足为G,连接 .判断 与 的位置关系,并说明理由;(3)、将 绕点B顺时针旋转 得到 ,点E的对应点为点H,连接 , .当 为等腰三角形时,求 的值.21. 下面图片是八年级教科书中的一道题:如图,四边形是正方形,点是边的中点, , 且交正方形外角的平分线于点 . 求证 . (提示:取的中点 , 连接 . )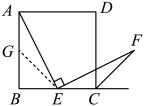 (1)、请你思考题中“提示”,这样添加辅助线的意图是得到条件:;(2)、如图1,若点是边上任意一点(不与、重合),其他条件不变.求证:;
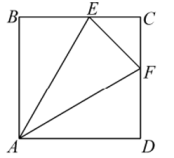
(1)、请你思考题中“提示”,这样添加辅助线的意图是得到条件:;(2)、如图1,若点是边上任意一点(不与、重合),其他条件不变.求证:;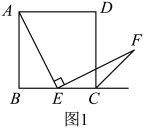 (3)、在(2)的条件下,连接 , 过点作 , 垂足为 . 设 , 当为何值时,四边形是平行四边形,并给予证明.22. 如图1,在正方形ABCD中,E,F分别是BC,CD边上的点(点E不与点B,C重合),且 .
(3)、在(2)的条件下,连接 , 过点作 , 垂足为 . 设 , 当为何值时,四边形是平行四边形,并给予证明.22. 如图1,在正方形ABCD中,E,F分别是BC,CD边上的点(点E不与点B,C重合),且 . (1)、当时,求证:;(2)、猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;(3)、如图2,连接AC,G是CB延长线上一点, , 垂足为K,交AC于点H且 . 若 , , 请用含a,b的代数式表示EF的长.23. 如图1,正方形 的边长为4,点 在边 上( 不与 重合),连接 .将线段 绕点 顺时针旋转90°得到 ,将线段 绕点 逆时针旋转90°得到 .连接 .
(1)、当时,求证:;(2)、猜想BE,EF,DF三条线段之间存在的数量关系,并证明你的结论;(3)、如图2,连接AC,G是CB延长线上一点, , 垂足为K,交AC于点H且 . 若 , , 请用含a,b的代数式表示EF的长.23. 如图1,正方形 的边长为4,点 在边 上( 不与 重合),连接 .将线段 绕点 顺时针旋转90°得到 ,将线段 绕点 逆时针旋转90°得到 .连接 .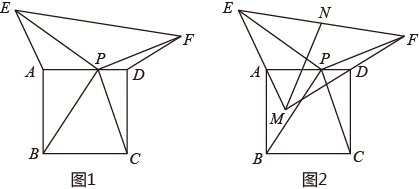 (1)、求证:
(1)、求证:① 的面积 ;
② ;
(2)、如图2, 的延长线交于点 ,取 的中点 ,连接 ,求 的取值范围.24. 已知正方形 , 为对角线 上一点.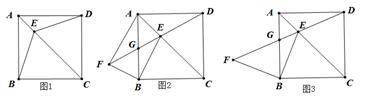 (1)、【建立模型】如图1,连接 , .求证: ;(2)、【模型应用】如图2, 是 延长线上一点, , 交 于点 .
(1)、【建立模型】如图1,连接 , .求证: ;(2)、【模型应用】如图2, 是 延长线上一点, , 交 于点 .①判断 的形状并说明理由;
②若 为 的中点,且 ,求 的长.
(3)、【模型迁移】如图3, 是 延长线上一点, , 交 于点 , .求证: .