山东省淄博市临淄区2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-02-17 类型:期中考试
一、单选题
-
1. 函数中,自变量的取值范围是( )A、 B、 C、 D、2. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,边长为1的正方形网格图中,点 , 都在格点上,若 , 则的长为( )
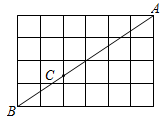 A、 B、 C、 D、5. 估计的值应在( )之间.A、3和4 B、4和5 C、5和6 D、6和76. 如果方程(m﹣3) ﹣x+3=0是关于x的一元二次方程,那么m的值为( )A、±3 B、3 C、﹣3 D、都不对7. 根据下面表格中的对应值:
A、 B、 C、 D、5. 估计的值应在( )之间.A、3和4 B、4和5 C、5和6 D、6和76. 如果方程(m﹣3) ﹣x+3=0是关于x的一元二次方程,那么m的值为( )A、±3 B、3 C、﹣3 D、都不对7. 根据下面表格中的对应值:x
3.23
3.24
3.25
3.26
ax2+bx+c
-0.06
-0.02
0.03
0.09
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A、3<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25<x<3.268. 已知多项式 , (为任意实数),试比较多项式与的大小.( )A、无法确定 B、 C、 D、9. 已知关于x的一元二次方程x2+bx﹣1=0,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关10. 已知:问题1,某厂用2年时间把总产值增加了原来的b倍,求每年平均增长的百分数;
问题2,总产值用2年的时间在原来a万元的基础上增加了b万元,求每年平均增长的百分数;
问题3,某厂用2年的时间把总产值增加到原来的b倍,求每年平均增长的百分数.
设每年平均增长的百分数x , 那么下面的三个方程:
①(1+x)2=b ,
②a(1+x)2=a+b ,
③(1+x)2=b+1,
按问题1、2、3的序号排列,相对应的是( )
A、①②③ B、③②① C、①③② D、②①③11. 若关于的一元二次方程有一根为2022,则方程必有根为( )A、2022 B、2020 C、2019 D、202112. 对于一元二次方程 , 下列说法:①若 , 则;②若方程有两个不相等的实根,则方程必有两个不相等的实根;③若c是方程的一个根,则一定有成立;④若是一元二次方程的根,则 .
其中正确的是( )
A、①②④ B、①②③ C、①③④ D、②③④二、填空题
-
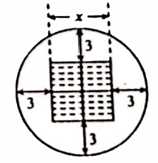
13. =.14. 若关于x的一元二次方程的两个实数根分别为2和-3,则分解因式: .15. 阅读理解:设 , , 若 , 则 , 即 , 已知 , , 且 , 则x的值为 .16. 我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池,丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑,内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形的边长是x步,则列出的方程是.
 17. 关于的方程 , , 是方程的两个根,设 , 则当的值为2时,k= .
17. 关于的方程 , , 是方程的两个根,设 , 则当的值为2时,k= .三、解答题
-
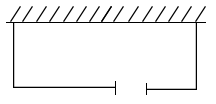
18. 计算:(1)、;(2)、 .19. 在进行二次根式化简时,我们有时会遇到如 , 这样的式子,可以将其进一步化简:; , 以上这种化简的方法叫做分母有理化.请化简下列各题(写出化简过程):(1)、;(2)、;(3)、 .20. 如图,学校建一长方形自行车棚,一边靠墙(墙长18米),另三边用总长50米的栏杆围成,留2米宽的门,若想建成面积为240平方米的自行车棚,则车棚垂直于墙的一边的长为多少米?
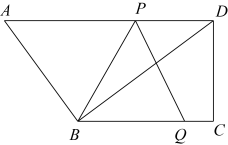
 21. 已知关于的一元二次方程 , 有两个不相等的实数根 , .(1)、求的取值范围;(2)、当时,解这个方程;(3)、若 , 是方程的两个实数根,设 , 试求的最小值.22.(1)、请用配方法解方程;(2)、请用配方法解一元二次方程 .23. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?24. 如图,在直角梯形中, , , , , . 动点从点出发,沿射线的方向以每秒2个单位的速度运动,动点从点出发,沿射线的方向以每秒1个单位的速度向点运动,点 , 分别从点 , 同时出发,当点运动到点时,点随之停止运动.设运动的时间为(秒),当为何值时,以 , , 三点为顶点的三角形是等腰三角形?
21. 已知关于的一元二次方程 , 有两个不相等的实数根 , .(1)、求的取值范围;(2)、当时,解这个方程;(3)、若 , 是方程的两个实数根,设 , 试求的最小值.22.(1)、请用配方法解方程;(2)、请用配方法解一元二次方程 .23. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?24. 如图,在直角梯形中, , , , , . 动点从点出发,沿射线的方向以每秒2个单位的速度运动,动点从点出发,沿射线的方向以每秒1个单位的速度向点运动,点 , 分别从点 , 同时出发,当点运动到点时,点随之停止运动.设运动的时间为(秒),当为何值时,以 , , 三点为顶点的三角形是等腰三角形?