山东省菏泽市定陶区2021-2022学年九年级下学期期中数学试题
试卷更新日期:2023-02-17 类型:期中考试
一、单选题
-
1. 下列各组几何体中是多面体的一组是( )A、三棱柱 四棱台 球 圆锥 B、三棱柱 四棱台 正方体 圆台 C、三棱柱 四棱台 正方体 六棱锥 D、圆锥 圆台 球 半球2. 分别写有数字-1,-2,1,3,4的五张卡片,除数字外其他均相同,将它们背面朝上,从中任抽一张,抽到负数的概率是( )A、 B、 C、 D、3. 如图的几何体由5个相同的小正方体搭成,从正面看,这个几何体的形状是( )
 A、
A、
B、
B、
C、
C、
D、
D、
4. 在Rt△ABC中,∠C=90° , BC=6,sinA= , 则AB=( )A、8 B、9 C、10 D、125. 新冠肺炎是一种传染性极强的疾病,如果有一人患病,经过两轮传染后有100人患病,设每轮传染中平均一个人传染了x个人,下列列式正确的是( )A、x+x(1+x)=100 B、1+x+x2=100 C、1+x+x(1+x)=100 D、x(1+x)=1006. 已知关于x的一元二次方程标有两个不相等的实数根,则实数k的取值范围是( )A、 B、 C、且 D、且7. 如图,已知抛物线 的图象与x轴交于 两点,其对称轴与x轴交于点C,其中 两点的横坐标分别为 和 下列说法错误的是( )
4. 在Rt△ABC中,∠C=90° , BC=6,sinA= , 则AB=( )A、8 B、9 C、10 D、125. 新冠肺炎是一种传染性极强的疾病,如果有一人患病,经过两轮传染后有100人患病,设每轮传染中平均一个人传染了x个人,下列列式正确的是( )A、x+x(1+x)=100 B、1+x+x2=100 C、1+x+x(1+x)=100 D、x(1+x)=1006. 已知关于x的一元二次方程标有两个不相等的实数根,则实数k的取值范围是( )A、 B、 C、且 D、且7. 如图,已知抛物线 的图象与x轴交于 两点,其对称轴与x轴交于点C,其中 两点的横坐标分别为 和 下列说法错误的是( )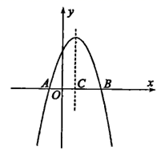 A、 B、 C、 D、当 时,y随x的增大而减小8. 如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
A、 B、 C、 D、当 时,y随x的增大而减小8. 如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 二次函数 的顶点坐标是 .10. 如图,小明从路灯下处,向前走了5米到达处,在处发现自己在地面上的影子长是2米,如果小明的身高为1.7米,那么路灯离地面的高度是米.
 11. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若圆锥的母线长l为6cm,扇形的圆心角θ=120°,则该圆锥的侧面积为cm2.(结果保留π)
11. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若圆锥的母线长l为6cm,扇形的圆心角θ=120°,则该圆锥的侧面积为cm2.(结果保留π)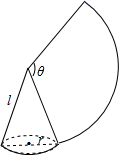 12. 如图, 的半径为2, 是 的内接三角形, ,则图中阴影部分的面积 .
12. 如图, 的半径为2, 是 的内接三角形, ,则图中阴影部分的面积 . 13. 如图,正比例函数与函数的图像交于A,B两点,轴,轴,则 .
13. 如图,正比例函数与函数的图像交于A,B两点,轴,轴,则 .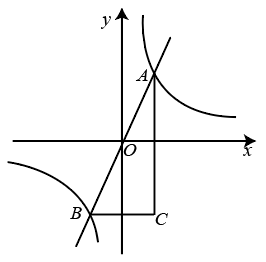 14. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …,An在x轴上,点B1 , B2 , B3 , …,Bn在直线上,若A1(1,0),且△A1B1A2 , △A2B2A3 , …,△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1 , S2 , S3 , …,Sn,则Sn可表示为 .
14. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …,An在x轴上,点B1 , B2 , B3 , …,Bn在直线上,若A1(1,0),且△A1B1A2 , △A2B2A3 , …,△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1 , S2 , S3 , …,Sn,则Sn可表示为 .
三、解答题
-
15.(1)、计算:(2)、解方程16. 如图,已知二次函数的图象过点和点 , 对称轴为直线 .
 (1)、求该二次函数的关系式和顶点坐标;(2)、结合图象,当时,直接写出x的取值范围.17. 如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)、求该二次函数的关系式和顶点坐标;(2)、结合图象,当时,直接写出x的取值范围.17. 如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数. (1)、填空: a= , b= , c=;(2)、先化简, 再求值: .18. 已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积.
(1)、填空: a= , b= , c=;(2)、先化简, 再求值: .18. 已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积. 19. 每年的4月23日是“世界读书日”,今年4月,某学校开展了以“风飘书香满校园”为主题的读书活动.活动结束后,校教导处对本校九年级学生4月份的读书量进行了随机抽样调查,并对所有随机抽取学生的读书量(单位:本)进行了统计,如图所示:
19. 每年的4月23日是“世界读书日”,今年4月,某学校开展了以“风飘书香满校园”为主题的读书活动.活动结束后,校教导处对本校九年级学生4月份的读书量进行了随机抽样调查,并对所有随机抽取学生的读书量(单位:本)进行了统计,如图所示:
根据以上信息,解答下列问题;
(1)、本次接受随机抽样调查的学生人数为 , 扇形统计图中的m的值为;(2)、本次抽取学生4月份“读书”的样本数据的众数a=本;中位数b=本;(3)、从本次调查学生中的4名同学(2男2女)随机抽取2名同学作为学校组织的“读书日”活动的主持人,求其中主持人恰好为1男1女的概率是多少?20. 一次函数y1=kx+b与反比例函数y2= (n>0)交于点A(1,3),B(3,m). (1)、分别求两个函数的解析式;(2)、根据图像直接写出,当x为何值时,y1<y2;(3)、在x轴上找一点P,使得△OAP的面积为6,求出P点坐标.21. 如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)、分别求两个函数的解析式;(2)、根据图像直接写出,当x为何值时,y1<y2;(3)、在x轴上找一点P,使得△OAP的面积为6,求出P点坐标.21. 如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.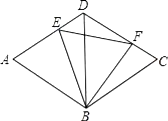 (1)、求证:△BDE≌△BCF;(2)、判断△BEF的形状,并说明理由.
(1)、求证:△BDE≌△BCF;(2)、判断△BEF的形状,并说明理由.
22. 接种疫苗是阻断新冠病毒传播的有效途径,针对疫苗急需问题,某制药厂紧急批量生产,计划每天生产疫苗16万剂,但受某些因素影响,有10名工人不能按时到厂.为了应对疫情,回厂的工人加班生产,由原来每天工作8小时增加到10小时,每人每小时完成的工作量不变,这样每天只能生产疫苗15万剂.(1)、求该厂当前参加生产的工人有多少人?(2)、生产4天后,未到的工人同时到岗加入生产,每天生产时间仍为10小时.若上级分配给该厂共760万剂的生产任务,问该厂共需要多少天才能完成任务?23. 如图,在平面直角坐标系中,抛物线 交 轴于点 ,交 轴于点 和点 ,过点 作 轴交抛物线于点 . (1)、求此抛物线的表达式;(2)、点 是抛物线上一点,且点 关于 轴的对称点在直线 上,求 的面积;(3)、若点 是直线 下方的抛物线上一动点,当点 运动到某一位置时, 的面积最大,求出此时点 的坐标和 的最大面积.
(1)、求此抛物线的表达式;(2)、点 是抛物线上一点,且点 关于 轴的对称点在直线 上,求 的面积;(3)、若点 是直线 下方的抛物线上一动点,当点 运动到某一位置时, 的面积最大,求出此时点 的坐标和 的最大面积.