山东省菏泽市单县2021-2022学年九年级下学期期中考试(一模)数学试题
试卷更新日期:2023-02-17 类型:期中考试
一、单选题
-
1. 下列各数中,比-1小的数是( )A、0 B、 C、1 D、2. 的算术平方根是( )A、4 B、±4 C、-4 D、163. 下面的几何体中,主(正)视图为三角形的是( )A、
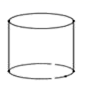 B、
B、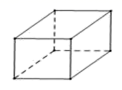 C、
C、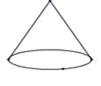 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 已知直线y=kx(k>0)与双曲线y= 交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )A、﹣6 B、﹣9 C、0 D、96. 如图,△ABC内接于半径为5的⊙O,圆心O到弦BC的距离等于3,则∠A的正切值等于( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 已知直线y=kx(k>0)与双曲线y= 交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )A、﹣6 B、﹣9 C、0 D、96. 如图,△ABC内接于半径为5的⊙O,圆心O到弦BC的距离等于3,则∠A的正切值等于( )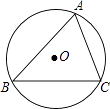 A、 B、 C、 D、7. 如图,在 中, ,由图中的尺规作图痕迹得到的射线 与 交于点E , 点F为 的中点,连接 ,若 ,则 的周长为( )
A、 B、 C、 D、7. 如图,在 中, ,由图中的尺规作图痕迹得到的射线 与 交于点E , 点F为 的中点,连接 ,若 ,则 的周长为( ) A、 B、 C、 D、48. 如图①,在正方形中,点以每秒的速度从点出发,沿的路径运动,到点停止.过点作 , 与边(或边)交于点 , 的长度与点的运动时间(秒)的函数图象如图②所示.当点运动2.5秒时,的长是( )
A、 B、 C、 D、48. 如图①,在正方形中,点以每秒的速度从点出发,沿的路径运动,到点停止.过点作 , 与边(或边)交于点 , 的长度与点的运动时间(秒)的函数图象如图②所示.当点运动2.5秒时,的长是( )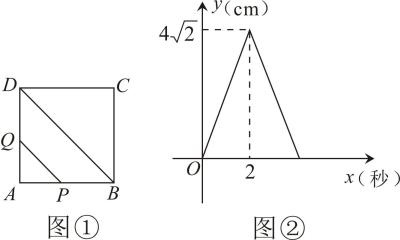 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
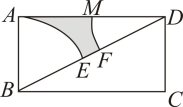
9. 分解因式: .10. 一组数据:1,2,1,0,2,a,若它们的众数为1,则这组数据的平均数为 .11. 已知抛物线与轴的一个交点为 , 则代数式的值为 .12. 如图,已知矩形中, , . 分别以 , 为圆心,为半径画弧,两弧分别交对角线于点 , , 则图中阴影部分的面积为(用含的式子表示)
 13. 如图,将边长为的正方形折叠,使点落在边的中点处,折痕为 , 点落在点处,与交于点 , 则的周长是 .
13. 如图,将边长为的正方形折叠,使点落在边的中点处,折痕为 , 点落在点处,与交于点 , 则的周长是 .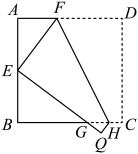 14. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.
14. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.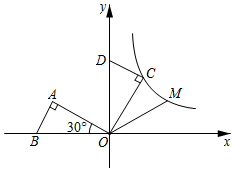
三、解答题
-
15. 计算:;16. 化简 , 再在1,2,3中选取一个适当的数代入求值.17. 如图,四边形中, , 将对角线向两端分别延长至点 , , 使 . 连接 , , 若 . 证明:四边形是平行四边形.
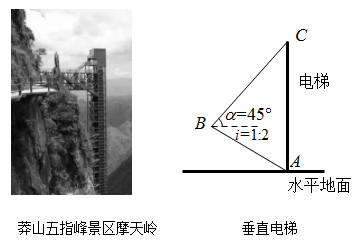
 18. 如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯的高度,测得斜坡米,坡度 , 在处测得电梯顶端的仰角 , 求观光电梯的高度.
18. 如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯的高度,测得斜坡米,坡度 , 在处测得电梯顶端的仰角 , 求观光电梯的高度.(参考数据: , , . 结果精确到0.1米)
 19. “七·一”建党节前夕,某校决定购买 , 两种奖品,用于表彰在“童心向党”活动中表现突出的学生.已知奖品比奖品每件多25元,预算资金为1700元,其中800元购买奖品,其余资金购买奖品,且购买奖品的数量是奖品的3倍.求 , 奖品的单价.20. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
19. “七·一”建党节前夕,某校决定购买 , 两种奖品,用于表彰在“童心向党”活动中表现突出的学生.已知奖品比奖品每件多25元,预算资金为1700元,其中800元购买奖品,其余资金购买奖品,且购买奖品的数量是奖品的3倍.求 , 奖品的单价.20. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.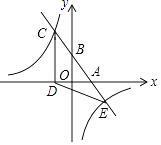 (1)、求一次函数与反比例函数的解析式;
(1)、求一次函数与反比例函数的解析式;
(2)、记两函数图象的另一个交点为E,求△CDE的面积;
(3)、直接写出不等式kx+b≤ 的解集.
21. 我市某校在推进新课改的过程中,开设的体育选修课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).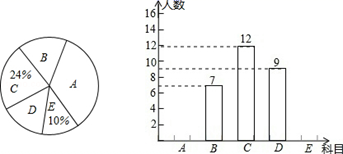 (1)、请你求出该班的总人数,并补全频数分布直方图;(2)、该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.22. 如图,在中, , 延长到点 , 以为直径作 , 交的延长线于点 , 延长到点 , 使 .
(1)、请你求出该班的总人数,并补全频数分布直方图;(2)、该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.22. 如图,在中, , 延长到点 , 以为直径作 , 交的延长线于点 , 延长到点 , 使 .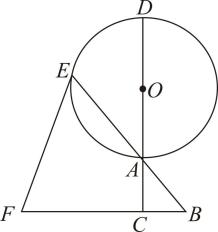 (1)、求证:是的切线;(2)、若 , , , 求的长.23. 如图1,在等腰直角三角形中, . 点 , 分别为 , 的中点,为线段上一动点(不与点 , 重合),将线段绕点逆时针方向旋转得到 , 连接 , .
(1)、求证:是的切线;(2)、若 , , , 求的长.23. 如图1,在等腰直角三角形中, . 点 , 分别为 , 的中点,为线段上一动点(不与点 , 重合),将线段绕点逆时针方向旋转得到 , 连接 , .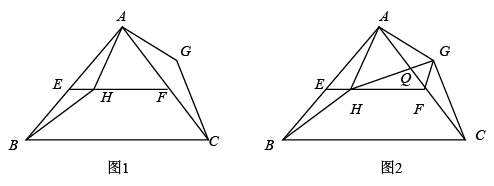 (1)、证明:;(2)、如图2,连接 , , 交于点 .
(1)、证明:;(2)、如图2,连接 , , 交于点 .①证明:在点的运动过程中,总有;
②若 , 当的长度为多少时,为等腰三角形?
24. 将抛物线向左平移1个单位,再向上平移4个单位后,得到抛物线 . 抛物线与轴交于点 , , 与轴交于点 . 已知 , 点是抛物线上的一个动点.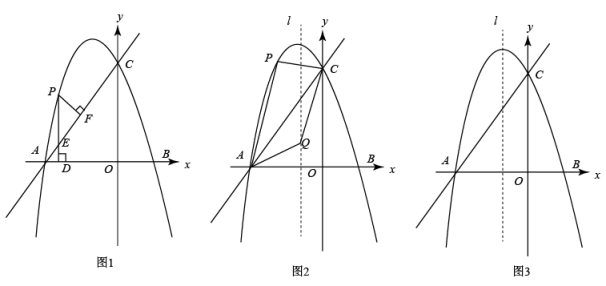 (1)、求抛物线的表达式;(2)、如图1,点在线段上方的抛物线上运动(不与 , 重合),过点作 , 垂足为 , 交于点 . 作 , 垂足为 , 求的面积的最大值;(3)、如图2,点是抛物线的对称轴上的一个动点,在抛物线上,是否存在点 , 使得以点 , , , 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点的坐标;若不存在,说明理由.
(1)、求抛物线的表达式;(2)、如图1,点在线段上方的抛物线上运动(不与 , 重合),过点作 , 垂足为 , 交于点 . 作 , 垂足为 , 求的面积的最大值;(3)、如图2,点是抛物线的对称轴上的一个动点,在抛物线上,是否存在点 , 使得以点 , , , 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点的坐标;若不存在,说明理由.