吉林省四平市2021-2022学年九年级下学期期中数学试题
试卷更新日期:2023-02-17 类型:期中考试
一、单选题
-
1. 在0,-1, , 四个数中,是无理数的是( )A、0 B、-1 C、 D、2. 如图所示的几何体的从左面看到的图形为( )
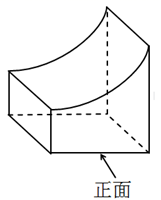 A、
A、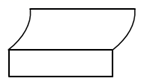 B、
B、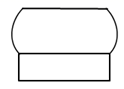 C、
C、 D、
D、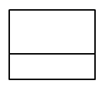 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,将矩形纸片的四个角向内翻折,恰好拼成一个无缝隙无重叠的四边形 , 若 , 则边的长是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,将矩形纸片的四个角向内翻折,恰好拼成一个无缝隙无重叠的四边形 , 若 , 则边的长是( ) A、4 B、5 C、8 D、105. 如图,在平面直角坐标系中,点P 在第一象限,⊙P与x轴相切于点Q,与y轴交于 , 两点,则点P的坐标是 ( )
A、4 B、5 C、8 D、105. 如图,在平面直角坐标系中,点P 在第一象限,⊙P与x轴相切于点Q,与y轴交于 , 两点,则点P的坐标是 ( )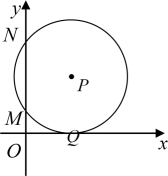 A、(5,3) B、(3,5) C、(4,5) D、(5,4)6. 如图,网格中的每个小正方形的顶点称为格点,边长均为1,的顶点均在格点上,则∠ABC的正弦值为( )
A、(5,3) B、(3,5) C、(4,5) D、(5,4)6. 如图,网格中的每个小正方形的顶点称为格点,边长均为1,的顶点均在格点上,则∠ABC的正弦值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 分解因式:m2n﹣4n=.8. 计算的结果等于 .9. 若关于x的一元二次方程(m﹣1)x2﹣2mx+(m+2)=0有实数根,则m取值范围是 .10. 已知关于x的不等式组为 , 则这个不等式组的解集为 .11. 如图,在△ABC中,AD是高,AE是角平分线,若∠B=72°,∠DAE=16°,则∠C=度.
 12. 已知 , AD与BC相交于点O.若 , AD=10,则AO= .
12. 已知 , AD与BC相交于点O.若 , AD=10,则AO= . 13. 如图.在矩形ABCD中,AB=6,BC=4,以点B为圆心,BC的长度为半径画孤,交AB于点E;以点A为圆心,AE的长度为半径画弧,交AD于点F.则图中阴影部分的面积为 . (结果保留)
13. 如图.在矩形ABCD中,AB=6,BC=4,以点B为圆心,BC的长度为半径画孤,交AB于点E;以点A为圆心,AE的长度为半径画弧,交AD于点F.则图中阴影部分的面积为 . (结果保留)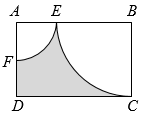 14. 如图,在平面直角坐标系中,点 , 点 , 点是第二象限内的一个动点,连接、、 , 且 , 则的最大值是 .
14. 如图,在平面直角坐标系中,点 , 点 , 点是第二象限内的一个动点,连接、、 , 且 , 则的最大值是 .
三、解答题
-
15. 某学生化简分式出现了错误,其解答过程如下:
原式=(第一步)
=(第二步)
= . (第三步)
(1)、该学生解答过程是从第步开始出错的,其错误原因是;(2)、请写出此题正确的解答过程.16. 清朝数学家梅文鼎的《方程论》中有这样一题:山田三亩,场地六亩,共折实田四亩七分;又山田五亩,场地三亩,共折实田五亩五分,问每亩山田折实田多少,每亩场地折实田多少?译文为:若有山田3亩,场地6亩,其产粮相当于实田4.7亩;若有山田5亩,场地3亩,其产粮相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?
17. “一方有难,八方支援.”2020年初武汉受到新型冠状肺炎影响,南海区某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援武汉.用树状图(或列表法)求恰好选中医生丙和护士B的概率.18. 如图,点F在平行四边形ABCD的对角线AC上,过点F,B分别作AB,AC的平行线相交于点E、连接BF;若 . 求证:四边形ABEF是菱形. 19. 图①、图②、图③均是3×3的正方形网格,每个小正方形的顶点称为格点,线段AB的端点和点P均在格点上.请按要求完成作图,保留作图痕迹.
19. 图①、图②、图③均是3×3的正方形网格,每个小正方形的顶点称为格点,线段AB的端点和点P均在格点上.请按要求完成作图,保留作图痕迹. (1)、在图①中画一条以P为端点的射线PC,使其平分线段AB,点C在线段AB上;(2)、在图②中画一条以P为端点的射线PD,使其分线段AB为1:3两部分,点D在线段AB上;(3)、在图③中画一条以P为端点的射线PE,使tan∠PEB=1,点E在线段AB上.20. 某校组织八年级全体200名学生参加“强国有我”读书活动,要求每人必读本书,活动结束后从八年级学生中随机抽查了若干名学生了解读书数量情况,并根据本;本;本;本四种类型的人数绘制了不完整的条形统计图(图1)和扇形统计图(图2).请根据统计图解答下列问题:
(1)、在图①中画一条以P为端点的射线PC,使其平分线段AB,点C在线段AB上;(2)、在图②中画一条以P为端点的射线PD,使其分线段AB为1:3两部分,点D在线段AB上;(3)、在图③中画一条以P为端点的射线PE,使tan∠PEB=1,点E在线段AB上.20. 某校组织八年级全体200名学生参加“强国有我”读书活动,要求每人必读本书,活动结束后从八年级学生中随机抽查了若干名学生了解读书数量情况,并根据本;本;本;本四种类型的人数绘制了不完整的条形统计图(图1)和扇形统计图(图2).请根据统计图解答下列问题: (1)、在这次调查中类型有多少名学生?(2)、直接写出被调查学生读书数量的众数和中位数;(3)、求被调查学生读书数量的平均数,并估计八年级200名学生共读书多少本?21. 共享单车为大众出行提供了方便,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知∠ABE=70°,∠EAB=45°,车轮半径为30cm,BE=40cm.小明体验后觉得当坐垫C离地面高度为90cm时骑着比较舒适,求此时CE的长.(结果精确到1cm)(参考数据: , , , )
(1)、在这次调查中类型有多少名学生?(2)、直接写出被调查学生读书数量的众数和中位数;(3)、求被调查学生读书数量的平均数,并估计八年级200名学生共读书多少本?21. 共享单车为大众出行提供了方便,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知∠ABE=70°,∠EAB=45°,车轮半径为30cm,BE=40cm.小明体验后觉得当坐垫C离地面高度为90cm时骑着比较舒适,求此时CE的长.(结果精确到1cm)(参考数据: , , , ) 22. 如图,四边形ABCD为正方形,点A坐标为(0,1),点B坐标为(0,﹣2),反比例函数y= 的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
22. 如图,四边形ABCD为正方形,点A坐标为(0,1),点B坐标为(0,﹣2),反比例函数y= 的图象经过点C,一次函数y=ax+b的图象经过A、C两点. (1)、求反比例函数与一次函数的解析式;(2)、若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.23. 小明从A地前往B地,同时小亮沿同一路线从B地前往A地,图1表示两人距B地的路程y(m)与行驶时间x(min)之间的函数关系.
(1)、求反比例函数与一次函数的解析式;(2)、若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.23. 小明从A地前往B地,同时小亮沿同一路线从B地前往A地,图1表示两人距B地的路程y(m)与行驶时间x(min)之间的函数关系.马小虎审题不清,将“两人距B地的路程y”看成了“两人距A地的路程y”.由此得到小明的速度为100m/min.

 (1)、A,B两地的距离为m,a=m,b=min,小明的实际速度为m/min.(2)、当时,求两人之间的距离s(m)与x(min)的函数表达式,并在图2中画出图象.24. 在▱ 中, , 平分 ,交对角线 于点G , 交射线 于点E , 将线段 绕点E顺时针旋转 得线段 .
(1)、A,B两地的距离为m,a=m,b=min,小明的实际速度为m/min.(2)、当时,求两人之间的距离s(m)与x(min)的函数表达式,并在图2中画出图象.24. 在▱ 中, , 平分 ,交对角线 于点G , 交射线 于点E , 将线段 绕点E顺时针旋转 得线段 . (1)、如图1,当 时,连接 ,请直接写出线段 和线段 的数量关系;(2)、如图2,当 时,过点B作 于点,连接 ,请写出线段 , , 之间的数量关系,并说明理由;(3)、当 时,连接 ,若 ,请直接写出 与 面积的比值.25. 如图,在平面直角坐标系中,的边OA在x轴上,OA=AB,线段OA的长是方程的根,过点B作轴,垂足为E, . 动点M以每秒1个单位长度的速度,从点A出发,沿线段AB方向向终点B运动.过点M作x轴的垂线.垂足为D、以MD为边作正方形MDCF,点C在线段OA上,设正方形MDCF与重叠部分的面积为S,点M的运动时间为秒.
(1)、如图1,当 时,连接 ,请直接写出线段 和线段 的数量关系;(2)、如图2,当 时,过点B作 于点,连接 ,请写出线段 , , 之间的数量关系,并说明理由;(3)、当 时,连接 ,若 ,请直接写出 与 面积的比值.25. 如图,在平面直角坐标系中,的边OA在x轴上,OA=AB,线段OA的长是方程的根,过点B作轴,垂足为E, . 动点M以每秒1个单位长度的速度,从点A出发,沿线段AB方向向终点B运动.过点M作x轴的垂线.垂足为D、以MD为边作正方形MDCF,点C在线段OA上,设正方形MDCF与重叠部分的面积为S,点M的运动时间为秒. (1)、求点B的坐标;(2)、当点F恰好落在OB上时,求t的值;(3)、求S关于t的函数关系式,并写出自变量t的取值范围.26. 如图①,定义:直线 与x、y轴分别相交于A、B两点,将 绕着点O逆时针旋转90°得到 ,过点A、B、D的抛物线P叫做直线 的“纠缠抛物线”,反之,直线 叫做P的“纠缠直线",两线“互为纠缠线”.
(1)、求点B的坐标;(2)、当点F恰好落在OB上时,求t的值;(3)、求S关于t的函数关系式,并写出自变量t的取值范围.26. 如图①,定义:直线 与x、y轴分别相交于A、B两点,将 绕着点O逆时针旋转90°得到 ,过点A、B、D的抛物线P叫做直线 的“纠缠抛物线”,反之,直线 叫做P的“纠缠直线",两线“互为纠缠线”.
 (1)、若 ,则纠缠物线P的函数解析式是.(2)、判断并说明 与 是否“互为纠缠线”.(3)、如图②,若纠缠直线 ,纠缠抛物线P的对称轴与 相交于点E,点F在 上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以 为一边的平行四边形时,求点Q的坐标.
(1)、若 ,则纠缠物线P的函数解析式是.(2)、判断并说明 与 是否“互为纠缠线”.(3)、如图②,若纠缠直线 ,纠缠抛物线P的对称轴与 相交于点E,点F在 上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以 为一边的平行四边形时,求点Q的坐标.