黑龙江省大庆市龙凤区2021-2022学年九年级下学期期中数学试题
试卷更新日期:2023-02-17 类型:期中考试
一、单选题
-
1. 下列各数:-4,-2.8,0, , 其中比-3小的数是( )A、-4 B、 C、0 D、-2.82. 北斗三号最后一颗全球组网卫星从西昌发射中心发射升空后,成功定点于距离地球36000千米的地球同步轨道,将“36000千米”用科学记数法表示应为( )A、米 B、米 C、米 D、米3. 2022年冬奥会将在北京举行,以下历届冬奥会会徽是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若(x+y﹣3)2与3|x﹣y﹣1|互为相反数,则yx的值是( )A、 B、1 C、2 D、45. 一个正方体沿四条棱的中点切割掉一部分后,如图所示,则该几何体的左视图是( )
4. 若(x+y﹣3)2与3|x﹣y﹣1|互为相反数,则yx的值是( )A、 B、1 C、2 D、45. 一个正方体沿四条棱的中点切割掉一部分后,如图所示,则该几何体的左视图是( )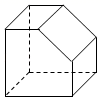 A、
A、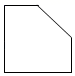 B、
B、 C、
C、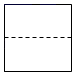 D、
D、 6. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、
6. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、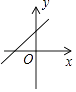 B、
B、 C、
C、 D、
D、 7. 某班级开展“好书伴成长”读书活动,统计了1至7月份该班同学每月阅读课外书的数量,绘制了折线统计图,下列说法正确的是( )
7. 某班级开展“好书伴成长”读书活动,统计了1至7月份该班同学每月阅读课外书的数量,绘制了折线统计图,下列说法正确的是( ) A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多458. 已知实数 , , 满足 , . 若 , 则的最大值为( )A、3 B、4 C、5 D、69. 在 中, , , ,点P是 所在平面内一点,则 取得最小值时,下列结论正确的是( )A、点P是 三边垂直平分线的交点 B、点P是 三条内角平分线的交点 C、点P是 三条高的交点 D、点P是 三条中线的交点10. 对于一个函数,自变量x取c时,函数值 等于0,则称c为这个函数的零点.若关于x的二次函数 有两个不相等的零点 ,关于x的方程 有两个不相等的非零实数根 ,则下列关系式一定正确的是( )A、 B、 C、 D、
A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多458. 已知实数 , , 满足 , . 若 , 则的最大值为( )A、3 B、4 C、5 D、69. 在 中, , , ,点P是 所在平面内一点,则 取得最小值时,下列结论正确的是( )A、点P是 三边垂直平分线的交点 B、点P是 三条内角平分线的交点 C、点P是 三条高的交点 D、点P是 三条中线的交点10. 对于一个函数,自变量x取c时,函数值 等于0,则称c为这个函数的零点.若关于x的二次函数 有两个不相等的零点 ,关于x的方程 有两个不相等的非零实数根 ,则下列关系式一定正确的是( )A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 若 , , 则的值为 .13. 若不等式组 无解,则m的取值范围为.14. 定义:如果一列数,从第二个数开始,每一个数与它前一个数的差都等于同一个常数,则称这列数为等差数列.如图是一个表格,其每一横行、每一竖列都成等差数列,李同学补全右侧表格后,从中任意抽取一个数字(抽后放回),连续抽取两次,则两次均为奇数的概率为 .
 15. 已知 是关于 的方程 的两个不相等实数根,且满足 ,则 的值为.16. 如图, 是⊙O的弦, ,点C是⊙O上的一个动点,且 ,若点M , N分别是 , 的中点,则图中阴影部分面积的最大值是 .
15. 已知 是关于 的方程 的两个不相等实数根,且满足 ,则 的值为.16. 如图, 是⊙O的弦, ,点C是⊙O上的一个动点,且 ,若点M , N分别是 , 的中点,则图中阴影部分面积的最大值是 .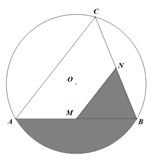 17. 在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为 , 我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”中,如图所示,点在上,且 , 若为边上一动点,当的周长最小时,则的值为 .
17. 在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为 , 我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”中,如图所示,点在上,且 , 若为边上一动点,当的周长最小时,则的值为 . 18. 函数的图象与轴交于点 , 顶点坐标为 , 其中 .
18. 函数的图象与轴交于点 , 顶点坐标为 , 其中 .①当时,则;
②若方程有两根,则;
③点 , 是抛物线上不同于 , 的两个点,当时,;
④函数的图象与的函数图象总有两个不同交点.
以上结论正确的序号是 .
三、解答题
-
19. 计算: .20. 解方程: + =21. 先化简,再求值: ,其中m是已知两边分别为2和3的三角形的第三边长,且m是整数.22. 五一期间,数学兴趣小组的几位同学到公园游玩,看到公园内宝塔耸立,几人想用所学知识测量宝塔的高度.为此,他们在距离宝塔中心18m处(AC=18m)的一个斜坡CD上进行测量.如图,已知斜坡CD的坡度为i=1: , 斜坡CD长12m,在点D处竖直放置测角仪DE,测得宝塔顶部B的仰角为37°,量得测角仪DE的高为1.5m,点A、B、C、D、E在同一平面内.
 (1)、求点D距地面的高度;(2)、求宝塔AB的高度.(结果精确到0.1,参考数据;sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,1.73)23. 某企业为推进全民健身活动,提升员工身体素质,号召员工开展健身锻炼活动,经过两个月的宣传发动,员工健身锻炼的意识有了显著提高.为了调查本企业员工上月参加健身锻炼的情况,现从1500名员工中随机抽取200人调查每人上月健身锻炼的次数,并将调查所得的数据整理如下:
(1)、求点D距地面的高度;(2)、求宝塔AB的高度.(结果精确到0.1,参考数据;sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,1.73)23. 某企业为推进全民健身活动,提升员工身体素质,号召员工开展健身锻炼活动,经过两个月的宣传发动,员工健身锻炼的意识有了显著提高.为了调查本企业员工上月参加健身锻炼的情况,现从1500名员工中随机抽取200人调查每人上月健身锻炼的次数,并将调查所得的数据整理如下:某企业员工参加健身锻炼次数的频数分布表
锻炼次数x(代号)
(A)
(B)
(C)
(D)
(E)
(F)
频数
10
a
68
c
24
6
频率
0.05
b
0.34
d
0.12
0.03
某企业员工参加健身锻炼次数的扇形统计图
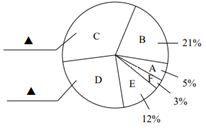 (1)、表格中 ;(2)、请把扇形统计图补充完整;(只需标注相应的数据)(3)、请估计该企业上月参加健身锻炼超过10次的员工有多少人?24. 如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)、表格中 ;(2)、请把扇形统计图补充完整;(只需标注相应的数据)(3)、请估计该企业上月参加健身锻炼超过10次的员工有多少人?24. 如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.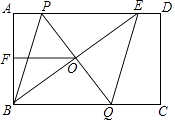 (1)、求证:四边形BPEQ是菱形;(2)、若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
(1)、求证:四边形BPEQ是菱形;(2)、若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
25. 李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程s(千米)与行驶时间t(小时)的关系如图所示(中途休息、加油的时间不计.当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升/千米,请根据图象解答下列问题: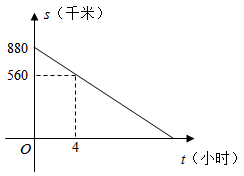 (1)、直接写出工厂离目的地的路程;(2)、求s关于t的函数表达式;(3)、当货车显示加油提醒后,问行驶时间t在怎样的范围内货车应进站加油?26. 如图,在平面直角坐标系中, 的斜边 在 轴上,坐标原点是 的中点, , ,双曲线 经过点 .
(1)、直接写出工厂离目的地的路程;(2)、求s关于t的函数表达式;(3)、当货车显示加油提醒后,问行驶时间t在怎样的范围内货车应进站加油?26. 如图,在平面直角坐标系中, 的斜边 在 轴上,坐标原点是 的中点, , ,双曲线 经过点 . (1)、求 ;(2)、直线 与双曲线 在第四象限交于点 .求 的面积.27. 如图,在中,为上一点,以点为圆心,为半径作圆,与相切于点 , 过点作交的延长线于点 , 且 .
(1)、求 ;(2)、直线 与双曲线 在第四象限交于点 .求 的面积.27. 如图,在中,为上一点,以点为圆心,为半径作圆,与相切于点 , 过点作交的延长线于点 , 且 . (1)、求证:为的切线;(2)、若 , , 求的长.28. 如图,二次函数 的图象与一次函数 的图象交于点 、 (点 在右侧),与 轴交于点 ,点 的横坐标恰好为 .动点 、 同时从原点 出发,沿射线 分别以每秒 和 个单位长度运动,经过 秒后,以 为对角线作矩形 ,且矩形四边与坐标轴平行.
(1)、求证:为的切线;(2)、若 , , 求的长.28. 如图,二次函数 的图象与一次函数 的图象交于点 、 (点 在右侧),与 轴交于点 ,点 的横坐标恰好为 .动点 、 同时从原点 出发,沿射线 分别以每秒 和 个单位长度运动,经过 秒后,以 为对角线作矩形 ,且矩形四边与坐标轴平行.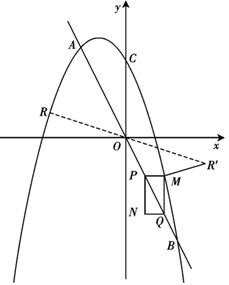 (1)、求 的值及 秒时点 的坐标;(2)、当矩形 与抛物线有公共点时,求时间 的取值范围;(3)、在位于 轴上方的抛物线图象上任取一点 ,作关于原点 的对称点为 ,当点 恰在抛物线上时,求 长度的最小值,并求此时点 的坐标.
(1)、求 的值及 秒时点 的坐标;(2)、当矩形 与抛物线有公共点时,求时间 的取值范围;(3)、在位于 轴上方的抛物线图象上任取一点 ,作关于原点 的对称点为 ,当点 恰在抛物线上时,求 长度的最小值,并求此时点 的坐标.