广东省揭阳市揭西县五校2021-2022学年九年级下学期期中考试数学试题

试卷更新日期：2023-02-17 类型：期中考试

进入出卷网下载

一、单选题

1. -2022的倒数是（）

A、2022 B、 $- \frac{1}{2022}$ C、-2022 D、 $\frac{1}{2022}$

查看试题解析
2. 2022年北京冬季奥运会的吉祥物冰墩墩、雪容融成为冬奥名副其实的顶流，实力演绎“一墩难求”，线上线下曾一度出现缺货，销量最高的一款冰墩墩雪容融手办玩具摆件销量已经超过了6万.6万用科学记数法可表示为（）

A、6×10⁵ B、0.6×10⁵ C、6×10⁴ D、0.6×10⁴

查看试题解析
3. 如图，立体图形的俯视图是（）

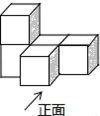A、 B、 C、 D、

查看试题解析
4. 已知一个正多边形的内角是120°，则这个正多边形的边数是（　　）

A、3 B、4 C、5 D、6

查看试题解析
5. 某小组7名学生的中考体育分数分别为 $55 ， 55 ， 57 ， 58 ， 60 ， 60 ， 60$ ，该组数据的众数和中位数分别是（）

A、60，55 B、60，58 C、55，60 D、55，57

查看试题解析
6. 分别标有数字0， $π$ ， $\frac{1}{3}$ ， -1， $\sqrt{2}$ 的五张卡片，除数字不同外其他均相同，从中任抽一张，那么抽到无理数的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
7. “清明节”期间，小海自驾去某地祭祖，如图是他们汽车行驶的路程y（千米）与汽车行驶时间x（小时）之间的函数图象．汽车行驶2小时到达目的地，这时汽车行驶了（）千米．

A、120 B、130 C、140 D、150

查看试题解析
8. 如图，在平面直角坐标系中，点P坐标为（－3，2），以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于（）

A、－5和－4之间 B、－4和－3之间 C、3和4之间 D、4和5之间

查看试题解析
9. 如图，赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为 $a$ 和 $b$ ，若 $a b = 8$ ，大正方形的边长为 $5$ ，则小正方形的面积为（）

A、9 B、3 C、12 D、13

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象如图所示，图象经过点 $(- 1 ， 0)$ ，对称轴为直线 $x = 2$ ，下列结论：① $4 a + b = 0$ ；② $9 a + c > 3 b$ ；③若点 $A (- 3 ， y_{1})$ 、点 $B (- \frac{1}{2} ， y_{2})$ 、点 $C (\frac{7}{2} ， y_{3})$ 在该函数图象上，则 $y_{1} < y_{2} < y_{3}$ ；④若方程 $a (x + 1) (x - 5) = - 3$ 的两根为 $x_{1}$ 和 $x_{2}$ ，且 $x_{1} < x_{2}$ ，则 $x_{1} < - 1 < 5 < x_{2}$ ，其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 分解因式：a²b﹣9b= ．

查看试题解析
12. 若实数m，n满足 ${(m - 6)}^{2} + \sqrt{n + 2} = 0$ ，则 $\sqrt{m + n}$ 的值是．

查看试题解析
13. 将抛物线y=-(x＋1)²＋3向右平移2个单位再向上平移2个单位后得到的新抛物线的表达式为．

查看试题解析
14. 若 $x + \frac{1}{x} = 2$ ，则 $\frac{3 x^{2} + x + 3}{x}$ 的值是.

查看试题解析
15. 如图，在 $3 \times 3$ 的方格纸中，每个小方格都是边长为1的正方形，点 $A$ 、 $B$ 、 $O$ 是格点，则图中扇形 $O A B$ 中阴影部分的面积是．

查看试题解析
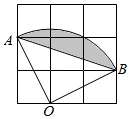16. 如图，点M是函数y= $\sqrt{3}$ x与y= $\frac{k}{x}$ 的图象在第一象限内的交点，OM=8，则k的值为．

查看试题解析
17. 如图，正方形ABCD中，AB＝2 $\sqrt{5}$ ，O是BC边的中点，点E是正方形内一动点，OE＝2，连接DE，将线段DE绕点D逆时针旋转90°得DF，连接AE、CF．则线段OF长的最小值为．

查看试题解析

三、解答题

18. 计算： ${(- 1)}^{2022} - 2 c o s 30 ° + | \sqrt{3} - 2 | - {(\sqrt{2022} - π)}^{0}$

查看试题解析
19. 如图，四边形 $A B C D$ 中， $A B ∥ C D$ ， $∠ B = ∠ D$ ，连接 $A C$ ．

(1)、尺规作图：过点 $C$ 作 $A B$ 的垂线，垂足为 $E$ （不要求写作法，保留作图痕迹）；

(2)、在（1）的条件下，已知四边形 $A B C D$ 的面积为20， $A B = 5$ ，求 $C E$ 的长．

查看试题解析
20. 学习习近平总书记关于生态文明建设重要讲话，牢固树立“绿水青山就是金山银山”的科学观，让环保理念深入到学校，某校张老师为了了解本班学生3月植树成活情况，对本班全体学生进行了调查，并将调查结果分为了三类：A：好，B：中，C：差．请根据图中信息，解答下列问题：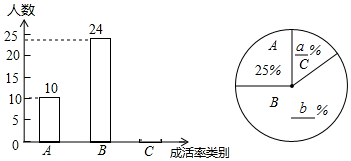

(1)、求全班学生总人数；

(2)、在扇形统计图中，a＝， b＝， C类的圆心角为；

(3)、张老师在班上随机抽取了4名学生，其中A类1人，B类2人，C类1人，若再从这4人中随机抽取2人，请求出全是B类学生的概率．

查看试题解析
21. 某学校是乒乓球体育传统项目校，为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个，已知3个甲种乒乓球和5个乙种乒乓球共需50元，2个甲种乒乓球和3个乙种乒乓球共需31元.

(1)、求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元？

(2)、学校准备购买这两种型号的乒乓球共200个，要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍，请设计出最省钱的购买方案，并说明理由.

查看试题解析
22. 如图所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连结BC．CD为⊙O的切线．

(1)、求证：BC平分∠ABD．

(2)、若∠BCD=30°，OC=6，求弧BC的长度（用含的代数式表示）．

查看试题解析
23. Rt $△$ ABC在直角坐标系内的位置如图所示，反比例函数y＝ $\frac{k}{x}$ （k≠0）在第一象限内的图象与BC边交于点D(4，1)，与AB边交于点E(2，n)．

(1)、求反比例函数的解析式和n值；

(2)、当 $\frac{B C}{A C} = \frac{1}{2}$ 时，求直线AB的解析式．

查看试题解析
24. 如图，已知E为正方形ABCD的边AD上一点，连结CE，点B关于CE的对称点为 $B^{'}$ 连结 $B^{'} D$ ，并延长 $B^{'} D$ 交BA的延长线于点F，延长CE交B′F于点G，连结BG， $B B^{'}$ ．

(1)、请写出所有与 $∠ C B G$ 相等的角（必须用图中所给的字母）；

(2)、请判断 $△ B G B^{'}$ 的形状，并证明；

(3)、若 $A E = 2 D E$ ， $B C = 6$ ，求 $B B^{'}$ 的长．

查看试题解析
25. 如图，已知抛物线 $y = a x^{2} + b x + c$ (a≠0)与x轴交于点A(－1，0)，B(4，0)，与y轴交于点C(0，2)，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为(m，0)，过点P作x轴的垂线l交抛物线于点Q．

(1)、求抛物线的解析式；

(2)、当点P在线段OB上运动时，直线l交直线BD于点M，试探究m为何值时，四边形CQMD是平行四边形；

(3)、点P在线段AB上运动过程中，是否存在点Q，使得以点B、Q、M为顶点的三角形与△BOD相似？若存在，求出点Q的坐标；若不存在，请说明理由

查看试题解析