安徽省滁州市定远县吴圩片2021-2022学年九年级下学期期中考试数学试题
试卷更新日期:2023-02-17 类型:期中考试
一、单选题
-
1. -的相反数是( )A、-2022 B、2022 C、±2022 D、2. 我省地处江、淮、汔沭泗流域下游和南北气候过渡带,滨江临海,河湖众多,地表水资源量达“264.9亿”立方米,其中264.9亿用科学记数法表示为( )A、 B、 C、 D、3. 如图,由5个完全相同的小正方体组合成的几何体,它的俯视图为( )
 A、
A、 B、
B、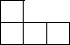 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 2012年张掖市政府投资2亿元人民币建设了廉租房8万平方米,预计2014年投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为x,根据题意,列出方程为( )A、2(1+x)2=9.5 B、2(1+x)+2(1+x)2=9.5 C、2+2(1+x)+2(1+x)2=9.5 D、2(1+x)=9.56. 估计 的值在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间7. 若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1 , x2 , 且x1≠x2 , 则m的取值范围是( )A、m>﹣ B、m<﹣ C、m≥﹣ D、m≤﹣8. 将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是( )
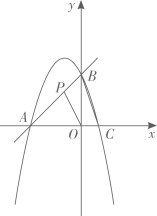
4. 下列计算正确的是( )A、 B、 C、 D、5. 2012年张掖市政府投资2亿元人民币建设了廉租房8万平方米,预计2014年投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为x,根据题意,列出方程为( )A、2(1+x)2=9.5 B、2(1+x)+2(1+x)2=9.5 C、2+2(1+x)+2(1+x)2=9.5 D、2(1+x)=9.56. 估计 的值在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间7. 若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1 , x2 , 且x1≠x2 , 则m的取值范围是( )A、m>﹣ B、m<﹣ C、m≥﹣ D、m≤﹣8. 将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是( )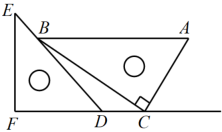 A、5 B、 C、10- D、15-9. 已知二次函数y=x2+bx-4图象上A、B两点关于原点对称,若经过A点的反比例函数的解析式是y= , 则该二次函数的对称轴是直线( )A、x=1 B、x=2 C、x=-1 D、x=-210. 如图所示,边长为2的正方形 绕点 逆时针旋转 后得到正方形 ,边 与 交于点 ,则四边形 的周长( )
A、5 B、 C、10- D、15-9. 已知二次函数y=x2+bx-4图象上A、B两点关于原点对称,若经过A点的反比例函数的解析式是y= , 则该二次函数的对称轴是直线( )A、x=1 B、x=2 C、x=-1 D、x=-210. 如图所示,边长为2的正方形 绕点 逆时针旋转 后得到正方形 ,边 与 交于点 ,则四边形 的周长( ) A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题
-
11. 计算: × = .12. 把多项式 因式分解的结果为.13. 如图,AB是半圆O的直径,AC=AD,∠CAB=20°,OE⊥CD,OE= , 则半圆O的直径AB是
 14. 已知抛物线 (k为常数,且k≤3),当-1≤x≤3时,该抛物线对应的函数值有最大值-7,则k的值为 .
14. 已知抛物线 (k为常数,且k≤3),当-1≤x≤3时,该抛物线对应的函数值有最大值-7,则k的值为 .三、解答题
-
15.(1)、计算:(2)、先化简,再求值: , 其中 .16. 如图,在边长为1的正方形网格中,△ABO的顶点均在格点上,点A,B的坐标分别是A(2,2),B(1,3),把△ABO绕点O逆时针旋转90°后得到△A1B1O.
 (1)、画出△A1B1O,直接写出点A1 , B1的坐标;(2)、求在旋转过程中,△ABO所扫过的面积.17. 已知关于x、y的方程组 中,x为非负数、y为负数.(1)、试求m的取值范围;(2)、当m取何整数时,不等式3mx+2x>3m+2的解集为x<1.18. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.19. 观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法…,据此解答下面的问题.
(1)、画出△A1B1O,直接写出点A1 , B1的坐标;(2)、求在旋转过程中,△ABO所扫过的面积.17. 已知关于x、y的方程组 中,x为非负数、y为负数.(1)、试求m的取值范围;(2)、当m取何整数时,不等式3mx+2x>3m+2的解集为x<1.18. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.19. 观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法…,据此解答下面的问题. (1)、填写下表:
(1)、填写下表:图形
挖去三角形的个数
图形1
1
图形2
1+3
图形3
1+3+9
图形4
(2)、根据这个规律,求图n中挖去三角形的个数(用含n的代数式表示);(3)、若图中挖去三角形的个数为 , 求 .20. 如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E , 连接AD , BC , CO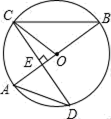 (1)、当∠BCO=25°时,求∠A的度数;(2)、若CD=4 ,BE=4,求⊙O的半径.21. 劳动教育是新时代对教育的新要求,是中国特色社会主义教育制度的重要内容,是全面发展教育体系的重要内容,是大、中、小学必须开展的教育活动.某中学为落实劳动教育,组织八年级学生进行了劳动知识技能竞赛,现随机抽取了部分同学的成绩(百分制),制成如图所示的不完整的统计图表:
(1)、当∠BCO=25°时,求∠A的度数;(2)、若CD=4 ,BE=4,求⊙O的半径.21. 劳动教育是新时代对教育的新要求,是中国特色社会主义教育制度的重要内容,是全面发展教育体系的重要内容,是大、中、小学必须开展的教育活动.某中学为落实劳动教育,组织八年级学生进行了劳动知识技能竞赛,现随机抽取了部分同学的成绩(百分制),制成如图所示的不完整的统计图表:表一
成绩x
人数
1
2
a
8
4
表二
统计量
平均数
中位数
众数
成绩
79.7
b
72

根据以上信息回答下列问题.
(1)、若抽取的学生成绩处在这一组的数据如下:88;87;81;80;82;88;84;86,根据以上数据填空:a=;b= .(2)、在扇形统计图中,表示问卷成绩在这一组的扇形圆心角度数为 .(3)、已知该校八年级共有学生500名,若将成绩不少于80分的学生称为“劳动达人”,请你估计该校八年级一共有多少名学生是“劳动达人”.