2023学年中考数学专题演练之圆、相似综合(难度指数:※※※)
试卷更新日期:2023-02-17 类型:三轮冲刺
一、圆综合专题
-
1. 如图,中, , 点在直角边上, , 点在斜边上,以点为圆心、为半径作 , 交的延长线于点 , 交于点 , 连接 , .
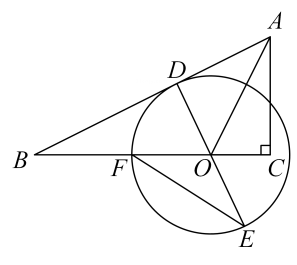 (1)、求证:为的切线;(2)、若的半径为3, , 求的长.2. 如图,四边形内接于 , 为的直径,.
(1)、求证:为的切线;(2)、若的半径为3, , 求的长.2. 如图,四边形内接于 , 为的直径,. (1)、试判断的形状,并给出证明;(2)、若 , , 求的长度.3. 如图⊙O半径为r,锐角△ABC内接于⊙O,连AO并延长交BC于D,过点D作DE⊥AC于E.
(1)、试判断的形状,并给出证明;(2)、若 , , 求的长度.3. 如图⊙O半径为r,锐角△ABC内接于⊙O,连AO并延长交BC于D,过点D作DE⊥AC于E. (1)、如图1,求证:∠DAB=∠CDE;(2)、如图1,若CD=OA,AB=6,求DE的长;(3)、如图2,当∠DAC=2∠DAB时,BD=5,DC=6,求r的值;(4)、如图3,若AE=AB=BD=1,直接写出AD+DE的值(用含r的代数式表示)4. 如图1,⊙O的直径AB=4 , C为直径AB下方半圆上一点,∠ACB的平分线交⊙O于点D,连接AD、BD.
(1)、如图1,求证:∠DAB=∠CDE;(2)、如图1,若CD=OA,AB=6,求DE的长;(3)、如图2,当∠DAC=2∠DAB时,BD=5,DC=6,求r的值;(4)、如图3,若AE=AB=BD=1,直接写出AD+DE的值(用含r的代数式表示)4. 如图1,⊙O的直径AB=4 , C为直径AB下方半圆上一点,∠ACB的平分线交⊙O于点D,连接AD、BD. (1)、判断△ABD的形状,并说明理由;(2)、如图2,点F是弧AD上一点,BF交AD于点E,求证:FE•EB=AE•DE;(3)、在(2)的条件下,若AF=0.8,求FE的长.5. 如图,已知是⊙O的直径,C为⊙O上一点,的平分线交⊙O于点D,过点D作⊙O的切线交的延长线于点E.
(1)、判断△ABD的形状,并说明理由;(2)、如图2,点F是弧AD上一点,BF交AD于点E,求证:FE•EB=AE•DE;(3)、在(2)的条件下,若AF=0.8,求FE的长.5. 如图,已知是⊙O的直径,C为⊙O上一点,的平分线交⊙O于点D,过点D作⊙O的切线交的延长线于点E.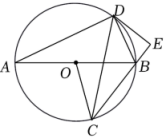 (1)、求证:;(2)、若 , , 求DE的长.6. 如图,PA切于点A,PC交于C,D两点,且与直径AB交于点Q.
(1)、求证:;(2)、若 , , 求DE的长.6. 如图,PA切于点A,PC交于C,D两点,且与直径AB交于点Q. (1)、求证:;(2)、若 , , , 求线段PD的长.7. 如图,是的直径,是弦,是的中点,弦 , H是垂足,交 , 于点F,G.
(1)、求证:;(2)、若 , , , 求线段PD的长.7. 如图,是的直径,是弦,是的中点,弦 , H是垂足,交 , 于点F,G.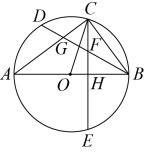 (1)、求证:;(2)、若 , , 求圆O的半径和长.8. 如图,在中, , 以为直径作 , 交边于点D,在上取一点E,使 , 连接 , 作射线交边于点F.
(1)、求证:;(2)、若 , , 求圆O的半径和长.8. 如图,在中, , 以为直径作 , 交边于点D,在上取一点E,使 , 连接 , 作射线交边于点F. (1)、求证:;(2)、若 , , 求的长.9. 如图,是的直径,点P在上,且 , 点M是外一点,与相切于点B,连接 , 过点A作交于点C,连接交于点D.
(1)、求证:;(2)、若 , , 求的长.9. 如图,是的直径,点P在上,且 , 点M是外一点,与相切于点B,连接 , 过点A作交于点C,连接交于点D. (1)、求证是的切线(2)、若 , , 连接 , 求的长.10. 阿基米德折弦定理:如图1,和是的两条弦(即折线是圆的一条折弦), , M是的中点,则从M向所作垂线的垂足D是折弦的中点,即.
(1)、求证是的切线(2)、若 , , 连接 , 求的长.10. 阿基米德折弦定理:如图1,和是的两条弦(即折线是圆的一条折弦), , M是的中点,则从M向所作垂线的垂足D是折弦的中点,即.下面是运用“截长法”证明的部分证明过程.
证明:如图2,在上截取 , 连接和.
∵M是的中点,
∴
任务:
 (1)、请按照上面的证明思路,写出该证明的剩余部分;(2)、填空:如图(3),已知等边内接于 , , D为上 一点, , 与点E,则的周长是.11. 如图1,以为直径的上有一点C,连接 , 过点B作的平分线与交于点D,过点D作的延长线于点E.
(1)、请按照上面的证明思路,写出该证明的剩余部分;(2)、填空:如图(3),已知等边内接于 , , D为上 一点, , 与点E,则的周长是.11. 如图1,以为直径的上有一点C,连接 , 过点B作的平分线与交于点D,过点D作的延长线于点E. (1)、求证:是的切线;(2)、若 , , 求的半径;(3)、如图2,过点D作于点G,求证:.
(1)、求证:是的切线;(2)、若 , , 求的半径;(3)、如图2,过点D作于点G,求证:.二、相似综合专题
-
12. 如图,在正方形ABCD中,E是边CD上的一点,F是BD上的一点,且FE=FC.
 (1)、请你判断FE是否可以由FA旋转得到,如果可以,请说明旋转方向和角度并证明;如果不可以,请说明理由;(2)、若正方形的边长为6+6,∠BAF=30°.
(1)、请你判断FE是否可以由FA旋转得到,如果可以,请说明旋转方向和角度并证明;如果不可以,请说明理由;(2)、若正方形的边长为6+6,∠BAF=30°.(i)求AF的长度;
(ii)若AE与BD交于点G,求AG的长度.
13. 在四边形中, , 为对角线, . (1)、如图1,求证:平分;(2)、如图1,求 , , 求的长;(3)、如图2,若 , E为的中点,连接、 , 与交于点F, , , 求的值.14. 如图,在正方形ABCD中,E、F分別是线段AD、AB上的点(不与端点重合),连接于点 , 连接PF.
(1)、如图1,求证:平分;(2)、如图1,求 , , 求的长;(3)、如图2,若 , E为的中点,连接、 , 与交于点F, , , 求的值.14. 如图,在正方形ABCD中,E、F分別是线段AD、AB上的点(不与端点重合),连接于点 , 连接PF. (1)、如图1,如果点是AB的中点,求证:.(2)、如图2,如果AE=AF,连接CP:
(1)、如图1,如果点是AB的中点,求证:.(2)、如图2,如果AE=AF,连接CP:①求证:;
②当 , 且的面积为4时,求的面积.
15. 如图(1)所示,在中, , D是上一点(不与A,B重合), , 交于点E,连结.设的面积为S,的面积为. (1)、当时,的面积是6,求的面积的值;(2)、当时,求S值(结果用含字母的代数式表示);(3)、如图(2)所示,在四边形中, , E是上一点(不与A,B重合), , 交于点F,连结.设 , 四边形的面积为S,的面积为 , 请你利用前面问题的解法或结论,用含字母n的代数式表示.16. 如图①,在正方形ABCD中,点P为线段BC上的一个动点,连接AP,将沿直线AP翻折得到 , 点Q是CD的中点,连接BQ交AE于点F,若.
(1)、当时,的面积是6,求的面积的值;(2)、当时,求S值(结果用含字母的代数式表示);(3)、如图(2)所示,在四边形中, , E是上一点(不与A,B重合), , 交于点F,连结.设 , 四边形的面积为S,的面积为 , 请你利用前面问题的解法或结论,用含字母n的代数式表示.16. 如图①,在正方形ABCD中,点P为线段BC上的一个动点,连接AP,将沿直线AP翻折得到 , 点Q是CD的中点,连接BQ交AE于点F,若. (1)、求证:;(2)、求证:;(3)、如图②,连接DE交BQ于点G,连接EC,GC,若 , 求的面积.17.(1)、【问题探究】
(1)、求证:;(2)、求证:;(3)、如图②,连接DE交BQ于点G,连接EC,GC,若 , 求的面积.17.(1)、【问题探究】如图①,在正方形中,点E在边AD上,点F在边CD上,且 , 线段BE与AF相交于点G,GH是的中线.

①求证:;
②试判断线段BF与GH之间的数量关系,并说明理由.
(2)、【问题拓展】如图,在矩形中, , , 点E在边AD上,点F在边CD上,且 , , 线段BE与AF相交于点G,若GH是的中线,求线段GH的长.
