初中数学同步训练必刷题(人教版八年级下册 18.1.1 平行四边形的性质)
试卷更新日期:2023-02-16 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 在同一平面内,设a、b、c是三条互相平行的直线,已知a与b间的距离为 , b与c间的距离为 , 则a与c间的距离为( )cm.A、3 B、7 C、3或7 D、2或32. 平行四边形不一定具有的特征是( )A、两组对边分别平行 B、两组对角分别相等 C、对角线相等 D、内角和为360°3. 在平行四边形ABCD中,如果 , 那么的度数是( )A、 B、 C、 D、4. 如图,平行四边形ABCD的对角线AC与BD相交于点O,AB⊥AC.若AC=6,BD=10,则AB的长是( )
 A、3 B、4 C、5 D、65. 如图,在平行四边形中,若 , 则的度数为( )
A、3 B、4 C、5 D、65. 如图,在平行四边形中,若 , 则的度数为( ) A、 B、 C、 D、6. 如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0, 2),(-1,-1)(2, -1),则顶点D的坐标是( )
A、 B、 C、 D、6. 如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0, 2),(-1,-1)(2, -1),则顶点D的坐标是( ) A、(-3, 2) B、(3, -2) C、(3, 2) D、(2, 2)7. 如图,四边形ABCD是平行四边形,点B在线段BC的延长的,若∠DCE=130°,则∠A=( )
A、(-3, 2) B、(3, -2) C、(3, 2) D、(2, 2)7. 如图,四边形ABCD是平行四边形,点B在线段BC的延长的,若∠DCE=130°,则∠A=( ) A、40° B、50° C、130° D、都不对8. 如图,在中,BE⊥CD,BF⊥AD,∠EBF=45°,CE=3,DF=1,则AF=( )
A、40° B、50° C、130° D、都不对8. 如图,在中,BE⊥CD,BF⊥AD,∠EBF=45°,CE=3,DF=1,则AF=( ) A、 B、 C、 D、9. 平行四边形相邻两角中,其中一个角的度数与另一个角的度数之间的关系是( )A、 B、 C、 D、10. 已知▱ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,不与点C重合,连接EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )
A、 B、 C、 D、9. 平行四边形相邻两角中,其中一个角的度数与另一个角的度数之间的关系是( )A、 B、 C、 D、10. 已知▱ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,不与点C重合,连接EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( ) A、①②④ B、①③ C、②③④ D、①②③④
A、①②④ B、①③ C、②③④ D、①②③④二、填空题(每题3分,共24分)
-
11. 如图所示,方格纸中每个小正方形的边长均为1,则两平行直线AB,CD之间的距离是 .
 12. 在平行四边形ABCD中,有两个内角的度数比为1:5,则平行四边形ABCD中较小内角的度数为 .13. 四边形ABCD是平行四边形,AB=8,∠BAD的平分线交直线BC于点E.若CE=2,则BC的长为 .14. 如图,在▱ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长 .
12. 在平行四边形ABCD中,有两个内角的度数比为1:5,则平行四边形ABCD中较小内角的度数为 .13. 四边形ABCD是平行四边形,AB=8,∠BAD的平分线交直线BC于点E.若CE=2,则BC的长为 .14. 如图,在▱ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长 . 15. 如图,平行四边形ABCD的面积是20,E为AB的中点,连接OE和DE,则的面积是 .
15. 如图,平行四边形ABCD的面积是20,E为AB的中点,连接OE和DE,则的面积是 . 16. 如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE= .
16. 如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE= . 17. 如图,中,对角线 , 相交于点O,交于点E,连接 , 若的周长为15,则的周长为 .
17. 如图,中,对角线 , 相交于点O,交于点E,连接 , 若的周长为15,则的周长为 . 18. 如图,在平面直角坐标系中,的顶点B在x轴上,点A坐标为 , 以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E,再分别以点D,点E为圆心,以大于的长为半径作弧,两弧在∠AOB内相交于点F,作射线OF交AC于点P.则点P的坐标是 .
18. 如图,在平面直角坐标系中,的顶点B在x轴上,点A坐标为 , 以点O为圆心,任意长为半径画弧,分别交OA,OB于点D,E,再分别以点D,点E为圆心,以大于的长为半径作弧,两弧在∠AOB内相交于点F,作射线OF交AC于点P.则点P的坐标是 .
三、解答题(共8题,共66分)
-
19. 如图,在中,对角线AC和BD相交于点O, , , . 求OB的长.
 20. 如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.
20. 如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.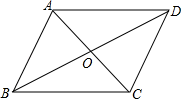 21. 如图,在中,点、在对角线上,且 , 连接、 . 求证: , .
21. 如图,在中,点、在对角线上,且 , 连接、 . 求证: , . 22. 如图,在平行四边形中,点H是边上一点,连接 .
22. 如图,在平行四边形中,点H是边上一点,连接 . (1)、尺规作图:请作出的角平分线,分别交于点G、E,交的延长线于点F.(不写作法,保留作图痕迹)(2)、若点G恰好是线段的中点,求证: .23. 如图,平行四边形ABCD中,AE平分交BC于E,DF平分交BC于F.
(1)、尺规作图:请作出的角平分线,分别交于点G、E,交的延长线于点F.(不写作法,保留作图痕迹)(2)、若点G恰好是线段的中点,求证: .23. 如图,平行四边形ABCD中,AE平分交BC于E,DF平分交BC于F. (1)、求证:;(2)、若E为BC的三等分点(靠近C点), , , 求直线AB与CD之间的距离.
(1)、求证:;(2)、若E为BC的三等分点(靠近C点), , , 求直线AB与CD之间的距离.


