初中数学同步训练必刷题（人教版七年级下册第八章二元一次方程组全章测试卷）

试卷更新日期：2023-02-16 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列属于二元一次方程的是（）

A、 $x + 2 = 2 x - 4$ B、 $3 xy + 3 = 1$ C、 $2 x = 5 y$ D、 $3 x + 2 y$

查看试题解析
2. 下列方程组中，不是二元一次方程组的是（）

A、 ${\begin{array}{l} 3 x = 0 \\ 4 x + 2 = y \end{array}$ B、 ${\begin{array}{l} 3 x - y = 6 \\ x + m = 1 \end{array}$ C、 ${\begin{array}{l} 2 x + y = 6 \\ 2 x + y = y \end{array}$ D、 ${\begin{array}{l} x^{2} + 4 x = x^{2} \\ x + y = 8 \end{array}$

查看试题解析
3. 二元一次方程组 ${\begin{array}{l} y = 2 - x \\ 3 x = 1 + 2 y \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 1 \\ y = - 1 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = 1 \end{array}$

查看试题解析
4. 已知方程组 ${\begin{array}{l} 2 x + 5 y = k \\ 7 x + 4 y = 3 k + 11 \end{array}$ 的解满足 $5 x - y = 3$ ，则k的值是（）

A、 $- 1$ B、 $- 2$ C、 $- 3$ D、 $- 4$

查看试题解析
5. 我校运动员分组训练，若每组7人，余3人；若每组8人，则缺5人，设运动员人数为 $x$ 人，组数为 $y$ 组，则列方程组为（）

A、 ${\begin{array}{l} 7 y = x - 3 \\ 8 y + 5 = x \end{array}$ B、 ${\begin{array}{l} 7 y = x + 3 \\ 8 y + 5 = x \end{array}$ C、 ${\begin{array}{l} 7 y = x - 3 \\ 8 y = x + 5 \end{array}$ D、 ${\begin{array}{l} 7 y = x + 3 \\ 8 y = x + 5 \end{array}$

查看试题解析
6. 解方程组 ${\begin{cases} 3 x - y + 2 z = 3 \\ 2 x + y - 4 z = 11 \\ 7 x + y - 5 z = 1 \end{cases}$ ，若要使运算简便，消元的方法应选取（）

A、先消去x B、先消去y C、先消去z D、以上说法都不对

查看试题解析
7. 三元一次方程组 ${\begin{array}{l} x - y = 1 \\ y - z = 1 \\ x + z = 6 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 3 \\ z = 4 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 4 \\ z = 3 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 2 \\ z = 4 \end{array}$ D、 ${\begin{array}{l} x = 4 \\ y = 3 \\ z = 2 \end{array}$

查看试题解析
8. 小明计划用100元钱在京东商城购买价格分别为6元和8元的两种商品，则在钱全部用完的前提下，可供小明选择的方案有（）

A、3种 B、4种 C、5种 D、6种

查看试题解析
9. 已知关于x，y的二元一次方程组 ${\begin{array}{l} 2 x - 5 y = 3 n + 7 \\ x - 3 y = 4 \end{array}$ 的解相等，则n的值是（）

A、3 B、 $- \frac{1}{3}$ C、1 D、 $\frac{1}{3}$

查看试题解析
10. 如图，在数轴上，点、分别表示数a、b，且a+b=2．若AB=4，则点表示的数为（）

A、-1 B、-2 C、2 D、1

查看试题解析

二、填空题(每题3分，共24分）

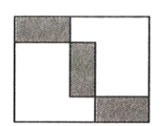
11. 写出二元一次方程 $3 x - y = 4$ 的一组解。（写出一组即可）

查看试题解析
12. 在方程 $y + 2 x = 7$ 中，用 $y$ 来表示 $x$ ，则 $x =$ .

查看试题解析
13. 已知方程组 ${\begin{array}{l} 2 x + y = 4 \\ x + 2 y = 5 \end{array}$ ，则x-y的值为．

查看试题解析
14. 若 $- 2 x^{m - n} y^{2}$ 与 $3 x^{4} y^{2 m + n}$ 是同类项，则 $m - 3 n$ 的平方根是．

查看试题解析
15. 如图，三个形状，大小都相同的小长方形沿“横—竖—横”排列在一个大长方形中，若这个大长方形的周长为2016cm，则一个小长方形的周长为cm．

查看试题解析
16. 将一张面值为50元的人民币，兑换成10元或20元的零钱，有种兑换方案．

查看试题解析
17. 若 $x + y = 3$ ， $x - y = 1$ 和 $x - 2 m y = 0$ 有公共解，则 $m$ 的值是

查看试题解析
18. 中午放学后，有a个同学在学校一食堂门口等候进食堂就餐，由于二食堂面积较大，所以配餐前二食堂等待就餐的学生人数是一食堂的2倍，开始配餐后，仍有学生继续前来排队等候就餐，设一食堂排队的学生人数按固定的速度增加，且二食堂学生人数增加的速度是一食堂的2倍，两个食堂每个窗口阿姨配餐的速度是一样的，一食堂若开放12个配餐窗口，则需10分钟才可为排队就餐的同学配餐完毕；二食堂若开放20个配餐窗口，则14分钟才可为排队就餐的同学配餐完毕；若需要在15分钟时刚好配餐完毕，则两个食堂需要同时一共开放个配餐窗口.

查看试题解析

三、解答题（共8题，共66分）

19. 解方程组

(1)、 ${\begin{matrix} 5 x + 2 y = - 3 \\ 8 x - 4 y = 9 \end{matrix}$

(2)、 ${\begin{matrix} \frac{x}{2} - \frac{y}{3} = 1 \\ 2 x + 3 y = 17 \end{matrix}$

(3)、 ${\begin{matrix} x + y - z = 0 \\ 2 x - 3 y + 2 z = 5 \\ x + 2 y - z = 3 \end{matrix}$

查看试题解析
20. 已知 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 与 ${\begin{array}{l} x = - 1 \\ y = 6 \end{array}$ 都是方程 $a x - y + b = 0$ 的解，求a、b的值．

查看试题解析
21. 已知关于 $x 、 y$ 的二元一次方程组 ${\begin{array}{l} 2 a x + y = 5 ① \\ x - b y = 2 ② \end{array}$ ．

(1)、若 $a = 1$ ，请写出方程①的所有正整数解；

(2)、由于甲看错了方程①中的 $a$ 得到方程组的解为 ${\begin{array}{l} x = - 2 \\ y = 1 \end{array}$ ，乙看错了方程②中的 $b$ 得到方程组的解为 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ ，求 $a 、 b$ 的值及原方程组的解．

查看试题解析
22. 某学校管理委员会要添置A、B两种型号的办公桌，已知购买2套A型办公桌和1套B型办公桌共需1000元，1套A型办公桌和3套B型办公桌共需1500元．求A、B两种型号的办公桌每套各是多少元？

查看试题解析
23. 今年疫情期间某物流公司计划用两种车型运输救灾物资，用2辆A型车和1辆B型车装满物资一次可运10吨；用1辆A型车和2辆B型车一次可运11吨．某物流公司现有31吨货物资，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都装满．

(1)、1辆A型车和1辆B型车都装满物资一次可分别运多少吨？

(2)、请你帮该物流公司设计租车方案，并把符合要求的租车方案都列出来；

(3)、若A型车每辆需租金每次100元，B型车每辆租金每次120元，请从（2）中的方案里选出最省钱的租车方案，并求出最少租车费．

查看试题解析

24. 【阅读理解】

在解方程组或求代数式的值时，可以用整体代入或整体求值的方法，化难为易．

（1）解方程组 ${\begin{array}{l} x + 2 (x + y) = 3 ① \\ x + y = 1 ② \end{array}$

解：（1）把②代入①得： $x + 2 \times 1 = 3 .$ 解得： $x = 1$ ．

把 $x = 1$ 代入②得： $y = 0$ ．

所以方程组的解为 ${\begin{array}{l} x = 1 \\ y = 0 \end{array}$

（2）已知 ${\begin{array}{l} 4 x + 3 y + 2 z = 10 ① \\ 9 x + 7 y + 5 z = 25 ② \end{array}$ ，求 $x + y + z$ 的值．

解：（2） $① \times 2$ 得： $8 x + 6 y + 4 z = 20 ③$

$② - ③$ 得； $x + y + z = 5$

(1)、【类比迁移】若

{\begin{array}{l} x + y + z = 18 \\ 3 x + 5 y + 7 z = 28 \end{array}

，则

2 x + 3 y + 4 z =

．

(2)、运用整体代入的方法解方程组

{\begin{array}{l} 2 x - y - 5 = 0 ① \\ \frac{2 x - y + 7}{6} + 3 y = 11 ② \end{array}

．

(3)、【实际应用】“战疫情，我们在一起”，某公益组织计划为老年公寓捐赠一批防疫物资，已知打折前购买39瓶消毒液、12支测温枪、3套防护服共需2070元；打折后购买52瓶消毒液、16支测温枪、4套防护服共需2350元，比不打折时少花了多少钱？

查看试题解析

初中数学同步训练必刷题（人教版七年级下册 第八章 二元一次方程组 全章测试卷）

一、单选题（每题3分，共30分）

二、填空题(每题3分，共24分）

三、解答题（共8题，共66分）

初中数学同步训练必刷题（人教版七年级下册第八章二元一次方程组全章测试卷）