备战2023年中考数学细点逐一突破真题训练第4章方程及方程（组）应用

试卷更新日期：2023-02-16 类型：二轮复习

进入出卷网下载

一、一元二次方程定义

1. 下列方程中，属于一元二次方程的是（）

A、 $\frac{1}{x^{2}}$ -3x+2＝0 B、2x²+y-1＝0 C、2x-3y+1＝0 D、x²- $\sqrt{2}$ x-3＝0

查看试题解析
2. 下列方程，是一元二次方程的是（）

A、 $x^{2} - \frac{1}{x} = 1$ B、 $a x^{2} + b x + c = 0$ C、 $2 x^{2} - 3 x y + 4 = 0$ D、 $x^{2} = 20$

查看试题解析
3. 一元二次方程 $2 x^{2} - 3 x - 1 = 0$ 的二次项系数和常数项分别是（）

A、2，1 B、2，0 C、2，－1 D、－3，－1

查看试题解析
4. 将方程5x²+1＝4x化成ax²+bx+c＝0的形式，则a，b，c的值分别为（）

A、5，4，1 B、5，4，-1 C、5，-4，1 D、5，-4，-1

查看试题解析

二、一元二次方程根与系数的关系

5. 已知关于x的一元二次方程 $a x^{2} - 4 x - 1 = 0$ 有两个不相等的实数根，则a的取值范围是（）

A、 $a \geq - 4$ B、 $a > - 4$ C、 $a \geq - 4$ 且 $a \neq 0$ D、 $a > - 4$ 且 $a \neq 0$

查看试题解析
6. 已知关于x的一元二次方程kx²﹣（2k﹣1）x+k﹣2＝0有两个不相等的实数根，则实数k的取值范围是（）

A、k＞﹣ $\frac{1}{4}$ B、k＜ $\frac{1}{4}$ C、k＞﹣ $\frac{1}{4}$ 且k≠0 D、k＜ $\frac{1}{4}$ 且k≠0

查看试题解析
7. 已知关于x的一元二次方程 ${(m - 1)}^{2} x^{2} + 3 m x + 3 = 0$ 有一实数根为 $- 1$ ，则该方程的另一个实数根为

查看试题解析
8. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - a = 0$ 的两根分别记为 $x_{1}$ ， $x_{2}$ ，若 $x_{1} = - 1$ ，则 $a - x_{1}^{2} - x_{2}^{2}$ 的值为（）

A、7 B、-7 C、6 D、-6

查看试题解析
9. 若实数a、b分别满足a²﹣4a+3＝0，b²﹣4b+3＝0，且a≠b，则 $\frac{1}{a} + \frac{1}{b}$ 的值为 .

查看试题解析
10. 关于x的一元二次方程2x²+4mx+m=0有两个不同的实数根x₁ ， x₂ ，且 $x_{1}^{2} + x_{2}^{2} = \frac{3}{16}$ ，则m= ．

查看试题解析

三、一元二次方程解法

11. 解方程： $(2 x + 3)^{2} = (3 x + 2)^{2}$

查看试题解析
12. 用配方法解一元二次方程 $3 x^{2} + 6 x - 1 = 0$ 时，将它化为 ${(x + a)}^{2} = b$ 的形式，则a+b的值为（）

A、 $\frac{10}{3}$ B、 $\frac{7}{3}$ C、2 D、 $\frac{4}{3}$

查看试题解析
13. 若关于x的一元二次方程x²+6x+c＝0配方后得到方程（x+3）²＝2c，则c的值为（　　）

A、﹣3 B、0 C、3 D、9

查看试题解析
14. 已知：a是不等式 $5 (a - 2) + 8 < 6 (a - 1) + 7$ 的最小整数解，请用配方法解关于x的方程 $x^{2} + 2 a x + a + 1 = 0$ .

查看试题解析
15. 一元二次方程 $x^{2} ﹣ x ﹣ 1 ＝ 0$ 的根是.

查看试题解析
16. 解方程： $3 x^{2} - 2 x - 2 = 0$ ．

查看试题解析
17. 若关于x的一元二次方程 $x^{2} - 2 m x + m^{2} - 4 m - 1 = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ，且 $(x_{1} + 2) (x_{2} + 2) - 2 x_{1} x_{2} = 17$ ，则 $m =$ （）

A、2或6 B、2或8 C、2 D、6

查看试题解析
18. 若 ${(x^{2} + y^{2})}^{2} - 5 (x^{2} + y^{2}) - 6 = 0$ ，则 $x^{2} + y^{2} =$ ．

查看试题解析
19. 若实数x，y满足 $(x + y) (x + y - 1) = 2$ ，则 $x + y$ 的值为（）

A、－1 B、2 C、－1或2 D、－2或1

查看试题解析
20. 已知实数 $x$ 满足 ${(x^{2} - 2 x + 1)}^{2} + 4 (x^{2} - 2 x + 1) - 5 = 0$ ，那么 $x^{2} - 2 x + 1$ 的值为.

查看试题解析

四、一元二次方程热点题型

21. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）

A、8 B、10 C、7 D、9

查看试题解析
22. 受国际油价影响，今年我国汽油价格总体呈上升趋势．某地92号汽油价格三月底是6.2元/升，五月底是8.9元/升．设该地92号汽油价格这两个月平均每月的增长率为 $x$ ，根据题意列出方程，正确的是（）

A、 $6.2 (1 + x)^{2} = 8.9$ B、 $8.9 (1 + x)^{2} = 6.2$ C、 $6.2 (1 + x^{2}) = 8.9$ D、 $6.2 (1 + x) + 6.2 (1 + x)^{2} = 8.9$

查看试题解析
23. 建设美丽城市，改造老旧小区.某市2019年投入资金1000万元，2021年投入资金1440万元，现假定每年投入资金的增长率相同.

(1)、求该市改造老旧小区投入资金的年平均增长率；

(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质，每个小区改造费用增加15%.如果投入资金年增长率保持不变，求该市在2022年最多可以改造多少个老旧小区？

查看试题解析
24. 网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店，销售当地农产品.其中一种当地特产在网上试销售，其成本为每千克10元.公司在试销售期间，调查发现，每天销售量y（kg）与销售单价x（元）满足如图所示的函数关系（其中 $0 < x ⩽ 30$ ）.

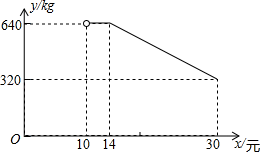(1)、直接写出y与x之间的函数关系式及自变量的取值范围.

(2)、若农贸公司每天销售该特产的利润要达到3100元，则销售单价x应定为多少元？

(3)、设每天销售该特产的利润为W元，若 $14 < x ⩽ 30$ ，求：销售单价x为多少元时，每天的销售利润最大？最大利润是多少元？

查看试题解析
25. 将一个容积为360cm³的包装盒剪开铺平，纸样如图所示．利用容积列出图中x（cm）满足的一元二次方程：（不必化简）．

查看试题解析
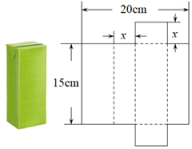26. 1275年，我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题：直田积八百六十四步，只云阔不及长一十二步.问阔及长各几步.意思是：矩形面积864平方步，宽比长少12步，问宽和长各几步.若设长为x步，则可列方程为.

查看试题解析
27. 某校“研学”活动小组在一次野外实践时，发现一种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是 $43$ ，则这种植物每个支干长出的小分支个数是（）

A、 $4$ B、 $5$ C、 $6$ D、 $7$

查看试题解析
28. 2021年7日1日建党100周年纪念日，在本月日历表上可以用一个方框圈出4个数（如图所示），若圈出的四个数中，最小数与最大数的乘积为65，求这个最小数（请用方程知识解答）．

查看试题解析
29. 某菜市场有2.5平方米和4平方米两种摊位，2.5平方米的摊位数是4平方米摊位数的2倍.管理单位每月底按每平方米20元收取当月管理费，该菜市场全部摊位都有商户经营且各摊位均按时全额缴纳管理费.

(1)、菜市场每月可收取管理费4500元，求该菜市场共有多少个4平方米的摊位？

(2)、为推进环保袋的使用，管理单位在5月份推出活动一：“使用环保袋抵扣管理费”，2.5平方米和4平方米两种摊位的商户分别有40%和20%参加了此项活动.为提高大家使用环保袋的积极性，6月份准备把活动一升级为活动二：“使用环保袋抵扣管理费”，同时终止活动一，经调查与测算，参加活动一的商户会全部参加活动二，参加活动二的商户会显著增加，这样，6月份参加活动二的2.5平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加2a%，每个摊位的管理费将会减少 $\frac{3}{10} a %$ ；6月份参加活动二的4平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加6a%，每个摊位的管理费将会减少 $\frac{1}{4} a %$ ，这样，参加活动二的这部分商户6月份总共缴纳的管理费比他们按原方式共缴纳的管理费将减少 $\frac{5}{18} a %$ ，求a的值.

查看试题解析

备战2023年中考数学细点逐一突破真题训练第4章 方程及方程（组）应用

一、一元二次方程定义

二、一元二次方程根与系数的关系

三、一元二次方程解法

四、一元二次方程热点题型

备战2023年中考数学细点逐一突破真题训练第4章方程及方程（组）应用