备战2023年中考数学细点逐一突破真题训练第3章 分式及其运算
试卷更新日期:2023-02-16 类型:二轮复习
一、分式有意义的条件
-
1. 代数式x, , , x2﹣ , , 中,属于分式的有( )A、2个 B、3个 C、4个 D、5个2. 代数式有意义时,x应满足的条件为( )A、 B、 C、 D、≤-13. 代数式 中x的取值范围在数轴上表示为( )A、
 B、
B、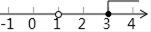 C、
C、 D、
D、 4. 若式子 有意义,则实数m的取值范围是( )A、m>﹣2 B、m>﹣2且m≠1 C、m≥﹣2 D、m≥﹣2且m≠15. 若在实数范围内有意义,则实数x的取值范围是 .6. 已知关于x的方程的解为负数,则a的取值范围是 .
4. 若式子 有意义,则实数m的取值范围是( )A、m>﹣2 B、m>﹣2且m≠1 C、m≥﹣2 D、m≥﹣2且m≠15. 若在实数范围内有意义,则实数x的取值范围是 .6. 已知关于x的方程的解为负数,则a的取值范围是 .二、分式化简及求值
-
7. 下列计算错误的是( )A、 B、 C、 D、8. 化简分式:= .9. 计算: .
三、分式化简特殊值代入
-
10. 先化简 ,然后从 ,0,1,3中选一个合适的数作为a的值代入求值.11. 先化简 ,然后从0,1,2,3中选一个合适的 值代入求解.
四、分式化简确定值代入
-
12.(1)、计算:(2)、先化简 , 再求值,其中.13. 先化简,再求值. , 其中 .14. 先化简,再求值: ,其中 , .15. 先化简,再求值:(﹣1)÷ , 其中x=﹣4.16. 若 , 则代数式的值是 .
五、分式方程含参问题
-
17. 已知关于x的分式方程的解是正数,则m的取值范围是( )A、 B、 C、且 D、且18. 若关于x的分式方程 有增根,则m的值是( )A、1 B、﹣1 C、2 D、﹣219. 若关于x的分式方程的解大于1,则m的取值范围是 .
六、分式方程及应用
-
20. 八年一班学生周末乘车去红色教育基地参观学习,基地距学校60km,一部分学生乘慢车先行,出发30min后,另一部分学生乘快车前往,结果同时到达.已知快车的速度是慢车速度的1.5倍,求慢车的速度.设慢车每小时行驶xkm,根据题意,所列方程正确的是( )A、﹣= B、﹣= C、﹣=30 D、﹣=3021. 一艘轮船在静水中的速度为30km/h,它沿江顺流航行144km与逆流航行96km所用时间相等,江水的流速为多少?设江水流速为vkm/h,则符合题意的方程是( )A、 B、 C、 D、22. 观察我国原油进口月度走势图,2022年4月原油进口量比2021年4月增加267万吨,当月增速为6.6%(计算方法:).2022年3月当月增速为 , 设2021年3月原油进口量为x万吨,下列算法正确的是( )
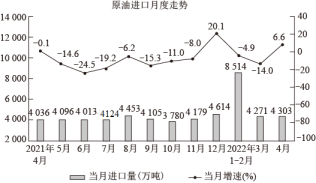 A、 B、 C、 D、23. 某农户承包的36亩水田和30亩旱地需要耕作.每天平均耕作旱地的亩数比耕作水田的亩数多4亩.该农户耕作完旱地所用的时间是耕作完水田所用时间的一半,求平均每天耕作水田的亩数.设平均每天耕作水田x亩,则可以得到的方程为( )A、 B、 C、 D、24. 在某市组织的农机推广活动中,甲、乙两人分别操控A、B两种型号的收割机参加水稻收割比赛.已知乙每小时收割的亩数比甲少40%,两人各收割6亩水稻,乙则比甲多用0.4小时完成任务;甲、乙在收割过程中对应收稻谷有一定的遗落或破损,损失率分别为3%,2%.(1)、甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻?(2)、某水稻种植大户有与比赛中规格相同的100亩待收水稻,邀请甲、乙两人操控原收割机一同前去完成收割任务,要求平均损失率不超过2.4%,则最多安排甲收割多少小时?
A、 B、 C、 D、23. 某农户承包的36亩水田和30亩旱地需要耕作.每天平均耕作旱地的亩数比耕作水田的亩数多4亩.该农户耕作完旱地所用的时间是耕作完水田所用时间的一半,求平均每天耕作水田的亩数.设平均每天耕作水田x亩,则可以得到的方程为( )A、 B、 C、 D、24. 在某市组织的农机推广活动中,甲、乙两人分别操控A、B两种型号的收割机参加水稻收割比赛.已知乙每小时收割的亩数比甲少40%,两人各收割6亩水稻,乙则比甲多用0.4小时完成任务;甲、乙在收割过程中对应收稻谷有一定的遗落或破损,损失率分别为3%,2%.(1)、甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻?(2)、某水稻种植大户有与比赛中规格相同的100亩待收水稻,邀请甲、乙两人操控原收割机一同前去完成收割任务,要求平均损失率不超过2.4%,则最多安排甲收割多少小时?