山西省2023届高三数学一模试卷

试卷更新日期：2023-02-16 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x \in N * | x^{2} \leq 4 x}$ ， $B = {x | y = \frac{1}{\sqrt{x - 3}}}$ ，则 $A \cap ∁_{R} B =$ （）

A、 $[0 ， 3]$ B、 $[1 ， 3]$ C、 ${1 ， 2}$ D、 ${1 ， 2 ， 3}$

查看试题解析
2. 复数 $z$ 满足 $| z (1 + \sqrt{3} i) | = 2$ ，则 $| z | =$ （）

A、2 B、 $\sqrt{2}$ C、1 D、 $\frac{\sqrt{2}}{2}$

查看试题解析
3. 在天文学中，常用星等 $m$ ，光照度 $E$ 等来描述天体的明暗程度.两颗星的星等与光照度满足星普森公式 $m_{2} - m_{1} = - 2.5 l g \frac{E_{2}}{E_{1}}$ .已知大犬座天狼星的星等为 $- 1.45$ ，天狼星的光照度是织女星光照度的4倍，据此估计织女星的星等为（参考数据 $l g 2 \approx 0.3$ ）（）

A、2 B、1.05 C、0.05 D、 $- 1.05$

查看试题解析
4. 经过 $A (2 ， 0)$ ， $B (0 ， 2)$ ， $C (2 ， 4)$ 三点的圆与直线 $k x - y + 2 - 4 k = 0$ 的位置关系为（）

A、相交 B、相切 C、相交或相切 D、无法确定

查看试题解析
5. 已知矩形 $A B C D$ 中， $E$ 为 $A B$ 边中点，线段 $A C$ 和 $D E$ 交于点 $F$ ，则 $\vec{B F} =$ （）

A、 $- \frac{1}{3} \vec{A B} + \frac{2}{3} \vec{A D}$ B、 $\frac{1}{3} \vec{A B} - \frac{2}{3} \vec{A D}$ C、 $\frac{2}{3} \vec{A B} - \frac{1}{3} \vec{A D}$ D、 $- \frac{2}{3} \vec{A B} + \frac{1}{3} \vec{A D}$

查看试题解析
6. 已知随机变量 $ξ_{i}$ 的分布列如下：
$ξ_{i}$
0
1
2
$P$
${(1 - p_{i})}^{2}$
$2 p_{i} (1 - p_{i})$
$p_{i}^{2}$
其中 $i = 1$ ， 2，若 $\frac{1}{2} < p_{1} < p_{2} < 1$ ，则（）

A、 $E (ξ_{1}) < E (ξ_{2})$ ， $D (3 ξ_{1} + 1) < D (3 ξ_{2} + 1)$ B、 $E (ξ_{1}) < E (ξ_{2})$ ， $D (3 ξ_{1} + 1) > D (3 ξ_{2} + 1)$ C、 $E (ξ_{1}) > E (ξ_{2})$ ， $D (3 ξ_{1} + 1) < D (3 ξ_{2} + 1)$ D、 $E (ξ_{1}) > E (ξ_{2})$ ， $D (3 ξ_{1} + 1) > D (3 ξ_{2} + 1)$

查看试题解析
7. 近年来受各种因素影响，国际大宗商品价格波动较大，我国某钢铁企业需要不间断从澳大利亚采购铁矿石，为保证企业利益最大化，提出以下两种采购方案.方案一：不考虑铁矿石价格升降，每次采购铁矿石的数量一定；方案二：不考虑铁矿石价格升降，每次采购铁矿石所花的钱数一定，则下列说法正确的是（）

A、方案一更经济 B、方案二更经济 C、两种方案一样 D、条件不足，无法确定

查看试题解析
8. 定义在 $R$ 上的函数 $f (x) = 2 s i n (ω x + \frac{π}{3}) (ω \in N *)$ 满足在区间 $(- \frac{π}{6} ， \frac{π}{6})$ 内恰有两个零点和一个极值点，则下列说法正确的是（）

A、 $f (x)$ 的最小正周期为 $\frac{π}{2}$ B、将 $f (x)$ 的图象向右平移 $\frac{π}{3}$ 个单位长度后关于原点对称 C、 $f (x)$ 图象的一个对称中心为 $(\frac{π}{6} ， 0)$ D、 $f (x)$ 在区间 $(- \frac{π}{6} ， 0)$ 上单调递增

查看试题解析

二、多选题

9. 某同学用搜集到的六组数据 $(x_{i} ， y_{i}) (i = 1 ， 2 ， ⋯ ， 6)$ 绘制了如下散点图，在这六个点中去掉 $B$ 点后重新进行回归分析，则下列说法正确的是（）

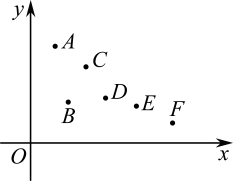A、决定系数 $R^{2}$ 变小 B、相关系数 $r$ 的绝对值越趋于1 C、残差平方和变小 D、解释变量 $x$ 与预报变量 $y$ 相关性变弱

查看试题解析
10. 设 $a > 0$ ， $b > 0$ ， $a + b = 1$ ，则下列结论正确的是（）

A、 $a b$ 的最大值为 $\frac{1}{4}$ B、 $a^{2} + b^{2}$ 的最小值为 $\frac{1}{2}$ C、 $\frac{4}{a} + \frac{1}{b}$ 的最小值为9 D、 $\sqrt{a} + \sqrt{b}$ 的最小值为 $\sqrt{3}$

查看试题解析
11. 1202年，斐波那契在《算盘全书》中从兔子问题得到斐波那契数列1，1，2，3，5，8，13，21 $⋯$ 该数列的特点是前两项为1，从第三项起，每一项都等于它前面两项的和，人们把这样的一列数组成的数列 ${a_{n}}$ 称为斐波那契数列，19世纪以前并没有人认真研究它，但在19世纪末和20世纪，这一问题派生出广泛的应用，从而活跃起来，成为热门的研究课题，记 $S_{n}$ 为该数列的前 $n$ 项和，则下列结论正确的是（）

A、 $a_{11} = 89$ B、 $a_{2023}$ 为偶数 C、 $a_{1} + a_{3} + a_{5} + ⋯ + a_{2023} = a_{2024}$ D、 $a_{2} + a_{4} + a_{6} + ⋯ + a_{2024} = S_{2023}$

查看试题解析
12. 在棱长为1的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $P$ 在侧面 $C C_{1} D_{1} D$ （含边界）内运动， $Q$ 在底面 $A B C D$ （含边界）内运动，则下列说法正确的是（）

A、若直线 $B P$ 与直线 $A D$ 所成角为30°，则 $P$ 点的轨迹为圆弧 B、若直线 $B P$ 与平面 $A B C D$ 所成角为30°，则 $P$ 点的轨迹为双曲线的一部分 C、若 $| D_{1} Q | = \frac{\sqrt{5}}{2}$ ，则 $Q$ 点的轨迹为线段 D、若 $Q$ 到直线 $D D_{1}$ 的距离等于 $Q$ 到平面 $A B B_{1} A_{1}$ 的距离，则点 $Q$ 的轨迹为抛物线的一部分

查看试题解析

三、填空题

13. 若 $f (x) = t a n x$ ，则 $f^{'} (x) =$ ．

查看试题解析
14. 已知随机变量 $X ∼ N (3 ， σ^{2})$ ，且 $P (X \leq a) = P (X \geq 4)$ ，则 ${(a x^{2} + \frac{1}{x})}^{6}$ 的展开式中常数项为.

查看试题解析
15. 写出一个同时满足下列三个条件的函数 $f (x)$ 的解析式.
① $f (1 + x) = f (1 - x)$ ；② $f (\frac{3}{2} + x) = - f (\frac{3}{2} - x)$ ；③ $f (x)$ 在 $(0 ， 1)$ 上单调递增.

查看试题解析
16. 已知抛物线 $y^{2} = 4 x$ 的焦点为 $F$ ，点 $A (4 ， 1)$ ， $P (x ， y)$ 为抛物线上一动点，则 $△ P A F$ 周长的最小值为.

查看试题解析

四、解答题

17. 在① $b (1 + c o s C) = \sqrt{3} c \cdot s i n B$ ；② ${(s i n A - \frac{1}{2} s i n B)}^{2} = s i n^{2} C - \frac{3}{4} s i n^{2} B$ ；③ $3 b c o s C + c c o s B = a + b$ 这三个条件中任选一个补充在下面的问题中，并解决该问题.
问题：在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，且____.

(1)、求角 $C$ 的大小；

(2)、若 $a = 2$ ， $b = 3$ ， $A B$ 边上一点 $P$ 满足 $| P B | = 2 | P A |$ ，求 $| P C |$ .

查看试题解析
18. 从下面的表格中选出3个数字（其中任意两个数字不同行且不同列）作为递增等差数列 ${a_{n}}$ 的前三项.

第1列
第2列
第3列
第1行
7
2
3
第2行
1
5
4
第3行
6
9
8

(1)、求数列 ${a_{n}}$ 的通项公式，并求 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ ；

(2)、若 $b_{n} = \frac{1}{a_{n}^{2}}$ ，记 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ ，求证 $T_{n} < \frac{1}{2}$ .

查看试题解析
19. 如图所示，在四棱锥 $P - A B C D$ 中，侧面 $P A D ⊥$ 平面 $A B C D$ ， $△ P A D$ 是边长为 $2$ 的等边三角形，底面 $A B C D$ 为直角梯形，其中 $B C / / A D$ ， $A B ⊥ A D$ ， $A B = B C = 1$ .

(1)、求 $B$ 到平面 $P C D$ 的距离；

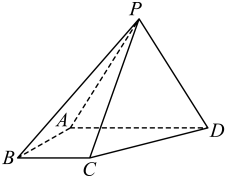(2)、线段 $P D$ 上是否存在一点 $E$ ，使得平面 $E A C$ 与平面 $D A C$ 夹角的余弦值为 $\frac{\sqrt{10}}{5}$ ？若存在，求出 $\frac{P E}{P D}$ 的值；若不存在，请说明理由.

查看试题解析
20. 假设有两个密闭的盒子，第一个盒子里装有3个白球2个红球，第二个盒子里装有2个白球4个红球，这些小球除颜色外完全相同.

(1)、每次从第一个盒子里随机取出一个球，取出的球不再放回，经过两次取球，求取出的两球中有红球的条件下，第二次取出的是红球的概率；

(2)、若先从第一个盒子里随机取出一个球放入第二个盒子中，摇匀后，再从第二个盒子里随机取出一个球，求从第二个盒子里取出的球是红球的概率.

查看试题解析
21. 双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右顶点分别为 $A$ ， $B$ ，焦点到渐近线的距离为 $\sqrt{3}$ ，且过点 $(4 ， 3)$ .

(1)、求双曲线 $C$ 的方程；

(2)、若直线 $l$ 与双曲线 $C$ 交于 $M$ ， $N$ 两点，且 $k_{A M} = - 2 k_{B N}$ ，证明直线 $l$ 过定点.

查看试题解析
22. 已知 $f (x) = x^{2} - 2 m l n x - 1$ .

(1)、若 $f (x)$ 的最小值为 $0$ ，求 $m$ 的值；

(2)、若 $a e^{x^{2} - 1} - 1 \geq 2 l n x - l n a$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析

$ξ_{i}$	0	1	2
$P$	${(1 - p_{i})}^{2}$	$2 p_{i} (1 - p_{i})$	$p_{i}^{2}$

	第1列	第2列	第3列
第1行	7	2	3
第2行	1	5	4
第3行	6	9	8