四川省资阳市安岳县2022-2023学年八年级上学期期末数学试题
试卷更新日期:2023-02-16 类型:期末考试
一、单选题
-
1. 9的算术平方根是( )A、 ﹣3 B、±3 C、3 D、2. 下列运算正确的是( )A、 B、 C、 D、3.
如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
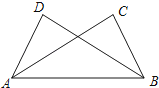 A、AC=BD B、∠CAB=∠DBA C、∠C=∠D D、BC=AD4. 学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )
A、AC=BD B、∠CAB=∠DBA C、∠C=∠D D、BC=AD4. 学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )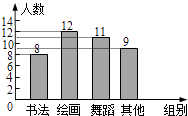 A、0.1 B、0.15 C、0.25 D、0.35. 计算的结果是( )A、 B、 C、 D、6. 已知等腰三角形的一个角为70°,则它的顶角为( )A、70° B、55° C、40° D、40°或70°7. 如图,在中, , 以顶点为圆心,适当长为半径画弧,分别交边、于点、 , 再分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是( )
A、0.1 B、0.15 C、0.25 D、0.35. 计算的结果是( )A、 B、 C、 D、6. 已知等腰三角形的一个角为70°,则它的顶角为( )A、70° B、55° C、40° D、40°或70°7. 如图,在中, , 以顶点为圆心,适当长为半径画弧,分别交边、于点、 , 再分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是( )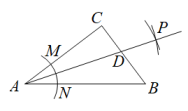 A、15 B、30 C、45 D、608. 如果 , 那么代数式的值是( )A、2020 B、2021 C、2022 D、20239. 下列说法:①“作的平分线”是命题;②命题“如果 , 那么”是真命题;③定理“等腰三角形的两底角相等”有逆定理;④若、、是的三边,且满足 , 则是直角三角形;⑤命题“同角的余角相等”可改写为“如果两个角是同一个角的余角,那么这两个角相等”.其中正确的有( )A、4个 B、3个 C、2个 D、1个10. 如图,已知在中, , , 直角的顶点P是的中点,两边、分别交、于点E、F.以下四个结论:①;②是等腰直角三角形;③;④.其中正确的是( )
A、15 B、30 C、45 D、608. 如果 , 那么代数式的值是( )A、2020 B、2021 C、2022 D、20239. 下列说法:①“作的平分线”是命题;②命题“如果 , 那么”是真命题;③定理“等腰三角形的两底角相等”有逆定理;④若、、是的三边,且满足 , 则是直角三角形;⑤命题“同角的余角相等”可改写为“如果两个角是同一个角的余角,那么这两个角相等”.其中正确的有( )A、4个 B、3个 C、2个 D、1个10. 如图,已知在中, , , 直角的顶点P是的中点,两边、分别交、于点E、F.以下四个结论:①;②是等腰直角三角形;③;④.其中正确的是( )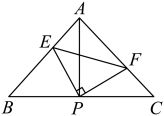 A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
11. = .12. 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有人.
 13. 若是完全平方式,则.14. 如图,在中,于点D,C是上一点, , 且点C在的垂直平分线上.若的周长为30,则的长为.
13. 若是完全平方式,则.14. 如图,在中,于点D,C是上一点, , 且点C在的垂直平分线上.若的周长为30,则的长为. 15. 如图,ABCD是长方形地面,长AB=10m,宽AD=5m,中间竖有一堵砖墙高MN=1m.一只蚂蚱从点A爬到点C,它必须翻过中间那堵墙,则它至少要走m.
15. 如图,ABCD是长方形地面,长AB=10m,宽AD=5m,中间竖有一堵砖墙高MN=1m.一只蚂蚱从点A爬到点C,它必须翻过中间那堵墙,则它至少要走m.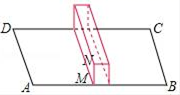 16. 观察下列各式及其展开式:
16. 观察下列各式及其展开式:…
请你猜想的展开式第三项的系数是 .
三、解答题
-
17.(1)、计算:(2)、分解因式:18. 先化简,再求值:
, 其中、满足.
19. 为深化课程改革,某校为学生开设了形式多样的社团课程.为了了解部分社团课程在学生中最受欢迎的程度,学校随机抽取八年级名学生进行调查,从A:文学鉴赏,B:科学探究,C:文史天地, D:趣味数学四门课程中选出你最喜欢的课程(被调查的每名学生必选且只能选择一门课程),并将调查结果绘制成两个不完整的统计图,如图所示, (1)、= 人,= ;(2)、扇形统计图中,“D”所对的扇形的圆心角是 ▲ , 并补全条形统计图;(3)、根据本次调查,该校八年级1240名学生中,估计最喜欢“科学探究”的学生人数为多少?20. 如图,P是等边内的一点,连接 , 以为边作 , 且 , 连接.若 , 连接.
(1)、= 人,= ;(2)、扇形统计图中,“D”所对的扇形的圆心角是 ▲ , 并补全条形统计图;(3)、根据本次调查,该校八年级1240名学生中,估计最喜欢“科学探究”的学生人数为多少?20. 如图,P是等边内的一点,连接 , 以为边作 , 且 , 连接.若 , 连接.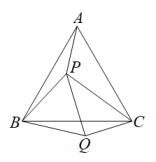 (1)、证明:;(2)、求的度数.21. 如图,在中, , 把沿直线折叠,使与重合.
(1)、证明:;(2)、求的度数.21. 如图,在中, , 把沿直线折叠,使与重合. (1)、若 , 则的度数为;(2)、当 , 的面积为时,的周长为(用含的代数式表示);(3)、若 , , 求的长.22. 定义:一个三位正整数,如果十位数字恰好等于百位数字与个位数字之和的一半,我们称这个三位正整数为“半和数”.例如三位正整数234中, , 所以,234是半和数;又如369中, , 所以,369也是半和数.…
(1)、若 , 则的度数为;(2)、当 , 的面积为时,的周长为(用含的代数式表示);(3)、若 , , 求的长.22. 定义:一个三位正整数,如果十位数字恰好等于百位数字与个位数字之和的一半,我们称这个三位正整数为“半和数”.例如三位正整数234中, , 所以,234是半和数;又如369中, , 所以,369也是半和数.…任务:
(1)、已知一个三位数是“半和数”,若它的百位数字是7,个位数字是1,则这个数是;若它的百位数字为a,个位数字为0,则十位数字为;这个数为;(用含a的代数式表示);(2)、任意一个“半和数”的个位和百位数字调换得到一个新“半和数”,然后将新“半和数”与原“半和数”相加,结果是的倍数.请你判断这一结论是否正确,并说明理由.23. 若满足 , 求的值.解:设 , , 则 , , .
(1)、若满足 , 求的值;(2)、
【拓展应用】
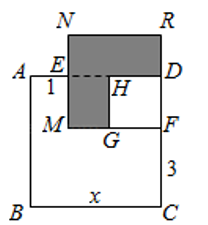
如图,已知正方形的边长为分别是上的点,且 , 长方形的面积是 , 分别以为边作正方形.① ▲ , ▲ ;(用含的式子表示)
②求阴影部分的面积.
 24. 如图1,在中,为锐角,点为射线上一点,连接 , 以为一边且在的右侧作正方形 , 连接.
24. 如图1,在中,为锐角,点为射线上一点,连接 , 以为一边且在的右侧作正方形 , 连接.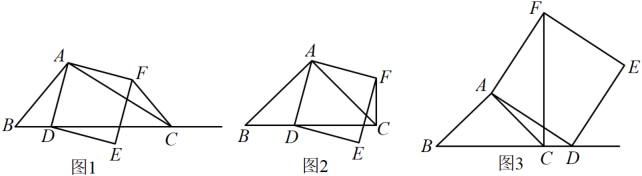 (1)、如果 ,
(1)、如果 ,①当点在线段上时(与点不重合),如图2,线段 , 所在直线的位置关系为 ▲ , 线段 , 的数量关系为 ▲ ;
②当点在线段的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)、如果 , 是锐角,点在线段上,当满足什么条件时,(点、不重合),请直接写出答案.