四川省资阳市安岳县2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-16 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 下列事件为必然事件的是( )A、篮球运动员在罚球线上投篮一次,未投中 B、在数轴上任取一点,则该点表示的数是有理数 C、经过有交通信号灯的路口,遇到绿灯 D、任意画一个四边形,其内角和为360°3. 估算:的值应在( )A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间4. 在平面直角坐标系中,将点向右平移1个单位,再向下平移2个单位,得到的点的坐标为( )A、 B、 C、 D、5. 如图,在中,D、E、F分别是、、的中点,若 , 则的度数为( )
 A、 B、 C、 D、6. “读万卷书,行万里路.”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x,则可列方程为( )A、 B、 C、 D、7. 如图,在四边形中,与相交于点O,若 , 则的值为( )
A、 B、 C、 D、6. “读万卷书,行万里路.”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x,则可列方程为( )A、 B、 C、 D、7. 如图,在四边形中,与相交于点O,若 , 则的值为( ) A、 B、 C、 D、8. 已知实数a在数轴上的位置如图所示,则化简:的结果为( )
A、 B、 C、 D、8. 已知实数a在数轴上的位置如图所示,则化简:的结果为( )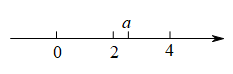 A、2 B、-2 C、2a-6 D、-2a+69. 如图,在菱形中, , E是上一点,连接 , 将沿AE翻折,使点B落在点F处,连接.若 , 则的值为( )
A、2 B、-2 C、2a-6 D、-2a+69. 如图,在菱形中, , E是上一点,连接 , 将沿AE翻折,使点B落在点F处,连接.若 , 则的值为( ) A、 B、 C、 D、10. 如图,直线l的解析式为 , 点 , 轴交直线l于点;点为y轴上位于上方的一点,且 , 轴交直线l于点;点为y轴上位于上方的一点,且 , 轴交直线l于点 , 按此规律,线段的长为( )
A、 B、 C、 D、10. 如图,直线l的解析式为 , 点 , 轴交直线l于点;点为y轴上位于上方的一点,且 , 轴交直线l于点;点为y轴上位于上方的一点,且 , 轴交直线l于点 , 按此规律,线段的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 使代数式 有意义的x的取值范围是 .12. 如图所示的电路中,若任意闭合一个开关,则灯泡L1发光的概率是.
 13. 若最简二次根式与是同类二次根式,则m =.14. 若 , 且 , 则的值为.15. 如图,在中,为边上的中线,点G为的重心.若 , 则的长为.
13. 若最简二次根式与是同类二次根式,则m =.14. 若 , 且 , 则的值为.15. 如图,在中,为边上的中线,点G为的重心.若 , 则的长为. 16. 如图1,在四边形中,若 , 则称为四边形关于点A的“靓线”.如图2,在中, , E为的中点,F为延长线上一点,连结 , 若BE为四边形关于点B的“靓线”, , 则的长为.
16. 如图1,在四边形中,若 , 则称为四边形关于点A的“靓线”.如图2,在中, , E为的中点,F为延长线上一点,连结 , 若BE为四边形关于点B的“靓线”, , 则的长为.

三、解答题
-
17. 计算:(1)、(2)、18. 先化简,再求值: , 其中.19. 如图,已知:三个顶点的坐标分别为 , , .

⑴画出关于x轴对称的;
⑵以点O为位似中心,将放大为原来的2倍,得到 , 请在网格中画出 , 并写出点的坐标.
20. 为了更好落实“双减”政策,增强课后服务的时效性,我县一中学定于每周四下午进行兴趣课“走班制”,开设了5类兴趣课(每位学生均选其一):A.音乐;B.体育;C.美术;D.信息技术;E.演讲.为了了解该校学生的参与情况,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
(1)、求此次调查的学生人数,并补全条形统计图;(2)、求“C”类兴趣课所对应扇形的圆心角的度数;(3)、若“E”类兴趣班中有2名男生和3名女生,从中随机抽取2名参加县级演讲比赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.21. 第19届亚运会原定于2022年9月10日至25日在杭州举行,其吉祥物“琼琼”、“莲莲”、“宸宸”组成的“江南忆”毛绒玩具套件,已成为杭州店销人气款.某商场销售这种毛绒玩具,平均每天可售出50套,每套盈利60元.但由于受疫情影响,此届亚运会将延期至2023年举行,于是该商场决定采取降价措施,以尽快减少库存,经调查发现,每套毛绒玩具每降价1元,平均每天可多售出2套.(1)、若每套毛绒玩具降价5元,则该商场平均每天可盈利多少元?(2)、若该商场计划平均每天盈利3500元,则每套毛绒玩具应降价多少元?22. 如图,A、B两地是我国某海域一东西方向上的两个小岛.一天,一艘渔政船在C处巡逻时,测得小岛A在它的北偏东方向上,它沿西北方向航行海里后到达D处,测得小岛A在它的东北方向. (1)、求D处与小岛A的距离;(2)、若该渔政船在D处测得小岛B在它的北偏西方向上,求小岛A、B之间的距离.(参考数据: , , )23. 定义:已知是关于x的一元二次方程的两个实数根,若 , 且 , 则称这个方程为“限根方程”.如:一元二次方程的两根为 , 因 , , 所以一元二次方程为“限根方程”.
(1)、求D处与小岛A的距离;(2)、若该渔政船在D处测得小岛B在它的北偏西方向上,求小岛A、B之间的距离.(参考数据: , , )23. 定义:已知是关于x的一元二次方程的两个实数根,若 , 且 , 则称这个方程为“限根方程”.如:一元二次方程的两根为 , 因 , , 所以一元二次方程为“限根方程”.请阅读以上材料,回答下列问题:
(1)、判断一元二次方程是否为“限根方程”,并说明理由;(2)、若关于x的一元二次方程是“限根方程”,且两根满足 , 求k的值;(3)、若关于x的一元二次方程是“限根方程”,求m的取值范围.24. 【情境再现】 (1)、如图1,在正方形中,点E、F分别在边上,且 , 求证:.(2)、【迁移应用】
(1)、如图1,在正方形中,点E、F分别在边上,且 , 求证:.(2)、【迁移应用】
如图2,在矩形中,(k为常数),点E、F、G、H分别在矩形的边上,且 , 求证:.(3)、【拓展延伸】
如图3,在四边形中, , , , 点E、F分别在边上,且 , , 求的长.