四川省内江市2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-02-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，是关于x的一元二次方程的是（）

A、 $π x = 6$ B、 $x - \frac{3}{x} = 2$ C、 $x y = 1$ D、 $x^{2} + 5 x = 6$

查看试题解析
2. 下列各式中正确的是（）

A、 $\sqrt{36}$ ＝±6 B、 $\sqrt{{(- 2)}^{- 2}} = - 2$ C、 $\sqrt{8}$ ＝4 D、 ${(- \sqrt{7})}^{2}$ ＝7

查看试题解析
3. 下列事件中属于随机事件的是（）

A、今天是星期一，明天是星期二 B、从一个装满红球的袋子里摸出了一个白球 C、掷一枚质地均匀的硬币正面朝上 D、抛出的篮球会下落

查看试题解析
4. 若 $\frac{m}{n} = \frac{2}{3}$ ，则 $\frac{m + n}{n}$ 等于（）

A、 $\frac{5}{3}$ B、 $\frac{3}{5}$ C、 $\frac{2}{3}$ D、1

查看试题解析
5. 若式子 $\frac{\sqrt{x - 2}}{x - 3}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \geq 2$ B、 $x \neq 3$ C、 $x \geq 2$ 或 $x \neq 3$ D、 $x \geq 2$ 且 $x \neq 3$

查看试题解析
6. 在 $△ A B C$ 中， $∠ C = 90 °$ ，若 $s i n A = \frac{1}{2}$ ，则 $c o s B$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、2 D、 $\frac{\sqrt{3}}{2}$

查看试题解析
7. 新冠肺炎是一种传染性极强的疾病，如果有一人患病，经过两轮传染后有64人患病，设每轮传染中平均一个人传染了x个人，下列列式正确的是（）

A、 $x + x (1 + x) = 64$ B、 $1 + x + x^{2} = 64$ C、 $(1 + x)^{2} = 64$ D、 $x (1 + x) = 64$

查看试题解析
8. 如图， $△ A B C$ 与 $△ D E F$ 是位似图形，点 $O$ 是位似中心，若 $O A ： A D = 1 ： 2$ ，且 $△ A B C$ 的面积为2，则 $△ D E F$ 的面积为（）

A、6 B、9 C、18 D、27

查看试题解析
9. 已知方程 $x^{2} + 2019 x - 3 = 0$ 的两根分别是 $α$ 和 $β$ ，则代数式 $α^{2} + α β + 2019 α$ 的值为（）

A、1 B、0 C、2019 D、-2019

查看试题解析
10. 如图，直立于地面上的电线杆 $A B$ ，在阳光下落在水平地面和坡面上的影子分别是 $B C$ 、 $C D$ ，坡面的坡度 $t = 1 ： \sqrt{3}$ ，测得 $B C = 6$ 米， $C D = 4$ 米，在D处测得电线杆顶端A的仰角为 $30 °$ ，则电线杆 $A B$ 的高度为（）米.

A、 $2 + 2 \sqrt{3}$ B、 $4 + 2 \sqrt{3}$ C、 $2 + 3 \sqrt{2}$ D、 $4 + 3 \sqrt{2}$

查看试题解析
11. 如图，△ABC的面积为1，分别取AC、BC两边的中点A₁、B₁ ，则四边形A₁ABB₁的面积为 $\frac{3}{4}$ ，再分别取A₁C、B₁C的中点A₂、B₂ ，取A₂C、B₂C的中点A₃、B₃ ，依次取下去…利用这一图形，能直观地计算出 $\frac{3}{4} + \frac{3}{4^{2}} + \frac{3}{4^{3}} + ⋯ + \frac{3}{4^{n}} =$ （）

A、1 B、 $\frac{4^{n - 1}}{4^{n}}$ C、 $1 - \frac{1}{4^{n}}$ D、 $\frac{4^{n} + 1}{4^{n}}$

查看试题解析
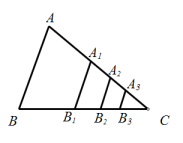12. 如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4直线l经过点B，AE⊥l于点E，CF⊥l于点F，则AE+CF的最大值为（）

A、 $\sqrt{15} + \sqrt{6}$ B、5 C、 $2 \sqrt{6} + \sqrt{2}$ D、 $\sqrt{73}$

查看试题解析

二、填空题

13. 最简二次根式 $\sqrt{3 a - 4}$ 与 $\sqrt{2}$ 是同类二次根式，则 $a$ 的值是.

查看试题解析
14. 如图，将一张矩形纸片沿 $E F$ 折叠，得到两个全等的小矩形 $A B C D$ .如果矩形 $A B C D ∽$ 矩形 $A D F E$ ，那么 $\frac{A B}{A D}$ 的值是.

查看试题解析
15. 已知关于 $x$ 的一元二次方程 $a x^{2} + x + c = 0$ 的两根为 $- 1$ 、 $2$ ，则方程 $c x^{2} - x + a = 0$ 的两根为.

查看试题解析
16. 一个不透明的口袋中有4个完全相同的小球，球上分别标有数字-2，0，1，4.随机摸出一个小球记作m，然后放回，再随机摸出一个小球记作n，则方程 $m x^{2} - 2 x + n ＝ 0$ 是关于x的一元二次方程且此方程无解的概率为 .

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt{12} - 3 t a n 30 ° + {(π - 4)}^{0} + {(- \frac{1}{2})}^{- 1}$ ；

(2)、解方程： $x (2 x - 5) = 4 x - 10$ .

查看试题解析
18. 为做好疫情防控工作，确保师生生命安全，学校每日都在学生进校前进行体温检测．某学校大门 $A B$ 高6.5米，学生 $D F$ 身高1.5米，当学生准备进入体温检测有效识别区域时，在点D处测得摄像头A的仰角为 $30 °$ ，当学生刚好离开体温检测有效识别区域 $C D$ 段时，在点C处测得摄像头A的仰角为 $60 °$ ，求体温检测有效识别区域 $C D$ 段的长（结果保留根号）

查看试题解析
19. 如图，已知 $△ A B C$ 中， $A B = A C$ ，点D、E分别在边 $B C$ 、 $A C$ 上， $∠ A D E = ∠ B$ ．

(1)、求证： $△ A B D ∼ △ D C E$ ；

(2)、若 $A B = 5$ ， $B C = 6$ ， $B D = 2$ ，求点E到 $B C$ 的距离．

查看试题解析
20. 初三年级“黄金分割项目活动”展示，为了解全体初三年级同学的活动成绩，抽取了部分参加活动的同学的成绩进行统计后，分为“优秀”，“良好”，“一般”，“较差”四个等级，并根据成绩绘制成如图两幅不完整的统计图，请结合统计图中的信息，回答下列问题：

(1)、扇形统计图中“优秀”所对应扇形的圆心角为 ▲ 度，并将条形统计图补充完整.

(2)、如果学校初三年级共有340名学生，则参加“黄金分割项目活动”比赛成绩良好的学生有人.

(3)、此次活动中有四名同学获得满分，分别是甲，乙，丙，丁，现从这四名同学中挑选两名同学参加校外举行的“黄金分割项目活动”展示，请用列表法或画树状图法，求出选中的两名同学恰好是甲、丁的概率.

查看试题解析
21. “人与自然和谐共生”哈尔滨湿地节系列活动中，某景点接待游客逐渐增多，6月份第一周接待游客200人，第三周接待游客288人，若该景点接待游客数量的周平均增长率相同.

(1)、求该景点在6月份的第二周接待游客多少人？

(2)、该景点第四周接待游客数量是第二周接待游客数量的1.8倍，平均每位游客购买1件旅游纪念品.该景点只销售A，B两种旅游纪念品，A种纪念品每件利润5元，B种纪念品每件利润8元，且售出的B种纪念品的数量不多于A种纪念品的3倍，设第四周该景点售出A种旅游纪念品a件，获得的总利润为W元，求W与a的函数关系式，并求出获得的最大利润.

查看试题解析
22. 矩形 $A B C D$ 中， $A C$ 、 $B D$ 为对角线， $A B = 4 c m$ ， $B C = 6 c m$ ， $E$ 为 $D C$ 中点，动点 $P$ 从点 $A$ 出发沿 $A B$ 向点 $B$ 运动，动点 $Q$ 同时以相同速度从点 $B$ 出发沿 $B C$ 向点 $C$ 运动， $P$ 、 $Q$ 的速度都是 $1 c m /$ 秒，其中一个动点到达终点时，另一个动点也随之停止运动，设运动时间为 $t$ 秒.

(1)、当 $P Q ∥ A C$ 时，求运动时间 $t$ ；

(2)、当 $P Q ⊥ B D$ 时，求运动时间 $t$ ；

(3)、当 $△ B P Q ∽ △ C E Q$ 时，求运动时间 $t$ ；

(4)、连接 $P E$ ， $△ P Q E$ 的面积能否达到矩形 $A B C D$ 面积的三分之一？若能，求出 $t$ 的值；若不能，说明理由.

查看试题解析