四川省内江市2022-2023学年八年级上学期期末数学试题

试卷更新日期：2023-02-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中运算正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $- \sqrt[3]{27} = - 3$ C、 $\sqrt{49} = \pm 7$ D、 $\sqrt[3]{{(- 8)}^{3}} = 8$

查看试题解析
2. 在实数 $- 1.13$ ， $- π^{2}$ ， 0， $\sqrt[3]{9}$ ， 2.10010001， $\sqrt{8}$ 中，是无理数的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图，点E、F在 $B C$ 上， $A B = C D$ ， $A F = D E$ ， $A F 、 D E$ 相交于点G，添加下列哪一个条件，可使得 $△ A B F ≌ △ D C E$ （）

A、 $∠ B = ∠ C$ B、 $A G = D G$ C、 $∠ A F E = ∠ D E F$ D、 $B E = C F$

查看试题解析
4. 已知 $△ A B C$ 的三条边分别为a，b，c，下列条件不能判断是直角三角形的是（）

A、 $a^{2} = b^{2} - c^{2}$ B、 $a = 6$ ， $b = 8$ ， $c = 10$ C、 $∠ A = ∠ B + ∠ C$ D、 $∠ A ： ∠ B ： ∠ C = 5 ： 12 ： 13$

查看试题解析
5. 下列运算正确的是（）

A、 ${(- a^{2})}^{3} = - a^{5}$ B、 $a^{3} \cdot a^{5} = a^{15}$ C、 ${(- a^{2} b^{3})}^{2} = a^{4} b^{6}$ D、 $3 a^{2} - 2 a^{2} = a$

查看试题解析
6. 某渔民为估计池塘里鱼的总数，先随机打捞20条鱼给它们分别作上标志，然后放回，待有标志的鱼完全混合于鱼群后，第二次打捞80条，发现其中2条鱼有标志，从而估计该池塘有鱼（）

A、1000条 B、800条 C、600条 D、400条

查看试题解析
7. 已知 $4^{x} = 18 ， 8^{y} = 3$ ，则 $5^{2 x - 6 y}$ 的值为（）

A、5 B、10 C、25 D、50

查看试题解析
8. 如图， $A B / / D C$ ，以点 $A$ 为圆心，小于 $A C$ 的长为半径作圆弧，分别交 $A B$ ， $A C$ 于 $E$ ， $F$ 两点，再分别以 $E$ ， $F$ 为圆心，以大于 $\frac{1}{2} E F$ 长为半径作圆弧两条弧交于点 $G$ ，作射线 $A G$ 交 $C D$ 于点 $H$ ，若 $∠ C = 12 0^{°}$ ，则 $∠ A H D =$ （）

A、 $12 0^{°}$ B、 $3 0^{°}$ C、 $15 0^{°}$ D、 $6 0^{°}$

查看试题解析
9. 为加强疫情防控，云南某中学在校门口区域进行人校体温检测．如图，人校学生要求沿着直线AB单向单排通过校门口，测温仪C与直线AB的距离为3m，已知测温仪的有效测温距离为5m，则学生沿直线AB行走时测温的区域长度为（）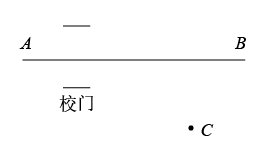

A、4m B、5m C、6m D、8m

查看试题解析
10. 已知 $d = x^{4} - 2 x^{3} + x^{2} - 12 x - 5$ ，则当 $x^{2} - 2 x - 5 = 0$ ， $d$ 的值为（）

A、25 B、20 C、15 D、10

查看试题解析
11. 如图，在△ABC和△ADE中，∠CAB＝∠DAE＝36°，AB＝AC，AD＝AE.连接CD，连接BE并延长交AC，AD于点F，G.若BE恰好平分∠ABC，则下列结论错误的是（）

A、∠ADC＝∠AEB B、 $C D ∥ A B$ C、DE＝GE D、CD＝BE

查看试题解析
12. 已知Rt $△$ ABC中，∠ACB＝90°，AC＝BC，AB＝4 $\sqrt{2}$ ，D为BC的中点，E是线段AB上一点，连接CE、DE，则CE+DE的最小值是（）

A、2 $\sqrt{3}$ B、2 $\sqrt{5}$ C、4 $\sqrt{2}$ D、2+2 $\sqrt{2}$

查看试题解析

二、填空题

13. 分解因式： $- a^{2} + 4 b^{2} =$ .

查看试题解析
14. 已知关于 $x$ 的二次三项式 $x^{2} + 2 k x + 16$ 是完全平方式，则实数k的值为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ 1 = 40 °$ ， $∠ 2 = ∠ 3$ ，则 $∠ C D E =$ 度.

查看试题解析
16. 我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式 $A = a^{2} + a$ ，请结合你所学知识，判断下列说法：①当 $a = - 2$ 时， $A = 2$ ；②无论a取任何实数，不等式 $A + \frac{1}{4} \geq 0$ 恒成立；③若 $A - 1 = 0$ ，则 $a^{2} + \frac{1}{a^{2}} = 4$ ；正确的有.

查看试题解析

三、解答题

17.

(1)、计算： $- 1^{2022} \div \frac{1}{4} + 2^{- 2} \times \sqrt[3]{- 64}$ ；

(2)、先化简，再求值： ${(a + 1)}^{2} - (a + 3) (a - 3) + (a^{4} - 2 a^{3}) \div a^{2}$ ，其中 $a = - 2$ .

查看试题解析
18. 如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ ， $A D$ 也是 $B C$ 边上的中线.
求证： $A B = A C$ .

查看试题解析
19. 为落实“双减”政策，某校利用课后服务开展了“书香校园”的读书活动，活动中，为了解学生对书籍种类（A：艺术类，B：科技类，C：文学类，D：体育类）的喜欢情况，在全校范围内随机抽取若干名学生，进行问卷调查（每个被调查的学生必须选择而且只能在这四种类型中选择一项）将数据进行整理并绘制成两幅不完整的统计图.

(1)、这次调查中，一共调查了名学生；

(2)、在扇形统计图中，求“B”部分所对应的圆心角的度数，并补全条形统计图；

(3)、若全校有2400名学生，请估计喜欢D类的学生有多少名？

查看试题解析
20. 随着疫情的持续，各地政府储存了充足的防疫物品.某防疫物品储藏室的截面是由如图所示的图形构成的，图形下面是长方形ABCD，上面是半圆形，其中 $A B = 2.3 m$ ， $B C = 2.6 m$ ，一辆装满货物的运输车，其外形高2.6m，宽2.4m，它能通过储藏室的门吗？请说明理由.

查看试题解析
21. 我们将 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 进行变形，如： $a^{2} + b^{2} = {(a + b)}^{2} - 2 a b$ ， $a b = \frac{{(a + b)}^{2} - (a^{2} + b^{2})}{2}$ 等.根据以上变形解决下列问题：

(1)、已知 $a^{2} + b^{2} = 12$ ， ${(a + b)}^{2} = 20$ ，则 $a b =$ ；

(2)、若x满足 ${(2022 - x)}^{2} + {(x - 2019)}^{2} = 2020$ ，求 $(2022 - x) (x - 2019)$ 的值；

(3)、如图，在长方形 $A B C D$ 中， $A B = 10$ ， $B C = 6$ ，点E、F分别是 $B C$ 、 $C D$ 上的点，且 $B E = D F = x$ ，分别以 $F C$ 、 $C E$ 为边在长方形 $A B C D$ 外侧作正方形 $C F G H$ 和 $C E M N$ ，若长方形 $C E P F$ 的面积为40，求图中阴影部分的面积和.

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ， D是BC边上的一个动点（其中 $0 ° < ∠ B A D < 45 °$ ），以AD为直角边作 $R t △ A D E$ ，其中 $∠ D A E = 90 °$ ，且 $A D = A E$ ， DE交AC于点F，过点A作 $A G ⊥ D E$ 于点G并延长交BC于点H.

(1)、求证： $△ A B D ≌ △ A C E$ ；

(2)、探索BD、CH、DH的数量关系，并说明理由；

(3)、求证：当 $∠ B A D = 22.5 °$ 时， $S_{△ A D G} = (\sqrt{2} + 1) S_{△ A G F}$ .

查看试题解析