四川省达州市通川区2022-2023学年七年级上学期期末数学试题

试卷更新日期：2023-02-16 类型：期末考试

进入出卷网下载

一、单选题

1. 目前，成都市已累计改造的老旧小区惠及居民约45万户，大力促进了人居环境有机更新，提升了市民幸福指数．将数据45万用科学记数法表示为（）

A、4.5×10⁵ B、4.5×10⁴ C、45×10⁴ D、0.45×10⁶

查看试题解析
2. 《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数，一批零件超过规定长度记为正数，短于规定长度记为负数，越接近规定长度质量越好.检查其中四个，结果如下：第一个为0.05mm，第二个为-0.02mm，第三个为-0.04mm，第四个为0.03mm，则这四个零件中质量最好的是（）

A、第一个 B、第二个 C、第三个 D、第四个

查看试题解析
3. 下面调查中，最适合采用全面调查的是（）

A、对全国中学生视力状况的调查 B、了解莲花湖的鱼的重量 C、对“天舟三号”货运飞船零部件的调查 D、调查人们垃圾分类的意识

查看试题解析
4. 下列计算正确的是（）

A、 $2 x + 3 y = 5 x y$ B、 $3 x^{2} + 2 x^{2} = 5 x^{4}$ C、 $- 2 (x - 2 y) = - 2 x - 2 y$ D、 $- x^{2} y + 2 x^{2} y = x^{2} y$

查看试题解析
5. 下列图形经过折叠能围成一个正方体的是（）

A、 B、 C、 D、

查看试题解析
6. 下列说法中，错误的是（）

A、顶点在圆心的角叫做圆心角 B、 $540 0^{″}$ 等于 $1.5 °$ C、各边相等的多边形叫做正多边形 D、在数轴上，与表示-1的点的距离为3的数有2和-4.

查看试题解析
7. 元代名著《算学启蒙》中有一题：驽马日行一百五十里，良马日行二百四十里.驽马先行一十二日，问良马几何追及之.译文是：跑得慢的马每天走150里，跑得快的马每天走240里.慢马先走12天，问快马需要几天可追上慢马？若设快马需要x天可追上慢马，则由题意，可列方程为（）

A、150×12+x＝240x B、150（12+x）＝240x C、150x＝240（x-12） D、150x＝240（x+12）

查看试题解析
8. 如图，数轴上点M，P，N分别表示数m，m+n，n，那么原点的位置是（）

A、在线段MP上 B、在线段PN上 C、在点M的左侧 D、在点N的右侧

查看试题解析

二、填空题

9. 若 $| x - 2 | + {(y + 3)}^{2} = 0$ ，则 ${(x + y)}^{2023} =$ .

查看试题解析
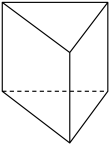
10. 如图，用一个平面去截一个三棱柱，截面的形状可能是.
①三角形②四边形③五边形④六边形

查看试题解析
11. 若关于x的方程 $(3 a + 2) x^{2} + 4 x^{k - 1} - 5 = 0$ 是一元一次方程，则关于x的方程 $a x + k = 0$ 的解是.

查看试题解析
12. 如图，两块直角三角板的直角顶点O重合在一起，若 $∠ B O C = \frac{1}{7} ∠ A O D$ ，则∠BOC的度数为.

查看试题解析
13. 如图，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第6个图形需要黑色棋子的个数是，第 $n$ 个图形需要的黑色棋子的个数是．（ $n$ 为正整数）

查看试题解析
14. 已知a，b，c三个有理数在数轴上对应的位置如图所示，化简|c-a|-|a-b|-|b|＝.

查看试题解析
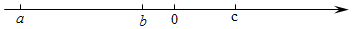15. 过某个多边形一个顶点的所有对角线，将这个多边形分成5个三角形，则这个多边形是边形.

查看试题解析
16. 规定如下两种运算：x⊗y＝2xy+1；x⊕y＝x+2y-1.例如：2⊗3＝2×2×3+1＝13；2⊕3＝2+2×3-1＝7.若a⊗（4⊕5）的值为79，则3a+2[3a-2（2a-1）]的值是 .

查看试题解析
17. 如图，点 $C$ 是线段 $A B$ 上一点， $A C > B C$ ，点 $M$ 是线段 $A B$ 的中点，点 $N$ 是线段 $B C$ 的中点， $A M = 8$ ， $C N = 3$ ，则线段 $M N$ 的长度为.

查看试题解析
18. 如图所示，将形状大小完全相同的“ $▱$ ”按照一定规律摆成下列图形，第1幅图中“ $▱$ ”的个数为 $a_{1}$ ，第2幅图中“ $▱$ ”的个数为 $a_{2}$ ，第3幅图中“ $▱$ ”的个数为 $a_{3}$ …，以此类推， $\frac{2}{a_{1}} + \frac{2}{a_{2}} + \frac{2}{a_{3}} + \frac{2}{a_{4}} + \cdot \cdot \cdot \cdot \cdot \cdot + \frac{2}{a_{2022}}$ 的值为.

查看试题解析

三、解答题

19.

(1)、计算： $40 + (\frac{1}{6} - \frac{2}{3} + \frac{3}{4}) \times 12$ ；

(2)、计算： $| - 1^{4} | - (1 - 0.5) \times (- 1 \frac{1}{3}) \times [3 - (- 3)^{2}]$ .

查看试题解析
20. 解方程： $\frac{2 x - 7}{3} = \frac{2 - 3 x}{2} + 1$

查看试题解析
21. 先化简，再求值： $a^{2} b + (3 a^{2} b + a b^{2}) - 2 (2 a b^{2} + a^{2} b)$ ，其中 $a = 2$ ， $b = - 3$ .

查看试题解析
22. 为了解同学们更喜欢什么球类运动，以便学校组织受同学们欢迎的比赛，学生会体育部的部长小强随机调查了部分同学对五种球类运动（A：篮球、B：足球、C：排球、D：乒乓球、E：羽毛球）的喜欢程度，并将结果绘制成如下两幅不完整的统计图.

(1)、此次共调查了名学生；

(2)、扇形统计图中，D：乒乓球所对应的扇形圆心角的大小为度；

(3)、通过计算补全条形统计图；

(4)、学校共有980名学生，估计该校学生喜欢篮球的有多少人？

查看试题解析
23. 如图， $∠ A O B = 90 °$ ， $∠ A O C = 60 °$ ， ON平分 $∠ A O C$ ， OM平分 $∠ B O C$ ，

(1)、求 $∠ M O N$ 的度数？

(2)、若 $∠ A O C = 40 °$ ，其他条件不变， $∠ M O N =$ ；若 $∠ A O B = 100 °$ ，其他条件不变， $∠ M O N =$ ；如果 $∠ A O B = α$ ， $∠ A O C = β$ （ $α > β$ ）其他条件不变，那么 $∠ M O N =$ .

查看试题解析
24. （概念学习）规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如 $2 \div 2 \div 2$ ， $(- 3) ÷ (- 3) ÷ (- 3) ÷ (- 3)$ 等.类比有理数的乘方，我们把 $2 \div 2 \div 2$ 记作 $2^{③}$ ，读作“2的圈3次方”， $(- 3) ÷ (- 3) ÷ (- 3) ÷ (- 3)$ 记作 ${(- 3)}^{④}$ ，读作“ $- 3$ 的圈4次方”，一般地，把 $\underset{n 个}{\underset{︸}{a \div a \div a \div \cdot \cdot \cdot \div a}} (a \neq 0)$ 记作，读作“a的圈n次方”.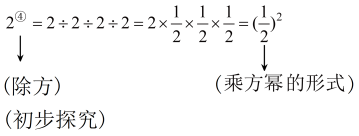

(1)、直接写出计算结果： $5^{③} =$ ， ${(- \frac{1}{3})}^{④} =$ .

(2)、（深入思考）我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘法运算此处不用作答）
试一试：仿照上面的算式，将下列运算结果直接写成幂的形式 ${(- 3)}^{⑤} =$ ； ${(\frac{1}{2})}^{⑩} =$ .

(3)、算一算： $- 9^{2} \div {(- \frac{1}{3})}^{⑤} \times {(- \frac{1}{4})}^{④} - {(- \frac{1}{5})}^{4} \div 5^{④}$ .

查看试题解析
25. 2021年国庆期间，某景区对门票采用灵活的售票方法吸引游客，按团队人数分段定价售票，信息如表：
团队人数（人）
小于10人
10人及以上且小于30人
30人及以上
门票单价
60元
50元
40元
注：本题中的门票款不含导游的门票.

(1)、导游小张于10月1日带了一个30人的旅游团到该景区，请问需要支付多少元门票款？

(2)、导游小李于10月1日带A团，10月2日带B团都到该景区旅游，共付门票款1800元，A，B两个团队合计42人，A团人数比B团人数少，求A，B两个团队各有多少人？

查看试题解析
26. 如图，数轴上点M，N对应的实数分别为-6和8，数轴上一条线段AB从点M出发（刚开始点A与点M重合），以每秒1个单位的速度沿数轴在M，N之间往返运动（点B到达点N立刻返回），线段AB＝2，设线段AB的运动时间为t秒.

(1)、如图1，当t＝2时，求出点A对应的有理数和点B与点N之间的距离；

(2)、如图2，当线段AB从点M出发时，在数轴上的线段CD从点N出发（D在C点的右侧，刚开始点D与点N重合），以每秒2个单位的速度沿数轴在N，M之间往返运动（点C到达点M立刻返回），CD＝4，点P为线段AB的中点，点Q为线段CD的中点.
①当P点第一次到达原点O之前，若点P、点Q到数轴原点的距离恰好相等，求t的值；
②我们把数轴上的整数对应的点称为“整点”，当P，Q两点第一次在整点处重合时，请求出此时点C对应的数.

查看试题解析

团队人数（人）	小于10人	10人及以上且小于30人	30人及以上
门票单价	60元	50元	40元