四川省达州市通川区2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-02-16 类型:期末考试
一、单选题
-
1. 把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列事件为必然事件的是( )
2. 下列事件为必然事件的是( )
A、任意买一张电影票,座位号是偶数 B、打开电视机,正在播放动画片 C、3个人分成两组,一定有2个人分在一组 D、三根长度为2cm,2cm,4cm的木棒能摆成三角形3. 在中, , , 则的值为( )A、 B、 C、 D、4. 如图,EF是一个杠杆,可绕支点O自由转动,若动力和阻力的施力方向都始终保持竖直向下,当阻力不变时,则杠杆向下运动时的大小变化情况是( )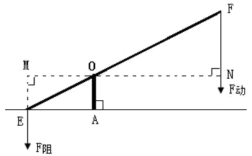 A、越来越小 B、不变 C、越来越大 D、无法确定5. 若是关于x的一元二次方程的一个根,则k的值为( )A、-1 B、0 C、1 D、26. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( )
A、越来越小 B、不变 C、越来越大 D、无法确定5. 若是关于x的一元二次方程的一个根,则k的值为( )A、-1 B、0 C、1 D、26. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( )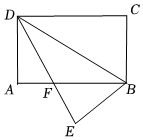 A、 B、 C、 D、7. 如图,已知.
A、 B、 C、 D、7. 如图,已知.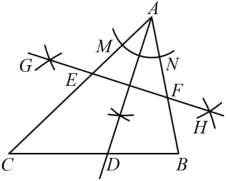 (1)、以点为圆心,以适当长为半径画弧,交于点 , 交于点.(2)分别以M,N为圆心,以大于的长为半径画弧,两弧在的内部相交于点.(3)作射线交于点D.(4)分别以A,D为圆心,以大于的长为半径画弧,两弧相交于G,H两点.(5)作直线 , 交分别于点E,F.
(1)、以点为圆心,以适当长为半径画弧,交于点 , 交于点.(2)分别以M,N为圆心,以大于的长为半径画弧,两弧在的内部相交于点.(3)作射线交于点D.(4)分别以A,D为圆心,以大于的长为半径画弧,两弧相交于G,H两点.(5)作直线 , 交分别于点E,F.依据以上作图,若 , , , 则的长是( ).
A、2 B、1 C、 D、48. 在平面直角坐标系中,已知点 , .若与关于点位似,且 , 则点的坐标为( )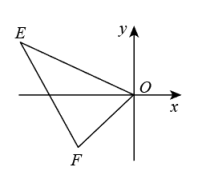 A、 B、 C、或 D、或9. 如图,在直角坐标系中,以坐标原点 , , 为顶点的 , 其两个锐角对应的外角角平分线相交于点 , 且点恰好在反比例函数的图象上,则的值为( )
A、 B、 C、或 D、或9. 如图,在直角坐标系中,以坐标原点 , , 为顶点的 , 其两个锐角对应的外角角平分线相交于点 , 且点恰好在反比例函数的图象上,则的值为( )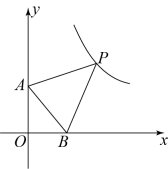 A、36 B、25 C、16 D、910. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:
A、36 B、25 C、16 D、910. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:① ;② ;③ ;④ ;⑤ .
其中正确的是( )
 A、①②③ B、①③④ C、①④⑤ D、②③④
A、①②③ B、①③④ C、①④⑤ D、②③④二、填空题
-
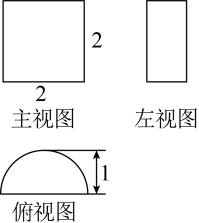
11. 我们把宽与长的比是 的矩形叫做黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形ABCD是黄金矩形,边AB的长度为 1,则该矩形的周长为 .12. 一个几何体的三视图如图所示,则该几何体的体积为 .
 13. 如图,正比例函数 , 一次函数和反比例函数的图象在同一直角坐标系中,若 , 则自变量的取值范围是.
13. 如图,正比例函数 , 一次函数和反比例函数的图象在同一直角坐标系中,若 , 则自变量的取值范围是.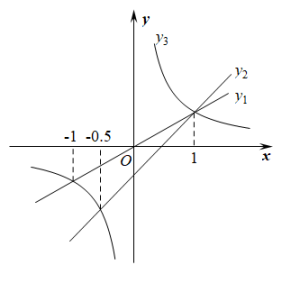 14. 在正方形网格中,的位置如图所示,则的值为.
14. 在正方形网格中,的位置如图所示,则的值为.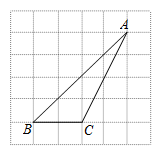 15. 如图1,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图2的图案,记阴影部分的面积为 ,空白部分的面积为 ,大正方形的边长为 ,小正方形的边长为 ,若 ,则 的值为.
15. 如图1,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图2的图案,记阴影部分的面积为 ,空白部分的面积为 ,大正方形的边长为 ,小正方形的边长为 ,若 ,则 的值为.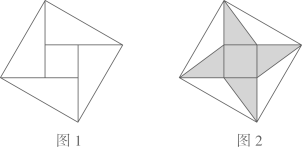
三、解答题
-
16. 计算:17. 如图,在平面直角坐标系中,△ABC和关于点E成中心对称,
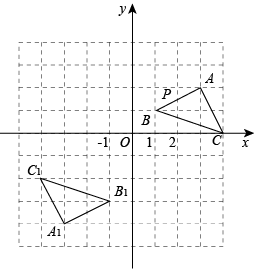
⑴在图中标出点E,且点E的坐标为 ▲ ;
⑵点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点的坐标为(a-6,b+2),请画出上述平移后的 , 此时的坐标为 ▲ , 的坐标为 ▲ ;
⑶若和关于点F成位似三角形,则点F的坐标为 ▲ .18. 为了解全校1000名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.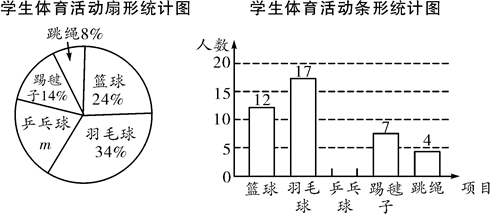 (1)、m= ▲ , 这次共抽取了 ▲ 名学生进行调查;并补全条形图;(2)、请你估计该校约有多少名学生喜爱打篮球;(3)、现学校准备从喜欢跳绳活动的4人(三女一男)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?19. 如图,已知在菱形中,对角线与交于点 , 延长到点 , 使 , 延长到点 , 使 , 顺次连接点 , 若 , .
(1)、m= ▲ , 这次共抽取了 ▲ 名学生进行调查;并补全条形图;(2)、请你估计该校约有多少名学生喜爱打篮球;(3)、现学校准备从喜欢跳绳活动的4人(三女一男)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?19. 如图,已知在菱形中,对角线与交于点 , 延长到点 , 使 , 延长到点 , 使 , 顺次连接点 , 若 , .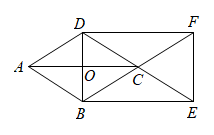 (1)、求证:四边形是矩形;(2)、求四边形的周长为多少.20. 如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌.小明在山坡的坡脚A处测得宣传牌底部D的仰角为 , 沿山坡向上走到B处测得宣传牌顶部C的仰角为.已知山坡的坡度米,米.
(1)、求证:四边形是矩形;(2)、求四边形的周长为多少.20. 如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌.小明在山坡的坡脚A处测得宣传牌底部D的仰角为 , 沿山坡向上走到B处测得宣传牌顶部C的仰角为.已知山坡的坡度米,米.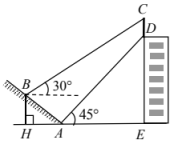 (1)、;点B距水平面的高度米;(2)、求广告牌的高度.(结果精确到0.1米,参考数据:.)21. 2022成都世乒赛期间,某店直接从工厂购进A、B两款纪念品,进货价和销售价如下表:(注:利润销售价进货价)
(1)、;点B距水平面的高度米;(2)、求广告牌的高度.(结果精确到0.1米,参考数据:.)21. 2022成都世乒赛期间,某店直接从工厂购进A、B两款纪念品,进货价和销售价如下表:(注:利润销售价进货价)类别价格
A款纪念品
B款纪念品
进货价(元/件)
20
15
销售价(元/件)
35
27
(1)、该店第一次用850元购进A、B款纪念品共50件,求两款纪念品分别购进的件数;(2)、第一次购进的纪念品售完后,该网店计划再次购进A、B两款纪念品共200件(进货价和销售价都不变),且进货总价不高于3200元,应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?(3)、成都世乒赛临近结束时,网店打算把B款纪念品调价销售.如果按照原价销售,平均每天可售4件,经调查发现,每降价1元,平均每天可多售2件,将销售价定为每件多少元时,才能使B款纪念品平均每天销售利润为90元?22. 如图,已知一次函数与反比例函数的图象在第一、三象限分别交于 , 两点,连接.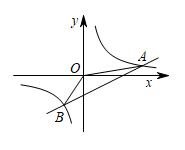 (1)、求一次函数和反比例函数的解析式;(2)、轴上是否存在一点 , 能使 , 若存在,请求出的坐标;若不存在,请说明理由.23. 如图,四边形ABCD是正方形,点P是线段AB的延长线上一点,点M是线段AB上一点,连接DM,以点M为直角顶点作MN⊥DM交∠CBP的角平分线于N,过点C作CEMN交AD于E,连接EM,CN,DN.
(1)、求一次函数和反比例函数的解析式;(2)、轴上是否存在一点 , 能使 , 若存在,请求出的坐标;若不存在,请说明理由.23. 如图,四边形ABCD是正方形,点P是线段AB的延长线上一点,点M是线段AB上一点,连接DM,以点M为直角顶点作MN⊥DM交∠CBP的角平分线于N,过点C作CEMN交AD于E,连接EM,CN,DN.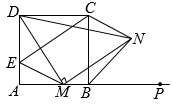 (1)、求证:DM=MN;(2)、求证:EMCN.24. 阅读理解:
(1)、求证:DM=MN;(2)、求证:EMCN.24. 阅读理解:材料一:若三个非零实数x,y,z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x,y,z构成“和谐三数组”.
材料二:若关于x的一元二次方程ax2+bx +c= 0(a≠0)的两根分别为 , ,则有 , .
问题解决:
(1)、请你写出三个能构成“和谐三数组”的实数;(2)、若 , 是关于x的方程ax2+bx +c= 0 (a,b,c均不为0)的两根, 是关于x的方程bx+c=0(b,c均不为0)的解.求证:x1 , x2 , x3可以构成“和谐三数组”;(3)、若A(m,y1) ,B(m + 1,y2) ,C(m+3,y3)三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成“和谐三数组”,求实数m的值.25.(1)、【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.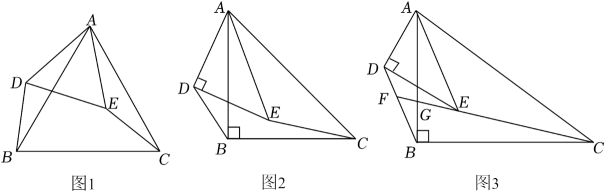 (2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.
(2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.①求的值;
②延长CE交BD于点F,交AB于点G.求sin∠BFC的值.