四川省达州市开江县2022-2023学年八年级上学期期末数学试题

试卷更新日期：2023-02-16 类型：期末考试

进入出卷网下载

一、单选题

1. △ABC的三条边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是（）

A、a²＋b²＝c² B、∠A＝∠B＋∠C C、∠A∶∠B∶∠C＝3∶4∶5 D、a＝5，b＝12，c＝13

查看试题解析
2. 下列语句正确的是（）

A、4是16的算术平方根，即± $\sqrt{16}$ ＝4 B、-3是27的立方根 C、 $\sqrt{64}$ 的立方根是2 D、1的立方根是-1

查看试题解析
3. 已知点 $A (\sqrt{2} ， 5)$ ，则点A关于x轴对称的点 $A^{'}$ 的坐标是（）

A、 $(- 5 ， - \sqrt{2})$ B、 $(- \sqrt{2} ， 5)$ C、 $(- \sqrt{2} ， - 5)$ D、 $(\sqrt{2} ， - 5)$

查看试题解析

4. 甲、乙、丙、丁四位选手各进行了10次射击，射击成绩的平均数和方差如表：

选手	甲	乙	丙	丁
平均数（环）	9.0	9.0	9.0	9.0
方差	0.25	1.00	2.50	3.00

则成绩发挥最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

5. 函数 $y = k x + b$ 与 $y = b x + k$ 的图象在同一直角坐标系内的大致位置是（）

A、 B、 C、 D、

查看试题解析
6. 在（﹣ $\sqrt{2}$ ）⁰ ， $\sqrt[3]{8}$ ，0， $\sqrt{9}$ ， $\sqrt[3]{4}$ ，0.010010001…， $\frac{π}{2}$ ，﹣0.333…， $\sqrt{5}$ 中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 将一副三角板如图1放置，使点A落在DE上，三角板ABC的顶点C与三角板CDE的直角顶点C重合，若 $B C ∥ D E$ ， AB与CE交于点F，则 $∠ A F C$ 的度数为（）

A、30° B、45° C、60° D、75°

查看试题解析
8. 已知直线 $l_{1} ： y = - x + b$ 与直线 $l_{2} ： y = - k x + 1$ 在同一平面直角坐标系中交于点 $(1 ， - 2)$ ，那么关于x，y的方程组 ${\begin{array}{l} x + y = b \\ k x + y = 1 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$

查看试题解析
9. 甲、乙两人分别从A、B两地同时出发，相向而行，匀速前往B地、A地，两人相遇时停留了4min，又各自按原速前往目的地.甲、乙两人之间的距离y（m）与甲所用时间x（min）之间的函数关系如图所示，有下列说法：①A、B之间的距离为2400m；②甲、乙行走的速度比是 $2 ： 3$ ；③ $a = 800$ ；④ $b = 34$ .其中正确结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在直角坐标系中，直角三角形ABC的顶点A在x轴上，顶点B在y轴上， $∠ A C B = 9 0^{°}$ ，点C的坐标为 $(1 ， 2)$ ，点D和点C关于 $A B$ 成轴对称，且AD交y轴于点E.那么点E的坐标为（）

A、 $(0 ， \frac{5}{4})$ B、 $(0 ， \frac{3}{4})$ C、 $(0 ， \frac{6}{5})$ D、 $(0 ， \frac{4}{5})$

查看试题解析

二、填空题

11. 已知 $x$ 、 $y$ ，满足 $\sqrt{x - 1} + | y + 2 | = 0$ ，则 $x^{2} - 4 y$ 的平方根为．

查看试题解析
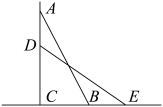
12. 已知方程组 ${\begin{array}{l} 5 x + y = 3 \\ m x + 5 y = 4 \end{array}$ 与 ${\begin{array}{l} x - 2 y = 5 \\ 5 x + n y = 1 \end{array}$ 有相同的解，则 $2 m - n =$ .

查看试题解析
13. 如图，一架梯子AB长5米，底端离墙的距离BC为3米，当梯子下滑到DE时， $A D = 1$ 米，则BE＝米.

查看试题解析
14. 如图，已知AB//CD//EF，则∠1＝60°，∠3＝20°，则∠2＝.

查看试题解析
15. 如图，点 $A_{1} (2 ， 2)$ 在直线 $y = x$ 上，过点作 $A_{1} B_{1} // y$ 轴交直线 $y = \frac{1}{2} x$ 于点 $B_{1}$ ，以点 $A_{1}$ 为直角顶点， $A_{1} B_{1}$ 为直角边在 $A_{1} B_{1}$ 的右侧作等腰直角 $△ A_{1} B_{1} C_{1}$ ，再过 $C_{1}$ 点作过点 $A_{2} B_{2} // y$ 轴交直线 $y = x$ 和直线 $y = \frac{1}{2} x$ 于 $A_{2}$ ， $B_{2}$ 两点，以点 $A_{2}$ 为直角顶点， $A_{2} B_{2}$ 为直角边在 $A_{2} B_{2}$ 的右侧作等腰直角 $△ A_{2} B_{2} C_{2}$ ，…，按此规律进行下去，则等腰直角 $△ A_{n} B_{n} C_{n}$ 的边长 $B_{n} C_{n}$ 为.（用含正整数n的代数式表示）

查看试题解析

三、解答题

16. 解答题

(1)、计算： $\sqrt{12} - 3 \sqrt{\frac{1}{3}} + | \sqrt{3} - 2 |$ ；

(2)、解方程组： ${\begin{array}{l} 3 x - y = 7 \\ x + 3 y = - 1 \end{array}$ .

查看试题解析
17. 在学校组织的“最美数学小报”的评比中，校团委给每个同学的作品打分，成绩分为 $A ， B ， C ， D$ 四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，将八（1）班与八（2）班的成绩整理并绘制成如下统计图：

请你根据以上提供的信息解答下列问题：

(1)、将表格补充完整.

平均数（分）
中位数（分）
众数（分）
八（1）班
83.75
80
八（2）班
80

(2)、若八（1）班有40人，且评分为B级及以上的同学有纪念奖章，请问该班共有几位同学得到奖章？

查看试题解析
18. 如图，平面直角坐标系中， $△ A B C$ 的顶点都在网格点上，其中 $A (- 4 ， 5)$ ， $B (- 2 ， 1)$ ， $A (- 1 ， 3)$ .

(1)、作出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、求 $△ A B C$ 的面积；

(3)、在x轴上是否存在一点P，使 $P A + P B$ 的和最短？如果存在，请求出此时 $P A + P B$ 的值；如果不存在，请说明理由.

查看试题解析
19. 拖拉机行驶过程中会对周围产生较大的噪声影响．如图，有一台拖拉机沿公路AB由点A向点B行驶，已知点C为一所学校，且点C与直线AB上两点A，B的距离分别为150m和200m，又AB＝250m，拖拉机周围130m以内为受噪声影响区域．

(1)、学校C会受噪声影响吗？为什么？

(2)、若拖拉机的行驶速度为每分钟50米，拖拉机噪声影响该学校持续的时间有多少分钟？

查看试题解析
20. 已知平面直角坐标系中一点P(m+1，2m-4)，根据下列条件，求点P的坐标.

(1)、若点Q(-3，2)，且直线PQ与y轴平行；

(2)、若点P到x轴，y轴的距离相等.

查看试题解析
21. 为了做好防疫工作，学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元，5瓶A型消毒液和4瓶B型消毒液共需71元.

(1)、这两种消毒液的单价各是多少元？

(2)、学校准备购进这两种消毒液共90瓶，且A型消毒液的数量不超过67瓶，请设计出最省钱的购买方案，并求出最少费用.

查看试题解析
22. 如图1， $G$ ， $E$ 是直线 $A B$ 上两点，点 $G$ 在点 $E$ 左侧，过点 $G$ 的直线 $G P$ 与过点 $E$ 的直线 $E P$ 交于点 $P$ .直线 $P E$ 交直线 $C D$ 于点 $H$ ，满足点 $E$ 在线段 $P H$ 上， $∠ P G B = ∠ P H D - ∠ P$ .

(1)、求证： $A B ∥ C D$ ；

(2)、如图2，点 $Q$ 在直线 $A B$ ， $C D$ 之间， $P H$ 平分 $∠ Q H D$ ， $G F$ 平分 $∠ P G B$ ，点 $F$ ， $G$ ， $Q$ 在同一直线上，且 $2 ∠ Q + ∠ P = 120 °$ ，求 $∠ Q H D$ 的度数；

(3)、在（2）的条件下，若点 $M$ 是直线 $P G$ 上一点，直线 $M H$ 交直线 $A B$ 于点 $N$ ，点 $N$ 在点 $B$ 左侧，请直接写出 $∠ M N B$ 和 $∠ P H M$ 的数量关系.（题中所有角都是大于 $0 °$ 且小于 $180 °$ 的角）

查看试题解析
23. 在平面直角坐标系中， $P (a ， b)$ 是第一象限内一点，给出如下定义： $k_{1} = \frac{a}{b}$ 和 $k_{2} = \frac{b}{a}$ 两个值中的最大值叫做点P的“倾斜系数”k.

(1)、求点 $P (6 ， 2)$ 的“倾斜系数”k的值；

(2)、①若点 $P (a ， b)$ 的“倾斜系数” $k = 2$ ，请写出a和b的数量关系，并说明理由；
②若点 $P (a ， b)$ 的“倾斜系数” $k = 2$ ，且 $a + b = 3$ ，求OP的长；

(3)、如图，已知点 $A (2 ， 2)$ ， $B (4 ， 2)$ ， $C (4 ， 4)$ ， $D (2 ， 4)$ ， $P (a ， b)$ 是四边形形ABCD上任意一点.试说明是否存在使点P的“倾斜系数”k为 $\frac{3}{2}$ 的点.若存在，请直接写出这样的点P的坐标；若不存在，请说明理由.

查看试题解析
24. 已知： $△ A B C$ 中， $∠ C A B = 60 °$ ， D是 $B C$ 的中点，延长 $A B$ 到点E，使 $B E = A C$ ，连接 $C E$ ， $A D$ .

(1)、如图1，若 $△ A B C$ 是等边三角形， $A D = 3$ ，则 $C E$ 的长等于；

(2)、如图2，过点B作 $A C$ 的平行线交 $A D$ 的延长线于点F，连接 $E F$ .
①求证： $△ B E F$ 是等边三角形；
②求证： $C E = 2 A D$ .

查看试题解析
25. 如图1，已知函数 $y = \frac{1}{2} x + 3$ 与x轴交于点A，与y轴交于点B，点C与点A关于y轴对称.

(1)、求直线BC的函数解析式；

(2)、设点M是x轴上的一个动点，过点M作y轴的平行线，交直线AB于点P，交直线BC于点Q.
①若△PQB的面积为 $\frac{7}{2}$ ，求点Q的坐标；
②点M在线段AC上，连接BM，如图2，若∠BMP＝∠BAC，直接写出P的坐标.

查看试题解析

	平均数（分）	中位数（分）	众数（分）
八（1）班	83.75	80
八（2）班			80