四川省自贡市富顺县富世学区2021-2022学年九年级下学期第一学月考数学试题
试卷更新日期:2023-02-16 类型:月考试卷
一、单选题
-
1. 2020年12月17日凌晨,嫦娥5号返回器携带月球样本成功着陆!已知地球到月球的平均距离约为380000千米.数据380000用科学记数法表示为( )A、 B、 C、 D、2. 下列各式中,计算正确的是( )A、 B、 C、 D、3. 下列标志中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,内接于圆O,连接、 , , 则的度数是( )
4. 如图,内接于圆O,连接、 , , 则的度数是( ) A、 B、 C、 D、5. 在一个布袋中装有红、白两种颜色的小球,它们除颜色外没有任何其他区别.其中红球若干,白球5个,袋中的球已搅匀.若从袋中随机取出1个球,取出红球的可能性大,则红球的个数是( )A、4个 B、5个 C、不足4个 D、6个或6个以上6. 如果 ,那么x的值为( )A、2或-1 B、0或1 C、2 D、-17. 定理:三角形的一个外角等于与它不相邻的两个内角的和.
A、 B、 C、 D、5. 在一个布袋中装有红、白两种颜色的小球,它们除颜色外没有任何其他区别.其中红球若干,白球5个,袋中的球已搅匀.若从袋中随机取出1个球,取出红球的可能性大,则红球的个数是( )A、4个 B、5个 C、不足4个 D、6个或6个以上6. 如果 ,那么x的值为( )A、2或-1 B、0或1 C、2 D、-17. 定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD是的外角,求证:.
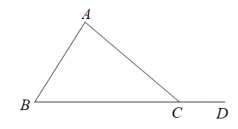
证法1:如图.
∵(三角形内角和定理)
又∵(平角定义)
∴(等量代换)
∴(等式性质)
证法2:如图,
∵ , ,
且(量角器测量所得)
又∵(计算所得)
∴(等量代换)
下列说法正确的是( )
A、证法1还需证明其他形状的三角形,该定理的证明才完整 B、证法1用严谨的推理证明了该定理 C、证法2用特殊到一般法证明了该定理 D、证法2只要测量够一百个三角形进行验证,就能证明该定理8. 如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E,若点E是AD的中点,以点B为圆心,BE长为半径画弧,交BC于点F,则图中阴影部分的面积是( ) A、2- B、- C、2- D、-9. 若一元二次方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 且 D、 且10. 如图,已知点A是双曲线y= 在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
A、2- B、- C、2- D、-9. 若一元二次方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 且 D、 且10. 如图,已知点A是双曲线y= 在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( ) A、n=-2m B、n=- C、n=-4m D、n=-11. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )
A、n=-2m B、n=- C、n=-4m D、n=-11. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )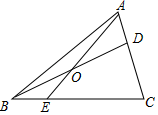 A、1:2 B、1:3 C、1:4 D、2:312. 已知A、B两点的坐标分别为、 , 线段上有一动点 , 过点M作x轴的平行线交抛物线于、两点.若 , 则a的取值范围为( )A、 B、 C、 D、
A、1:2 B、1:3 C、1:4 D、2:312. 已知A、B两点的坐标分别为、 , 线段上有一动点 , 过点M作x轴的平行线交抛物线于、两点.若 , 则a的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 分解因式: =14. 要使分式 有意义,则x的取值范围为 .15. 九班一小组名同学的生物测试成绩依次为: , , , , , , , 这组数据的中位数和众数分别是.16. 已知关于 的方程 ( )的两实数根为 , ,若 ,则 .17. 将一张圆形纸片(圆心为点O)沿直径对折后,按图1分成六等份折叠得到图2,将图2沿虚线剪开,再将展开得到如图3的一个六角星.若 , 则的度数为.
 18. 如图,在平面直角坐标系中,A(2,0)、B(0,2)、C(4,0)、D(3,2),P是AOB外部的第一象限内一动点,且∠BPA=135°,则2PD+PC的最小值是.
18. 如图,在平面直角坐标系中,A(2,0)、B(0,2)、C(4,0)、D(3,2),P是AOB外部的第一象限内一动点,且∠BPA=135°,则2PD+PC的最小值是.
三、解答题
-
19. 计算:20. 如图,一次函数 的图象与 轴、 轴分别交于点 , ,与反比例函数 ( )的图象交于点 , .
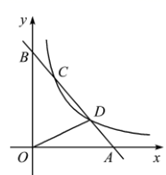 (1)、分别求出两个函数的解析式;(2)、连接 ,求 的面积.21. 今年五、六月份,我省各地、市普遭暴雨袭击,水位猛涨.某市抗洪抢险救援队伍在B处接到报告:有受灾群众被困于一座遭水淹的楼顶A处,情况危急!救援队伍在B处测得A在B的北偏东的方向上(如图所示),队伍决定分成两组:第一组马上下水游向A处救人,同时第二组从陆地往正东方向奔跑米到达C处,再从C处下水游向A处救人,已知A在C的北偏东的方向上,且救援人员在水中游进的速度均为1米/秒.在陆地上奔跑的速度为4米/秒,试问哪组救援队先到A处?请说明理由.(参考数据)
(1)、分别求出两个函数的解析式;(2)、连接 ,求 的面积.21. 今年五、六月份,我省各地、市普遭暴雨袭击,水位猛涨.某市抗洪抢险救援队伍在B处接到报告:有受灾群众被困于一座遭水淹的楼顶A处,情况危急!救援队伍在B处测得A在B的北偏东的方向上(如图所示),队伍决定分成两组:第一组马上下水游向A处救人,同时第二组从陆地往正东方向奔跑米到达C处,再从C处下水游向A处救人,已知A在C的北偏东的方向上,且救援人员在水中游进的速度均为1米/秒.在陆地上奔跑的速度为4米/秒,试问哪组救援队先到A处?请说明理由.(参考数据) 22. 为了积极响应我市“打赢蓝天保卫战”的倡议,秉承“低碳生活,绿色出行”的公益理念,越来越多的居民选择共享单车作为出行的交通工具.2018年1月,某公司向市场新投放共享单车640辆.(1)、若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份新投放共享单车多少辆?(2)、考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A、B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆,假设所进车辆全部售完,为了使利润最大,该商城应如何进货?并求出最大利润值.23. 某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行了1000米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图.
22. 为了积极响应我市“打赢蓝天保卫战”的倡议,秉承“低碳生活,绿色出行”的公益理念,越来越多的居民选择共享单车作为出行的交通工具.2018年1月,某公司向市场新投放共享单车640辆.(1)、若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份新投放共享单车多少辆?(2)、考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A、B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆,假设所进车辆全部售完,为了使利润最大,该商城应如何进货?并求出最大利润值.23. 某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行了1000米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图. (1)、根据给出的信息,补全两幅统计图;(2)、该校九年级有600名男生,请估计成绩未达到良好有多少名?(3)、某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛,预赛分为A、B、C三组进行,选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?24. 阅读以下材料,苏格兰数学家纳皮尔(J.Npler,1550-1617年)是对数的创始人,他发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler.1707-1783年)才发现指数与对数之间的联系.
(1)、根据给出的信息,补全两幅统计图;(2)、该校九年级有600名男生,请估计成绩未达到良好有多少名?(3)、某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛,预赛分为A、B、C三组进行,选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?24. 阅读以下材料,苏格兰数学家纳皮尔(J.Npler,1550-1617年)是对数的创始人,他发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler.1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地.若 ( 且 ),那么x叫做以a为底N的对数,
记作 ,比如指数式 可以转化为对数式 ,对数式 可以转化为指数式 .我们根据对数的定义可得到对数的一个性质:
,理由如下:
设 ,则 .
.由对数的定义得
又
.
根据上述材料,结合你所学的知识,解答下列问题:
(1)、填空:① ;② , ③ ;(2)、求证: ;(3)、拓展运用:计算 .25. 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.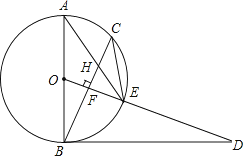 (1)、求证:BD是⊙O的切线;(2)、求证:CE2=EH•EA;(3)、若⊙O的半径为5,sinA= , 求BH的长。
(1)、求证:BD是⊙O的切线;(2)、求证:CE2=EH•EA;(3)、若⊙O的半径为5,sinA= , 求BH的长。
26. 如图,在平面直角坐标系中,抛物线 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点 在抛物线上. (1)、求直线 的解析式.(2)、点P为直线 下方抛物线上的一点,连接 , .当 的面积最大时,连接 , ,点K是线段 的中点,点M是线段 上的一点,点N是线段 上的一点,求 的最小值.(3)、点G是线段 的中点,将抛物线 与x轴正方向平移得到新抛物线 , 经过点 , 的顶点为点F,在新抛物线 的对称轴上,是否存在点Q,使得 为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、求直线 的解析式.(2)、点P为直线 下方抛物线上的一点,连接 , .当 的面积最大时,连接 , ,点K是线段 的中点,点M是线段 上的一点,点N是线段 上的一点,求 的最小值.(3)、点G是线段 的中点,将抛物线 与x轴正方向平移得到新抛物线 , 经过点 , 的顶点为点F,在新抛物线 的对称轴上,是否存在点Q,使得 为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.