四川省雅安市2021-2022学年八年级下学期第二次月考数学试题

试卷更新日期：2023-02-16 类型：月考试卷

进入出卷网下载

一、单选题

1. 不等式 $2 x - 4 > 0$ 的解集是（）

A、 $x < 2$ B、 $x > 2$ C、 $x < - 2$ D、 $x > - 2$

查看试题解析
2. 下列长度的三条线段能组成直角三角形的是（）

A、9，12，15 B、3，4，6 C、8，15，16 D、7，24，26

查看试题解析
3. 下列数表达式① $3 x + 4 y < 0$ ；② $y = 3$ ；③ $2 x + 3 < y$ ；④ $x^{2} + 2 x y + y^{2}$ .其中属于不等式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 在△ABC内一点P到三边的距离相等，则点P一定是△ABC（　　）

A、三条角平分线的交点 B、三边垂直平分线的交点 C、三条高的交点 D、三条中线的交点

查看试题解析
5. 如图，在 $△$ ABC中，边BC的垂直平分线分别交AC，BC于点D，E，若 $△$ ABC的周长为12，CE $= \frac{5}{2}$ ，则 $△$ ABD的周长为（）

A、10 B、9 C、8 D、7

查看试题解析
6. x与5的和不大于-1，用不等式表示为（）

A、 $x + 5 \geq - 1$ B、 $x + 5 < - 1$ C、 $x + 5 \neq - 1$ D、 $x + 5 \leq - 1$

查看试题解析
7. 2020年是我国完成第一个100年奋斗目标的关键之年，到2021年我国全面建成小康社会.人民生活水平越来越高，我国拥有汽车的居民家庭也越来越多，下列汽车标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 一个等腰三角形的两边长分别是4和9，则它的周长为（）

A、17 B、22 C、27 D、17或22

查看试题解析
9. 如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D，若PD＝2，则点P到边OA的距离是（）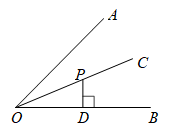

A、2 B、3 C、 $\sqrt{3}$ D、4

查看试题解析
10. 下列命题正确的是（）

A、若 $m c > n c$ ，则 $m > n$ B、若 $m > n$ ，则 $m c^{2} > n c^{2}$ C、若 $m > b$ ， $b < c$ ，则 $m > c$ D、若 $m - n > m$ ，则 $n < 0$

查看试题解析
11. 如图，将30°的直角板 $A B C$ 绕点B按顺时针转动一个角度到 $A_{1} B C_{1}$ 的位置，使得点A、B、 $C_{1}$ 在同一条直线上，那么这个角度等于（）

A、30° B、60° C、90° D、120°

查看试题解析
12. 如图，P是 $Δ A B C$ 的三条角平分线的交点，连接 $P A$ 、 $P B$ 、 $P C$ ，若 $Δ P A B ， Δ P B C ， Δ P A C$ 面积分别为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ ，则（）

A、 $S_{1} < S_{2} + S_{3}$ B、 $S_{1} = S_{2} + S_{3}$ C、 $S_{1} > S_{2} + S_{3}$ D、无法确定 $S_{1}$ 与 $(S_{2} + S_{3})$ 的大小

查看试题解析

二、填空题

13. 如图，将 $Δ A B C$ 绕点 $A$ 顺时针旋转 $60^{\circ}$ 得到 $Δ A E D$ ，则 $∠ C A D =$ $^{\circ}$

查看试题解析
14. 一个等腰三角形的一腰上的高与另一腰的夹角为40°，则它的顶角为：．

查看试题解析
15. 如图，已知 O 为△ABC 三边垂直平分线的交点，且∠A＝50°，则∠BOC 的度数为度.

查看试题解析
16. 若不等式 $3 x - a \leq 0$ 的正整数解是 $1 ， 2 ， 3$ ，则a的取值范围是.

查看试题解析
17. 边长为6cm的等边三角形中，其一边上高的长度为.

查看试题解析
18. 已知关于x的不等式组 ${\begin{array}{l} x - a \geq b \\ 2 x - a < 2 b + 1 \end{array}$ 的解集为3≤x＜5，则 $\frac{a}{b}$ 的值为.

查看试题解析

三、解答题

19.

(1)、解不等式： $5 x + 3 ＜ 3 （ 2 + x ）$ ，并把解表示在数轴上

(2)、解不等式组： ${\begin{array}{l} 2 x + 1 ＜ 3 x + 3 \\ \frac{x + 1}{2} \leq \frac{1 - x}{6} + 1 \end{array}$

查看试题解析
20. 如图，在边长为1的小正方形组成的网格中 $△$ ABC的三个顶点均在格点上，点A，B的坐标分别为A(-2，4)，B(-3，2).

(1)、画出坐标轴，画出 $△$ ABC绕点C顺时针旋转90°后 $△ A^{'} B^{'} C^{'}$ ；

(2)、点 $A ′$ 的坐标为；

(3)、四边形 $A C A^{'} B^{'}$ 的面积为.

查看试题解析
21. 已知锐角△ABC的两条高BE，CD相交于点O，且OB=OC.求证：△ABC是等腰三角形.

查看试题解析
22. 若不等式 $5 (x - 2) + 8 ⩽ 6 (x - 1) + 7$ 的最小整数解是方程 $3 x - a x = - 3$ 的解，求 $- | 10 - a^{2} |$ 的值.

查看试题解析
23. 如图， $D E ⊥ A B$ 于E， $D F ⊥ A C$ 于F，若 $B D = C D$ 、 $B E = C F$ ，

(1)、求证： $A D$ 平分 $∠ B A C$ ；

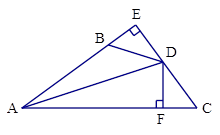(2)、写出 $A B + A C$ 与 $A E$ 之间的等量关系，并说明理由。

查看试题解析
24. 两块等腰直角三角形纸片AOB和COD按图①所示放置，直角顶点重合在点O处，AB＝25.保持纸片AOB不动，将纸片COD绕点O逆时针旋转α(0°＜α＜90°)角度，如图②所示.

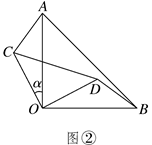
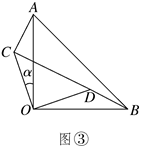(1)、在图②中，求证：AC＝BD，且AC⊥BD；

(2)、当BD与CD在同一直线上(如图③)时，若AC＝7，求CD的长.

查看试题解析
25. 市园林处为了对一段公路进行绿化，计划购买A，B两种风景树共900棵．A，B两种树的相关信息如下表：
品种项目
单价（元/棵）
成活率
A
80
92%
B
100
98%
若购买A种树x棵，购树所需的总费用为y元．

(1)、求y与x之间的函数关系式；

(2)、若购树的总费用不超过82 000元，则购A种树不少于多少棵？

(3)、若希望这批树的成活率不低于94%，且使购树的总费用最低，应选购A，B两种树各多少棵？此时最低费用为多少？

查看试题解析

品种项目	单价（元/棵）	成活率
A	80	92%
B	100	98%