2023年中考数学精选真题实战测试43 正方形 A
试卷更新日期:2023-02-15 类型:二轮复习
一、单选题(每题3分,共30分)
-
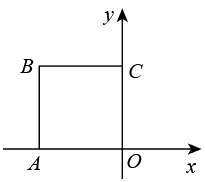
1. 下列说法错误的是( )A、对角线垂直且互相平分的四边形是菱形 B、同圆或等圆中,同弧对应的圆周角相等 C、对角线相等的四边形是矩形 D、对角线垂直且相等的平行四边形是正方形2. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
 A、 B、 C、 D、3. 如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )
A、 B、 C、 D、3. 如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )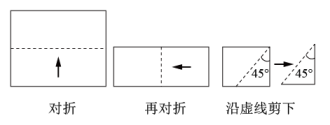 A、三角形 B、梯形 C、正方形 D、五边形4. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A、三角形 B、梯形 C、正方形 D、五边形4. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )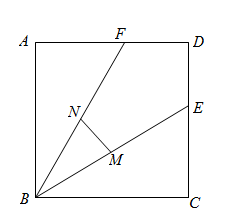 A、 B、 C、 D、5. 如图,在矩形中, , 点E,F分别在边上, , AF与相交于点O,连接 , 若 , 则与之间的数量关系正确的是( )
A、 B、 C、 D、5. 如图,在矩形中, , 点E,F分别在边上, , AF与相交于点O,连接 , 若 , 则与之间的数量关系正确的是( )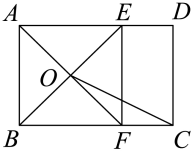 A、 B、 C、 D、6. 若顺次连接四边形 各边的中点所得的四边形是正方形,则四边形 的两条对角线 一定是( )A、互相平分 B、互相垂直 C、互相平分且相等 D、互相垂直且相等7. 如图,在边长为2的等边三角形的外侧作正方形 , 过点作 , 垂足为 , 则的长为( )
A、 B、 C、 D、6. 若顺次连接四边形 各边的中点所得的四边形是正方形,则四边形 的两条对角线 一定是( )A、互相平分 B、互相垂直 C、互相平分且相等 D、互相垂直且相等7. 如图,在边长为2的等边三角形的外侧作正方形 , 过点作 , 垂足为 , 则的长为( ) A、 B、 C、 D、8. 正方形的对角线相交于点O(如图1),如果绕点O按顺时针方向旋转,其两边分别与边相交于点E、F(如图2),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是( )
A、 B、 C、 D、8. 正方形的对角线相交于点O(如图1),如果绕点O按顺时针方向旋转,其两边分别与边相交于点E、F(如图2),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是( ) A、线段 B、圆弧 C、折线 D、波浪线9. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )
A、线段 B、圆弧 C、折线 D、波浪线9. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC、GA,交于点O,GA与BC交于点P,连接OD、OB,则下列结论一定正确的是( )①EC⊥AG;②△OBP∽△CAP;③OB平分∠CBG;④∠AOD=45°;
 A、①③ B、①②③ C、②③ D、①②④10. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:
A、①③ B、①②③ C、②③ D、①②④10. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:①;②;③;④.其中正确结论的个数为( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共18分)
-
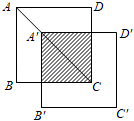
11. 如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′=AC,则所得正方形与原正方形重叠部分的面积是 .
 12. 如图,在直角坐标系中,边长为2个单位长度的正方形绕原点O逆时针旋转 , 再沿y轴方向向上平移1个单位长度,则点的坐标为 .
12. 如图,在直角坐标系中,边长为2个单位长度的正方形绕原点O逆时针旋转 , 再沿y轴方向向上平移1个单位长度,则点的坐标为 .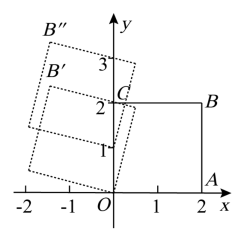 13. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .
13. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .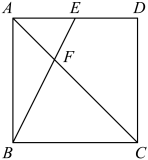 14. 如图,四边形ABCD是正方形,点E在边BC的延长线上,点F在边AB上,以点D为中心将绕点D顺时针旋转与恰好完全重合,连接EF交DC于点P,连接AC交EF于点Q,连接BQ,若 , 则.
14. 如图,四边形ABCD是正方形,点E在边BC的延长线上,点F在边AB上,以点D为中心将绕点D顺时针旋转与恰好完全重合,连接EF交DC于点P,连接AC交EF于点Q,连接BQ,若 , 则. 15. 如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .
15. 如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .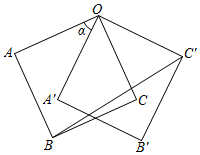 16. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:
16. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:①四边形是平行四边形;
②当时,四边形是矩形;
③当时,四边形是菱形;
④当 , 且时,四边形是正方形.
其中正确结论有(填上所有正确结论的序号).

三、解答题(共8题,共72分)
-
17. 如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
 18. 如图,在正方形中,为上一点,连接 , 的垂直平分线交于点 , 交于点 , 垂足为 , 点在上,且.
18. 如图,在正方形中,为上一点,连接 , 的垂直平分线交于点 , 交于点 , 垂足为 , 点在上,且. (1)、求证:;(2)、若 , , 求的长.19. 如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.
(1)、求证:;(2)、若 , , 求的长.19. 如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.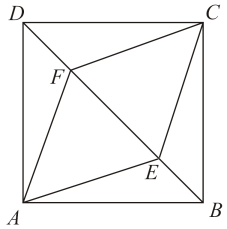 (1)、求证:△ABE≌△CDF;(2)、若AB=3 , BE=2,求四边形AECF的面积.20. 将正方形和菱形按照如图所示摆放,顶点D与顶点H重合,菱形的对角线经过点B,点E,G分别在 , 上.
(1)、求证:△ABE≌△CDF;(2)、若AB=3 , BE=2,求四边形AECF的面积.20. 将正方形和菱形按照如图所示摆放,顶点D与顶点H重合,菱形的对角线经过点B,点E,G分别在 , 上.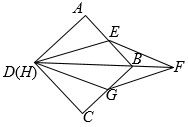 (1)、求证:;(2)、若 , 求的长.21. 如图,点E是正方形ABCD的边BC上的动点, ,且 , .
(1)、求证:;(2)、若 , 求的长.21. 如图,点E是正方形ABCD的边BC上的动点, ,且 , .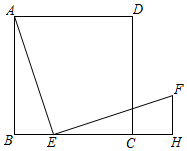 (1)、求证: ;(2)、若 , ,用x表示DF的长.22.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证:
(1)、求证: ;(2)、若 , ,用x表示DF的长.22.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证: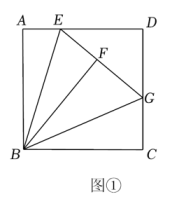 (2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长. (3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长.
(3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长. 23. 已知是的角平分线,点E,F分别在边 , 上, , , 与的面积之和为S.
23. 已知是的角平分线,点E,F分别在边 , 上, , , 与的面积之和为S. (1)、填空:当 , , 时,
(1)、填空:当 , , 时,①如图1,若 , , 则 , ;
②如图2,若 , , 则 , ;
(2)、如图3,当时,探究S与m、n的数量关系,并说明理由:(3)、如图4,当 , , , 时,请直接写出S的大小.24. 已知正方形 , 为对角线 上一点.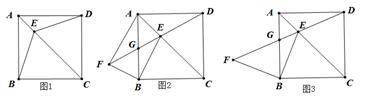 (1)、【建立模型】如图1,连接 , .求证: ;(2)、【模型应用】如图2, 是 延长线上一点, , 交 于点 .
(1)、【建立模型】如图1,连接 , .求证: ;(2)、【模型应用】如图2, 是 延长线上一点, , 交 于点 .①判断 的形状并说明理由;
②若 为 的中点,且 ,求 的长.
(3)、【模型迁移】如图3, 是 延长线上一点, , 交 于点 , .求证: .