人教A版（2019）必修第二册《6.1平面向量的概念》同步练习

试卷更新日期：2023-02-15 类型：同步测试

进入出卷网下载

一、单选题（本大题共8小题，共40分）

1. 设向量 $\vec{a} = (3 ， - 3)$ ， $\vec{b} = (- 2 ， 6)$ ，则 $| 2 \vec{a} + \vec{b} | =$ （）

A、2 B、4 C、8 D、16

查看试题解析
2. 若向量 $\vec{a} = (\frac{1}{x} ， 1)$ 与 $\vec{b} = (2 ， y)$ 平行，则点 $(x ， y)$ 和点 $(1 ， 1)$ 间距离的最小值为（）

A、 $\frac{\sqrt{5}}{5}$ B、1 C、 $\frac{3 \sqrt{5}}{5}$ D、 $\sqrt{2}$

查看试题解析
3. 设四边形ABCD中，有 $\vec{D C}$ = $\frac{1}{2} \vec{A B}$ 且| $\vec{A D}$ |=| $\vec{B C}$ |，则这个四边形是（）

A、平行四边形 B、矩形 C、等腰梯形 D、菱形

查看试题解析
4. 已知点 $A (1 ， 3)$ ， $B (- 2 ， 7)$ ，则与向量 $\vec{AB}$ 方向相反的单位向量是（）

A、 $(\frac{4}{5} ， - \frac{3}{5})$ B、 $(3 ， - 4)$ C、 $(- \frac{3}{5} ， \frac{4}{5})$ D、 $(\frac{3}{5} ， - \frac{4}{5})$

查看试题解析
5. 如果向量 $\vec{a} = (k ， 1)$ 与 $\vec{b} = (4 ， k)$ 共线且方向相反，则 $k =$ （）

A、±2 B、-2 C、2 D、0

查看试题解析
6. 下列说法正确的是（）

A、若 $| \vec{a} | = | \vec{b} |$ ，则 $\vec{a}$ ， $\vec{b}$ 的长度相等且方向相同或相反 B、若向量 $\vec{AB}$ ， $\vec{CD}$ 满足 $| \vec{AB} | > | \vec{CD} |$ ，且 $\vec{AB}$ 与 $\vec{CD}$ 同向，则 $\vec{AB} > \vec{CD}$ C、若 $\vec{a} \neq \vec{b}$ ，则 $\vec{a}$ 与 $\vec{b}$ 可能是共线向量 D、若零向量 $\vec{AB}$ 与 $\vec{CD}$ 共线，则 $A$ ， $B$ ， $C$ ， $D$ 四点共线

查看试题解析
7. 已知向量 $\vec{a} = (x ， 1)$ ， $\vec{b} = (4 ， x)$ ，若向量 $\vec{a}$ 和 $\vec{b}$ 方向相同，则实数 $x$ 的值是（）

A、-2 B、2 C、0 D、 $\frac{8}{5}$

查看试题解析
8. 质点 $P$ 在平面上作匀速直线运动，速度向量 $\vec{v} = (4 ， - 3) ($ 即点 $P$ 的运动方向与 $\vec{v}$ 相同，且每秒移动的距离为 $| \vec{v} |$ 个单位 $) .$ 设开始时点 $P$ 的坐标为 $(- 10 ， 10)$ ，则5秒后点 $P$ 的坐标为（）

A、 $(- 2 ， 4)$ B、 $(- 30 ， 25)$ C、 $(10 ， - 5)$ D、 $(5 ， - 10)$

查看试题解析

二、多选题（本大题共5小题，共25分）

9. 下列结论正确的是（）

A、向量不能比较大小，但向量的模可以比较大小． B、 $| \vec{a} |$ 与 $| \vec{b} |$ 是否相等与 $\vec{a}$ ， $\vec{b}$ 的方向无关． C、若 $\vec{a} // \vec{b}$ ， $\vec{b} // \vec{c}$ ，则 $\vec{a} // \vec{c}$ . D、若向量 $\vec{AB}$ 与向量 $\vec{CD}$ 是共线向量，则 $A$ ， $B$ ， $C$ ， $D$ 四点在一条直线上．

查看试题解析
10. 如图所示，四边形 $ABCD$ ， $CEFG$ ， $CGHD$ 是全等的菱形，则下列结论中一定成立的是（）

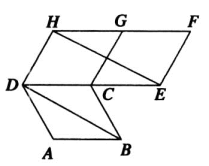A、 $| \vec{AB} |=| \vec{EF} |$ B、 $\vec{AB}$ 与 $\vec{FH}$ 共线 C、 $\vec{BD}$ 与 $\vec{EH}$ 共线 D、 $\vec{CD} = \vec{FG}$

查看试题解析
11. 下列命题中，不正确的是（）

A、同起点的两个非零向量不共线 B、向量 $\vec{a}$ 与 $\vec{b}$ 不共线，则 $\vec{a}$ 与 $\vec{b}$ 都是非零向量 C、若 $\vec{a}$ 与 $\vec{b}$ 共线， $\vec{b}$ 与 $\vec{c}$ .共线，则 $\vec{a}$ .与 $\vec{c}$ .共线 D、“ $\vec{a} = \vec{b}$ ”的充要条件是 $| \vec{a} | = | \vec{b} |$ 且 $\vec{a} / / \vec{b}$

查看试题解析
12. 下列说法正确的是（）

A、长度相等的向量不是相等向量 B、共线向量是在同一直线上的向量 C、零向量的长度等于 $0$ D、 $\vec{A B} / / \vec{C D}$ ，就是 $\vec{A B}$ 所在的直线平行或者于 $\vec{C D}$ 所在的直线

查看试题解析
13. 已知 $Q$ 为坐标原点，点 $A (1 ， 0)$ ， $P_{1} (cos α ， sin α)$ ， $P_{2} (cos β ， - sin β)$ ， $P_{3} (cos (α + β) ， sin (α + β))$ ，则（）

A、 $| \vec{O P_{1}} | = | \vec{O P_{2}} |$ B、 $| \vec{A P_{1}} | = | \vec{A P_{2}} |$ C、 $| \vec{A P_{1}} | = | \vec{P_{2} P_{3}} |$ D、 $| \vec{A P_{3}} | = | \vec{P_{1} P_{2}} |$

查看试题解析

三、填空题（本大题共5小题，共25分）

14. 已知向量 $\vec{e_{1}} ， \vec{e_{2}}$ 是两个不共线的向量，若向量 $\vec{a} = 2 \vec{e_{1}} - \vec{e_{2}}$ 与向量 $\vec{b} = 3 \vec{e_{1}} + λ \vec{e_{2}}$ 共线，则实数 $λ =$ ．

查看试题解析
15. 给出下列六个命题：
①两个向量相等，则它们的起点相同，终点相同；

②若 $| \vec{a} | = | \vec{b} |$ ，则 $\vec{a} = \vec{b}$ ；

③若 $\vec{AB} = \vec{DC}$ ，则 $A$ ， $B$ ， $C$ ， $D$ 四点构成平行四边形；

④在平行四边形 $ABCD$ 中，一定有 $\vec{AB} = \vec{DC}$ ；

⑤若 $\vec{m} = \vec{n}$ ， $\vec{n} = \vec{p}$ ，则 $\vec{m} = \vec{p}$ ；

⑥若向 $\vec{a} // \vec{b}$ ， $\vec{b} // \vec{c}$ ，则 $\vec{a} // \vec{c}$ ．

其中错误的命题有 $. ($ 填序号 $)$

查看试题解析
16. 已知平行四边形ABCD的三个顶点A（-3，-1），B（2，-1），C（5，3），求顶点D的坐标为．

查看试题解析
17. 已知 $\vec{a} = (- 1 ， 2)$ ， $\vec{b} = (3 ， - 1)$ ，则与 $\vec{a} - \vec{b}$ 同方向的单位向量是．

查看试题解析
18. 给出下列命题：①两个单位向量一定相等；②若向量 $a$ 与 $b$ 不共线，则 $a$ 与 $b$ 都是非零向量；③共线的单位向量必相等；④两个相等的向量起点、方向、长度必须都相同．其中正确的命题是.（填序号）

查看试题解析

四、解答题（本大题共5小题，共60分）

19. 如图所示，已知空间四边形 $A B C D$ ， $E$ ， $H$ 分别是边 $A B$ ， $A D$ 的中点， $F$ ， $G$ 分别是边 $C B$ ， $C D$ 上的点，且 $\vec{C F} = 2 \vec{F B}$ ， $\vec{C G} = 2 \vec{G D} .$ 证明：四边形 $E F G H$ 是梯形．

查看试题解析
20. 如图， $O$ 为正方形 $ABCD$ 对角线的交点，四边形 $OAED$ ， $OCFB$ 都是正方形，在图中所示的向量中：求：

(1)、写出相等的向量；

(2)、与 $\vec{AO}$ 共线的向量；

(3)、模相等的向量；

(4)、 $\vec{AO}$ 与 $\vec{CO}$ 是否为相等向量．

查看试题解析
21. 边长为1的正三角形 $ABC$ ， $E$ 、 $F$ 分别是边 $AB$ 、 $AC$ 上的点，若 $\vec{AE} = m \vec{AB}$ ， $\vec{AF} = n \vec{AC}$ ，其中 $m$ ， $n \in (0 ， 1)$ ，设 $EF$ 的中点为 $M$ ， $BC$ 中点为 $N .$

(1)、若 $A$ 、 $M$ 、 $N$ 三点共线，求证： $m = n；$

(2)、若 $m + n = 1$ ，求 $| MN |$ 的最小值.

查看试题解析
22. 一辆汽车从 $A$ 点出发向西行驶了 $100km$ 到达 $B$ 点，然后又改变方向向西偏北 $50 °$ 走了 $200km$ 到达 $C$ 点，最后又改变方向，向东行驶了 $100km$ 到达 $D$ 点.

(1)、作出向量 $\vec{AB}$ 、 $\vec{BC}$ 、 $\vec{CD}$ ；

(2)、求 $| \vec{AD} | .$

查看试题解析
23. 一条宽为 $\sqrt{3}$ km的河，水流速度为2km/h，在河两岸有两个码头A、B，已知AB= $\sqrt{3}$ km，船在水中最大航速为4km/h，问该船从A码头到B码头怎样安排航行速度可使它最快到达彼岸B码头？用时多少？

查看试题解析