2023年中考数学精选真题实战测试41 矩形 A
试卷更新日期:2023-02-14 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 在下列条件中,能够判定为矩形的是( )A、 B、 C、 D、
-
2. 如图,在中, , 的平分线交于点 , 为的中点,若 , 则的长是( )
 A、8 B、6 C、5 D、4
A、8 B、6 C、5 D、4 -
3. 要检验一个四边形的桌面是否为矩形,可行的测量方案是( )A、测量两条对角线是否相等 B、度量两个角是否是90° C、测量两条对角线的交点到四个顶点的距离是否相等 D、测量两组对边是否分别相等
-
4. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )
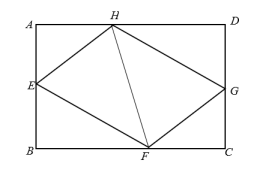 A、 B、 C、 D、
A、 B、 C、 D、 -
5. 如图所示,将一矩形纸片沿AB折叠,已知 , 则( )
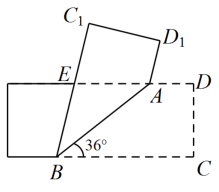 A、48° B、66° C、72° D、78°
A、48° B、66° C、72° D、78° -
6. 如图,在矩形中, , 点E,F分别在边上, , AF与相交于点O,连接 , 若 , 则与之间的数量关系正确的是( )
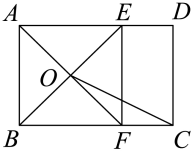 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
 A、BD=10 B、HG=2 C、EG∥FH D、GF⊥BC
A、BD=10 B、HG=2 C、EG∥FH D、GF⊥BC -
8. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( )
 A、9 B、12 C、15 D、18
A、9 B、12 C、15 D、18 -
9. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个 -
10. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:
① ;② ;③ ;④ ;⑤ .
其中正确的是( )
 A、①②③ B、①③④ C、①④⑤ D、②③④
A、①②③ B、①③④ C、①④⑤ D、②③④
二、填空题(每空3分,共18分)
-
11. 如图,在和中, , 、、分别为、、的中点,若 , 则 .

-
12. 如图矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=3,BC=4,则图中阴影部分的面积为 .

-
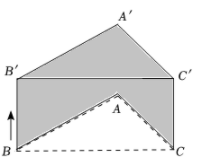
13. 如图, △ABC的边BC长为4cm.将△ABC平移2cm得到△A′B′C′ ,且BB′⊥BC,则阴影部分的面积为 .
-
14. 如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得 ,连接 ,当 时, 是以 为腰的等腰三角形.
-
15. 如图,在矩形中,=6,=8,点、分别是边、的中点,某一时刻,动点从点出发,沿方向以每秒2个单位长度的速度向点匀速运动;同时,动点从点出发,沿方向以每秒1个单位长度的速度向点匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接 , 过点作的垂线,垂足为.在这一运动过程中,点所经过的路径长是.
-
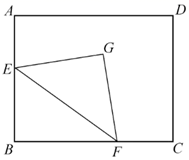
16. 如图,在矩形 中, ,点E,F分别是边 上的动点,点E不与A,B重合,且 ,G是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点G到边 的距离一定相等;
③点G到边 的距离可能相等;
④点G到边 的距离的最大值为 .
其中正确的是.(写出所有正确结论的序号)
三、解答题(共8题,共72分)
-
17. 如图,在矩形ABCD中,对角线AC、BD相交于点O,且∠CDF=∠BDC、∠DCF=∠ACD.
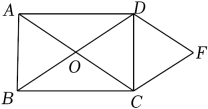 (1)、求证:DF=CF;(2)、若∠CDF=60°,DF=6,求矩形ABCD的面积.
(1)、求证:DF=CF;(2)、若∠CDF=60°,DF=6,求矩形ABCD的面积. -
18. 如图,将矩形ABCD沿对角线AC折叠,点B的对应点为E,AE与CD交于点F.
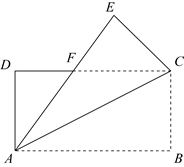 (1)、求证: ;(2)、若 ,求 的度数.
(1)、求证: ;(2)、若 ,求 的度数. -
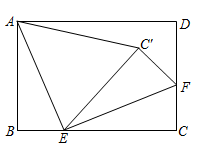
19. 如图,将一张长方形纸片 沿 折叠,使 两点重合.点 落在点 处.已知 , .
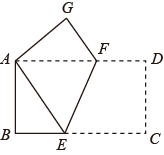 (1)、求证: 是等腰三角形;(2)、求线段 的长.
(1)、求证: 是等腰三角形;(2)、求线段 的长. -
20. 如图, 为等腰直角三角形,延长 至点B使 ,其对角线 , 交于点E.
 (1)、求证: ;(2)、求 的值.
(1)、求证: ;(2)、求 的值. -
21. 如图:
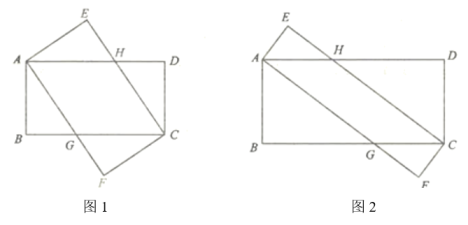 (1)、将两张长为8,宽为4的矩形纸片如图1叠放.
(1)、将两张长为8,宽为4的矩形纸片如图1叠放.①判断四边形AGCH的形状,并说明理由;
②求四边形AGCH的面积.
(2)、如图2,在矩形ABCD和矩形AFCE中,AB=2 , BC=7,CF= , 求四边形AGCH的面积. -
22. 在四边形中,的平分线交于 , 延长到使 , 是的中点,交于 , 连接.
 (1)、当四边形是矩形时,如图,求证:①;②.(2)、当四边形是平行四边形时,如图,(1)中的结论都成立,请给出结论②的证明.
(1)、当四边形是矩形时,如图,求证:①;②.(2)、当四边形是平行四边形时,如图,(1)中的结论都成立,请给出结论②的证明. -
23. 问题背景:
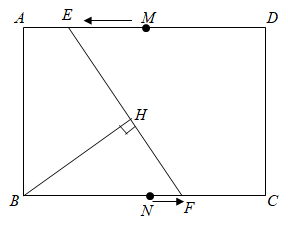
如图1,在矩形中, , , 点E是边AB的中点,过点作交BD于点F.
 (1)、实验探究:
(1)、实验探究:在一次数学活动中,小王同学将图1中的绕点按逆时针方向旋转 , 如图2所示,得到结论:①;②直线AE与DF所夹锐角的度数为 .
(2)、小王同学继续将绕点B按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立?并说明理由.(3)、拓展延伸:在以上探究中,当旋转至、、三点共线时,则的面积为 .
-
24. 在矩形 中, , ,F是对角线 上不与点A,C重合的一点,过F作 于E,将 沿 翻折得到 ,点G在射线 上,连接 .(1)、如图1,若点A的对称点G落在 上, ,延长 交 于H,连接 .

①求证: ;
②求 .
(2)、如图2,若点A的对称点G落在 延长线上, ,判断 与 是否全等,并说明理由.
