浙江省温州市2022-2023学年八年级上学期数学期末试题
试卷更新日期：2023-02-14 类型：期末考试
一、选择题(本题有10小题，每小题3分，共30分．)
-
1. 下列运动图标中，属于轴对称图形的是（ ）A、
B、
C、
D、
2. 两根木棒的长度分别为5cm，8cm，取第三根木棒，使它们首尾顺次相接组成一个三角形，则第三根木棒的长度可以是（ ）A、2cm B、3cm C、6cm D、15cm3. 函数y= 中自变量x的取值范围是（ ）A、x≠-2 B、x≠2 C、x<2 D、x>24. 若x>y，则下列不等式成立的是（ ）A、-2x>-2y B、x-6<y- 6 C、x-y<0 D、5. 下列命题属于假命题的是（ ）A、三个角对应相等的两个三角形全等 B、三边对应相等的两个三角形全等 C、全等三角形的对应边相等 D、全等三角形的面积相等6. 如图是某纸伞截面示意图，伞柄AP平分两条伞骨所成的角∠BAC．若支杆DF需要更换，则所换长度应与哪一段长度相等（ ）
A、BE B、AE C、DE D、DP7. 如图是画在方格纸上的温州部分旅游景点简图．建立直角坐标系后，狮子岩、永嘉书院与埭头古村的坐标分别是(3，2)，(-1，-3)，(-3，0)，下列地点中离原点最近的是（ ）
A、狮子岩 B、龙瀑仙洞 C、埭头古村 D、永嘉书院8. 如图，小亮进行以下操作：以点A为圆心，适当长为半径作圆弧分别交AB， AC于点D，E；分别以点D，E为圆心，大于DE长为半径作圆弧，两条圆弧交于∠BAC内一点F，作射线AF．若∠BDF=50°，∠EFD-∠BAC=24°，则∠BAC等于（ ）
A、26° B、31° C、37° D、38°9. 已知点(a，b)，(a+1，c)在一次函数y=2x-3的图象上，则函数y= 4x+c-b的图象不经过（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图，大正方形ABCD由四个全等的直角三角形和一个小正方形拼接而成．点E为小正方形的顶点，延长CE交AD于点F，连结BF交小正方形的一边于点G．若△BCF为等腰三角形，AG=5，则小正方形的面积为（ ）
A、15 B、16 C、20 D、25二、填空题(本题有8小题，每小题3分，共24分)
-
11. “a的3倍与2的差小于9”用不等式表示为 ．12. 点(7，11)向右平移1个单位后所得点的坐标是 ．13. 一张小凳子的结构如图所示，AC=BC，∠1=100°， 则∠2=°．
14. 若一个三角形三个内角的度数之比为1：2：3，则这个三角形是三角形(填“锐角”、“直角”或“钝角”) ．15. 已知一次函数y=-3x+1，当4≤y≤10时，x的最大值为16. 某种气体的体积y (L)与气体的温度x (C)对应值如下表．若要使气体的体积至少为106升，则气体的温度不低于℃．x(℃)
……
0
1
2
3
……
10
……
y(L)
……
100
100.3
100.6
100.9
……
103
……
17. 如图，在等腰三角形ABC中，AD是底边BC上的高线，CE⊥AB于点E，交AD于点F．若∠BAC=45°，AF=6，则BD的长为
18. 如图1，小明将一张长方形纸片对折，使长方形两边重合，折痕为EF，铺开后沿BC折叠，使点A与EF上的点D重合．如图2，再将该长方形纸片进行折叠，折痕分别为HG，KL，使长方形的两边均与EF重合；铺开后沿BP折叠，使点A与KL上的点Q重合；分别连结图1中的AD与图2中的AQ，则的值为.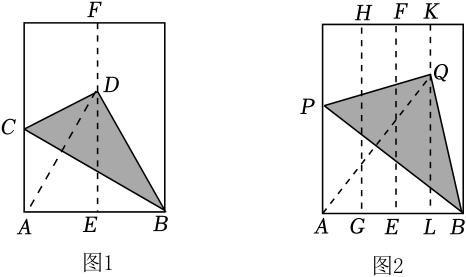
三、解答题(本题有5小题，共46分.)
-
19. 解一元一次不等式组 ， 并把解表示在数轴上．
20. 如图，△ABC是等边三角形，将BC向两端延长至点D，E，使BD=CE，连结AD，AE．求证：∠D=∠E．
21. 在直角坐标系中，我们把横坐标、纵坐标均为整数的点称为整点．如图，直线AB分别与x轴、y轴交于点A (-3，0)，B(0，4)． 请在所给的网格区域(含边界)作图．
(1)、画一个等腰三角形ABC， 且点C为第一象限内的整点，并写出点C的坐标．(2)、画一个△OAD，使△OAD与△AOB重叠部分的面积是△AOB面积的一半，且点D为整点，并写出点D的坐标．22. 探究通过维修路段的最短时长．素材1：如图1，某路段(A-B-C-D 段)需要维修，临时变成双向交替通行，故在A，D处各设置红绿灯指导交通(仅设置红灯与绿灯)．
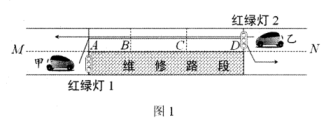
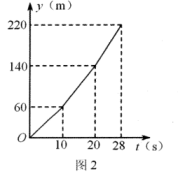
素材2：甲车先由A→D通行，乙车再由D→A通行，甲车经过AB，BC，CD段的时间分别为10s，10s，8s，它的路程y (m)与时间t(s)的关系如图2所示；两车经过BC段的速度相等，乙车经过AB段的速度是10m/s．
素材3：红绿灯1，2每114秒一个循环，每个循环内红灯、绿灯的时长如图3，且每次双向红灯时，已经进入AD段的车辆都能及时通过该路段．
[任务1]求A-B-C-D段的总路程和甲车经过BC段的速度．
[任务2]在图4中补全乙车通过维修路段时行驶的路程y(m)与时间t(s)之间的函数图象．
[任务3]丙车沿NM方向行驶，经DA段的车速与乙车经过时的速度相同，在DN段等红灯的车辆开始行驶后速度为8m/s，等红灯时车流长度每秒增加2m，问丙车在DN段从开始等待至离开点A至少需要几秒钟？
23. 如图，将一块含45°角的直角三角板AOB放置在直角坐标系中，其直角顶点O与原点重合，点A落在第一象限，点B的坐标为(-2，6)，AB与y轴交于点C．
(1)、求点A的坐标．(2)、求OC的长．(3)、点P在x轴正半轴上，连结AP．当∠PAO与△COB的一个内角相等时，求所有满足条件的OP的长．