四川省成都市龙泉驿区2022-2023学年九年级上学期期末数学试题

试卷更新日期：2023-02-14 类型：期末考试

进入出卷网下载

一、选择题（本大题共8个小题，每小题4分，共32分，）

1. 下列为一元二次方程的是（）

A、 $2 x - x^{2} = 7$ B、2x＋y＝22 C、 $x^{3} + 2 x - 1 = 0$ D、 $x + \frac{1}{y} = 7$

查看试题解析
2. 从左边观察如图所示的几何体，得到的形状图为（）

A、 B、 C、 D、

查看试题解析
3. 一个不透明的箱子里装有m个球，其中红球3个，这些球除颜色不同其余都相同，每次搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验发现，摸到红球的频率稳定在0.3附近，则可以估算出m的值为（）

A、3 B、5 C、10 D、12

查看试题解析
4. 下列各组图形，一定相似的是（）

A、两个等腰梯形 B、两个正方形 C、两个菱形 D、两个矩形

查看试题解析
5. 若关于x的一元二次方程 $(k - 2) x^{2} + 2 x - 1 = 0$ 有实数根，则k的取值范围是（）

A、 $k \leq 1$ B、 $k \leq 1$ 且 $k \neq 2$ C、 $k \geq 1$ 且 $k \neq 2$ D、 $k \geq 2$

查看试题解析
6. 如果两个相似三角形的面积之比为9：4，那么这两个三角形对应边上的高之比为（）

A、9：4 B、3：2 C、2：3 D、81：16

查看试题解析
7. 某市某鞋厂10月份的运动鞋产量为24万双，因销量较好，11月份、12月份均增大产量，使第四季度的总产量达到88万双设该厂11、12月份的运动鞋产量的月平均增长率为x，根据题意可列方程为（）

A、 $88 {(1 + x)}^{2} = 24$ B、 $88 {(1 - x)}^{2} = 24$ C、 $24 {(1 + x)}^{2} = 88$ D、 $24 + 24 (1 + x) + 24 {(1 + x)}^{2} = 88$

查看试题解析
8. 在同一直角坐标系中，一次函数y＝kx—k与反比例函数 $y = \frac{k}{x}$ （ $k \neq 0$ ）的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共5个小题，每小题4分，共20分.）．

9. 反比例函数 $y = \frac{m + 1}{x}$ 的图象在第一、三象限，则 $m$ 的取值范围是．

查看试题解析
10. 若四条线段a，b，c，d成比例，其中 $b = 3$ ， $c = 4$ ， $d = 6$ ，则 $a =$ ．

查看试题解析
11. 反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 两点，当 $x_{1} < 0 < x_{2}$ 时， $y_{1} > y_{2}$ ，写出符合条件的 $k$ 的值（答案不唯一，写出一个即可）．

查看试题解析
12. 如图，矩形ABCD的对角线AC，BD相交于点O， $O F ⊥ A B$ ，垂足为点F， $B E ⊥ A C$ ，垂足为点 $E$ ，且E是OC的中点．若 $O F = 2$ ，则BD的长为．

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = 6$ ， $A C = 8$ ， $D$ 是边AB上一点，且 $A D = 2$ ，如果点E在边AC上，且 $△ A D E ∽ △ A B C$ ，那么 $A E$ ＝．

查看试题解析

三、解答题（本大题共5个小题，共48分。）

14. 解方程：

(1)、 $x^{2} - 2 = 7$ ；

(2)、 $x^{2} - 8 x - 20 = 0$ ．

查看试题解析
15. 如图，四边形ABCD中，AD∥BC，AB⊥AC，点E是BC的中点，AE与BD交于点F，且F是AE的中点.
（Ⅰ）求证：四边形AECD是菱形；（Ⅱ）若AC＝4，AB＝5，求四边形ABCD的面积.

查看试题解析
16. 某厂有一批可降解的外卖餐盒准备出售，现从中随机抽取一部分外卖餐盒，根据这些餐盒的价格（单位：元）分别绘制了如图1，图2所示的扇形统计图和条形统计图，相同价格的餐盒除颜色外均相同。请根据相关信息，解答下列问题．

(1)、随机抽取的外卖餐盒的数量为个；图中a的值为；b的值为；

(2)、在这组数据中，价格为2元的外卖餐盒颜色如下：2个白色，1个红色，1个黄色，现从这4个餐盒中随机抽取2个外卖餐盒，请利用画树状图的方法求抽到一个白色餐盒和一个红色餐盒的概率．

查看试题解析
17. 小言家窗外有一个路灯，每天晚上灯光都会透过窗户照进房间里，小言一直想知道这个路灯的准确高度，当学了相似三角形的知识后，她意识到自己可以解决这个问题了！如图，路灯顶部A处发光，光线透过窗子BC照亮地面的长度为DE，小言测得窗户距离地面高度BF＝0.7m，窗高BC＝1.4m，某一时刻，FD＝0.7m，DE＝2.1m，请你根据小言测得的数据，求出路灯的高度OA．

查看试题解析
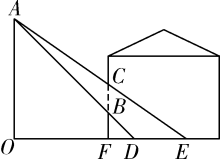18. 如图，一次函数y＝kx＋b与反比例函数 $y = \frac{m}{x}$ （x>0）的图象交于点A（1，a）和点B（2，3），与y轴，x轴分别交于C，D两点，

(1)、求一次函数和反比例函数的表达式；

(2)、点E为反比例函数 $y = \frac{m}{x}$ （x>0）上一点（不与点A，B重合），过点E作EF⊥x轴，垂足为点F，当△EFD∽△OCD时，求点E坐标．

查看试题解析

四、填空题（本大题共5个小题，每小题4分，共20分.）

19. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{4}{5} (b + d \neq 0)$ ，则 $\frac{a - 2 c}{b - 2 d}$ ＝．

查看试题解析
20. 如图，某校给初一年级划了一块大的矩形菜地，年级又将它分为大小形状完全相同的三块分给三个班，同学们测量后惊奇的发现，每块小菜地都与原大矩形菜地相似，则原矩形菜地的宽与长之比为．

查看试题解析
21. 设关于x的方程 $x^{2} - 2 x - m + 1 = 0$ 的两个实数根分别为 $α$ ， $β$ ，若 $| α | + | β | = 6$ ，那么实数m的取值是．

查看试题解析
22. 用换元法解关于x的分式方程 $\frac{x - 1}{x} + \frac{2 a x}{x - 1} - 2 a - 1 = 0$ 时，如果设 $\frac{x - 1}{x} = y$ 将原方程化为关于y的整式方程，那么这个整式方程是，若原方程的解为正数，则a的取值范围为．

查看试题解析
23. 如图，正方形ABCD，AB＝2，点E为AD上一动点，将三角形ABE沿BE折叠，点A落在点F处，连接DF并延长，与边AB交于点G，若点G为AB中点，则AE＝．

查看试题解析

五、解答题（本大题共3个小题，共30分。）

24. 通过实验研究发现：初中生在数学课上听课注意力指标数随上课时间的变化而变化，上课开始时，学生兴趣激增，中间一段时间，学生的兴趣保持平稳状态，随后开始分散，学生注意力指标数y随时间x（分）变化的函数图象如图所示，当 $0 \leq x < 10$ 和 $10 \leq x < 20$ 时，图象是线段；当 $20 \leq x \leq 40$ 时，图象是双曲线的一部分，根据函数图象回答下列问题：

(1)、点A的注意力指标数是；

(2)、当 $0 \leq x < 10$ 时，求注意力指标数y随时间x（分）的函数解析式；

(3)、张老师在一节课上讲解一道数学综合题需要21分钟，他能否经过适当的安排，使学生在听这道综合题的讲解时，注意力指标数都不低于36？请说明理由．

查看试题解析
25. 在△ABC中，点D，E分别在边AB，BC上，连接AE，CD交于点O，且∠ADC＝∠AEC，

(1)、求证： $B D \cdot A B = B E \cdot B C$ ：

(2)、当D为边AB的中点时，且CE＝4
①若2AO＝3OE，求AB
②若△AEC为等腰直角三角形，且∠EAC＝90°，求四边形BDOE的面积．

查看试题解析
26. 某班在“图形与坐标”的主题学习中，第四学习小组提出如下背景“如图，在平面直角坐标系中，将一个边长为2的等边三角形ABC沿x轴平移（边AB在x轴上，点C在x轴上方），其中A（a，0），三角形ABC与反比例函数 $y = \frac{2 \sqrt{3}}{x}$ （x>0）交于点D，E两点（点D在点E左边）”，让其他小组提出问题，请你解答：

(1)、第一小组提出“当a＝2时，求点D的坐标”；

(2)、第二小组提出“若AD＝CE，求a的值”：

(3)、第三小组提出“若将点E绕点A逆时针旋转60°至点 $E^{'}$ ，点 $E^{'}$ 恰好也在 $y = \frac{2 \sqrt{3}}{x}$ （x>0）上，求a的值”；

查看试题解析