陕西省渭南市澄城县2022-2023学年“梦启航”联盟九年级上学期数学期末测试
试卷更新日期:2023-02-14 类型:期末考试
一、选择题(共12题,共48分)
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 是关于 的一元二次方程,则( )A、 B、 C、 D、 且3. 若m是一元二次方程 的根,则代数式 的值为( )A、1 B、-1 C、2 D、-224. “凤鸣”文学社在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,某组共互赠了210本图书,如果设该组共有 名同学,那么依题意,可列出的方程是( )A、 B、 C、 D、5. 要得到抛物线y=2(x-4)2-1,可以将抛物线 ( )A、向左平移4个单位长度,再向上平移1个单位长度 B、向左平移4个单位长度,再向下平移1个单位长度 C、向右平移4个单位长度,再向上平移1个单位长度 D、向右平移4个单位长度,再向下平移1个单位长度6. 在同一平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+5x+b的图象可能是( )A、
2. 若 是关于 的一元二次方程,则( )A、 B、 C、 D、 且3. 若m是一元二次方程 的根,则代数式 的值为( )A、1 B、-1 C、2 D、-224. “凤鸣”文学社在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,某组共互赠了210本图书,如果设该组共有 名同学,那么依题意,可列出的方程是( )A、 B、 C、 D、5. 要得到抛物线y=2(x-4)2-1,可以将抛物线 ( )A、向左平移4个单位长度,再向上平移1个单位长度 B、向左平移4个单位长度,再向下平移1个单位长度 C、向右平移4个单位长度,再向上平移1个单位长度 D、向右平移4个单位长度,再向下平移1个单位长度6. 在同一平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+5x+b的图象可能是( )A、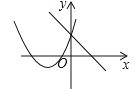 B、
B、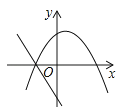 C、
C、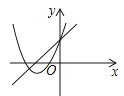 D、
D、 7. 已知二次函数 的图象如图所示,对称轴为 . 下列结论中,正确的是( )
7. 已知二次函数 的图象如图所示,对称轴为 . 下列结论中,正确的是( ) A、 B、 C、 D、8. 如图, 为 的直径, 是 的弦, ,则 的度数为( )
A、 B、 C、 D、8. 如图, 为 的直径, 是 的弦, ,则 的度数为( )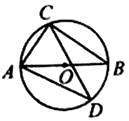 A、 B、 C、 D、9. 如图, 是 的直径, , , , 则阴影部分的面积为( )
A、 B、 C、 D、9. 如图, 是 的直径, , , , 则阴影部分的面积为( ) A、 B、 C、 D、10. 如图显示了用计算机模拟随机投掷一枚图钉的实验结果.随着试验次数的增加,“钉尖向上”的频率总在某个数字附近,显示出一定的稳定性,可以估计“钉尖向上”的概率是( )
A、 B、 C、 D、10. 如图显示了用计算机模拟随机投掷一枚图钉的实验结果.随着试验次数的增加,“钉尖向上”的频率总在某个数字附近,显示出一定的稳定性,可以估计“钉尖向上”的概率是( )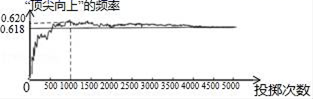 A、0.620 B、0.618 C、0.610 D、100011. 如图,AB是⊙O的直径,弦CD⊥AB于点G.点F是CD上一点,且满足 ,连接AF并延长交⊙O于点E.连接AD、DE,若CF=2,AF=3.给出下列结论:
A、0.620 B、0.618 C、0.610 D、100011. 如图,AB是⊙O的直径,弦CD⊥AB于点G.点F是CD上一点,且满足 ,连接AF并延长交⊙O于点E.连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E= ;④S△DEF=4 .
其中正确的是( )
 A、①②④ B、①②③ C、②③④ D、①③④12. 二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:
A、①②④ B、①②③ C、②③④ D、①③④12. 二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:();();();()若点 , 点 , 点在该函数图象上,则;()若方程的两根为和 , 且 , 则 .
其中正确的结论有( )
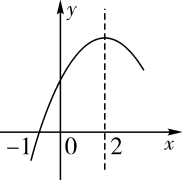 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(共5题,共20分)
-
13. 设 、 是方程 的两个实数根,则 的值为 .14. 如图,在△BDE中,∠BDE=90°, BD=4,点D的坐标是( 6,0) ,∠BDO=15°,将 BDE 旋转到 △ABC的位置,点C 在 BD上,则旋转中心的坐标为 .
 15. 在一个不透明的口袋中装有5个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在0.25附近,则估计口袋中白球大约有个.16. 如图, 内接于 , , 的角平分线交 于 . 若 , , 则 的长为 .
15. 在一个不透明的口袋中装有5个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在0.25附近,则估计口袋中白球大约有个.16. 如图, 内接于 , , 的角平分线交 于 . 若 , , 则 的长为 . 17. 如图,在平面直角坐标系 中,已知抛物线 的顶点为 , 与 轴的正半轴交于点 , 它的对称轴与抛物线 交于点 . 若四边形 是正方形,则 的值是 .
17. 如图,在平面直角坐标系 中,已知抛物线 的顶点为 , 与 轴的正半轴交于点 , 它的对称轴与抛物线 交于点 . 若四边形 是正方形,则 的值是 .
三、解答题(共4题,共52分)
-
18. 为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,小莹随机抽查了所住小区 户家庭的月用水量,绘制了下面不完整的统计图.
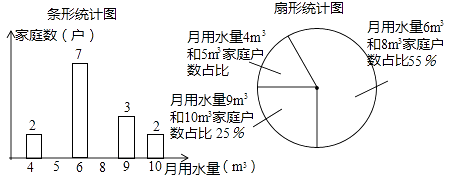 (1)、求 并补全条形统计图;(2)、求这 户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;(3)、从月用水量为 和 的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为 和 恰好各有一户家庭的概率.19. 如图,已知是的直径, , 是上的点, , 交于点 , 连接 .
(1)、求 并补全条形统计图;(2)、求这 户家庭的月平均用水量;并估计小莹所住小区420户家庭中月用水量低于月平均用水量的家庭户数;(3)、从月用水量为 和 的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为 和 恰好各有一户家庭的概率.19. 如图,已知是的直径, , 是上的点, , 交于点 , 连接 . (1)、求证:;(2)、若 , , 求的长.20. 为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加,某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量(千克)与销售价(元/千克)有如下关系: . 设这种产品每天的销售利润为元.(1)、求与之间的函数关系式.并指出该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?(2)、如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?21. 如图1,抛物线与轴交于点和点 , 与轴交于点 , 抛物线的顶点为 , 轴于点 . 将抛物线平移后得到顶点为且对称轴为直线的抛物线 .
(1)、求证:;(2)、若 , , 求的长.20. 为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加,某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量(千克)与销售价(元/千克)有如下关系: . 设这种产品每天的销售利润为元.(1)、求与之间的函数关系式.并指出该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?(2)、如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?21. 如图1,抛物线与轴交于点和点 , 与轴交于点 , 抛物线的顶点为 , 轴于点 . 将抛物线平移后得到顶点为且对称轴为直线的抛物线 .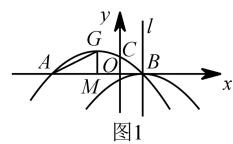
 (1)、求抛物线的解析式;(2)、如图2,在直线上是否存在点 , 使是等腰三角形?若存在,请求出所有点的坐标;若不存在,请说明理由;(3)、点为抛物线上一动点,过点作轴的平行线交抛物线于点 , 点关于直线的对称点为 . 若以 , , 为顶点的三角形与全等,求直线的解析式.
(1)、求抛物线的解析式;(2)、如图2,在直线上是否存在点 , 使是等腰三角形?若存在,请求出所有点的坐标;若不存在,请说明理由;(3)、点为抛物线上一动点,过点作轴的平行线交抛物线于点 , 点关于直线的对称点为 . 若以 , , 为顶点的三角形与全等,求直线的解析式.