陕西省延安市洛川县2022-2023学年七年级上学期期末数学试卷

试卷更新日期：2023-02-14 类型：期末考试

进入出卷网下载

一、选择题（共8小题，每小题3分，计24分.）

1. ﹣ $\frac{1}{2}$ 的相反数是（）

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、﹣2 D、2

查看试题解析
2. 下面的几何体中，哪一个不能由平面图形绕某直线旋转一周得到（）

A、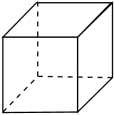 B、 C、 D、

查看试题解析
3. 若∠A＝50°，则∠A的补角为（）

A、40° B、50° C、120° D、130°

查看试题解析
4. 2021年5月22日，中国工程院院士袁隆平在长沙不幸逝世.这位“共和国勋章获得者”的最大贡献是杂交水稻技术.2020年我国水稻种植面积4.5亿亩，其中50%左右是杂交水稻，则杂交水稻种植面积用科学记数法表示约为（）

A、 4.5×10⁸亩 B、2.25×10⁸亩 C、4.5×10⁹亩 D、2.25×10⁹亩

查看试题解析
5. 下面计算正确的是（）

A、3x²y-2y²x＝xy B、 $a b - \frac{b a}{2} = \frac{1}{2} a b$ C、2a²+a＝3a³ D、m⁴+m⁴＝m⁸

查看试题解析
6. 若☆是规定的运算符号，设a☆b＝ab+a+b，则在3☆x＝-9中，x的值是（）

A、3 B、-3 C、4 D、-4

查看试题解析
7. 已知A，B，C是同一直线上的三个点，且AB＝9cm，BC＝4cm，D是BC的中点，则AD的长是（）

A、13cm B、7cm C、11cm D、7cm或11cm

查看试题解析
8. 已知x+2y＝7，4m-3n＝8，则代数式（9n-4y）-2（6m+x）+3的值为（）

A、38 B、35 C、-35 D、-32

查看试题解析

二、填空题（共5小题，每小题3分，计15分）

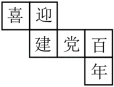
9. 计算：25°45′+62°19′＝．

查看试题解析
10. 已知x＝1是关于x的方程2x+m＝6的解，则m的值为．

查看试题解析
11. 某正方体的每一个面上都有一个汉字，它的一种表面展开图如图所示，那么在原正方体中，与“喜”字所在面相对面上的汉字是．

查看试题解析
12. A、B、C三点在数轴上的位置如图所示，则-a、b、-c的大小关系．

查看试题解析
13. 如图，这是由相同大小的正方形和相同大小的圆按照一定规律摆放而成的，按此规律，则第（n）个图形中圆的个数为.

查看试题解析

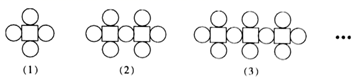
三、解答题（共13小题，计81分）

14. 计算： ${(- 1)}^{2} - \frac{9}{5} \div (- \frac{3}{25}) - | - 7 |$

查看试题解析
15. 解方程： $\frac{4 x - 1}{6} = 1 - \frac{3 x - 1}{2}$ ．

查看试题解析
16. 先化简，再求值：3（x²-2xy）-[x²-3y+3（xy+y）]，其中x＝-2，y＝ $\frac{1}{3}$ ．

查看试题解析
17. 已知a，b互为倒数，c，d互为相反数（c≠0），|m|＝3，求 $\frac{m}{3} - a b + \frac{c + d}{5} - \frac{c}{d}$ 的值．

查看试题解析
18. 如图，已知直线l和直线外A，B，C三点，按下列要求画图：

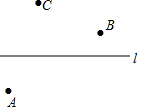
⑴画射线AB；

⑵连接BC，延长BC至点D使得CD＝BC；

⑶在直线l上确定点E，使得点E到点A，点C的距离之和最短．

查看试题解析
19. 如图，是一个由5个正方体组成的立体图形，分别从正面、左面、上面观察这个立体图形，各能得到什么平面图形？请你在网格上画出来．

查看试题解析
20. 已知单项式2x^2my⁷与单项式5x⁶yⁿ⁺⁸是同类项，求m²+2n的值．

查看试题解析
21. 《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八，盈三；人出七，不足四，问物价几何？译文为：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元，问这个物品的价格是多少元？

查看试题解析
22. 如图，在一条不完整的数轴上从左到右有点A，B，C，其中AB＝2，BC＝1，设点A，B，C所对应数的和是m．若以B为原点，求出点A，C所对应的数，并计算m的值；若以C为原点，m又是多少？

查看试题解析
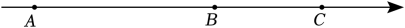23. 为了庆祝中华人民共和国成立72周年，空军航空开放活动在其机场举行，某特技飞行队做特技表演时，其中一架J31型飞机起飞0.5km后的高度（上升记为正）变化为：+2.5km，-1.2km，+1.1km，-1.4km．

(1)、求该飞机完成这四个表演动作后离地面的高度；

(2)、已知飞机平均上升1km需消耗5L燃油，平均下降1km需消耗3L燃油，那么这架飞机在做完这四个表演动作过程中，一共消耗了多少升燃油？

查看试题解析
24. 如图，C是线段AB上一点，M，N分别是AC，BC的中点．

(1)、若AC＝8cm，BC＝6cm，求线段MN的长；

(2)、若线段CM与线段CN的长度之比为2：1，且线段CN＝4cm，求线段AB的长．

查看试题解析
25. 某商场计划投入一笔资金（即本金）采购一批商品，经过市场调查发现，有两种销售方式：
方式A：若月末出售，可获利30%，但要支付仓储费用600元；
方式B：若月初出售，可获利20%，并可用本金和利润再投资其他商品，到月末又可获利5%．若商场投资本金x元．

(1)、分别用含x的最简代数式表示出按方式A，B出售所获得的利润；

(2)、若商场投资本金30000元，选择哪种销售方式获利较多？并求出此时获利金额．

查看试题解析
26. 已知点O是直线AB上一点，过O作射线OC，使∠BOC＝110°．

(1)、如图①，∠AOC＝；

(2)、如图②，过点O作射线OD使∠COD＝90°，作∠AOC的平分线OE，求∠DOE的度数；

(3)、在（2）的条件下，作射线OF，若∠BOF与∠AOE互余，画出图形，并求出∠DOF的度数．

查看试题解析